Generalized Payment as Types

A Toy Model/Specification for Superfluid Money Concepts

Miao, ZhiCheng, Co-founder of Superfluid Finance

What You Will Hear About

A new payment paradigm:
- where money can be instantly or continuously moved from 1-to-1 or 1-to-N en-mass.
How a Haskell toy model/reference implementation/specification for it is written:
- Haskell - A pure, strongly-typed, syntactically terse language best suited for domain modeling.
- "A domain model is a conceptual model of the domain that incorporates both behavior and data."
- Also similar to what Conal Elliot advocated for: a denotational design of software.
A teaser of new perspectives on money,
- Let's search for some categories related to money.
- Real time finance, a new area for innovations.

Rethinking The Domain of Payment

Some Payment Requests

Instant

Bob requests to send €42 to Alice now.

Streaming

Bob requests to send a constant flow of money at €420 per 30 day to Alice now.

Instant en mass

Microsoft requests to send $0.42 per share to all its share holders on the next ex-dividend date.

Streaming en mass

Elon Musk requests to send a constant flow of money at €4.2B per 360 days to all its share holders with individual flow rates proportional to their number of share units, from 20st April.

Existing Systems

Financial Market Utilities (FMUs): SEPA, TARGET2, Fedwire, CHIPS, SWIFT, etc. ¹
Public Blockchains and their token standards: Bitcoin, Ethereum, Ethereum ERC-20 tokens, etc.

Feature Comparison of Existing Systems

	FMUs	Public blockchain
Instant	Yes, fast within the system, poor interoperability	Yes, with scalability issue
Streaming	Micro transactions	Micro transactions, but can be costly on some system
en mass	NOPE	Some system may have ad-hoc implementations.

An Ideal System

FORMAL SPECIFICATION
- A foundation designed using denotational semantics approach. (Conal Elliott/Lambda Jam 2015)
- Built with compositionality in mind. (Simon Peyton Jones/Microsoft research, "Composing contracts")
EFFICIENT
- A system that interprets the DSL and performs the operations with as little as possible information waste.
  - Use micro payments to simulate flow of money? NOPE
  - Send dividens payment one by one to all share holders? NOPE
  - They are all too noisy.

What We Should Build

Design an denotational semantics for new payment requests.
An expressive and composable DSL for the semantics.
A new payment rail that natively interprets and execute the DSL.

Designing Payment Semantics in Layers

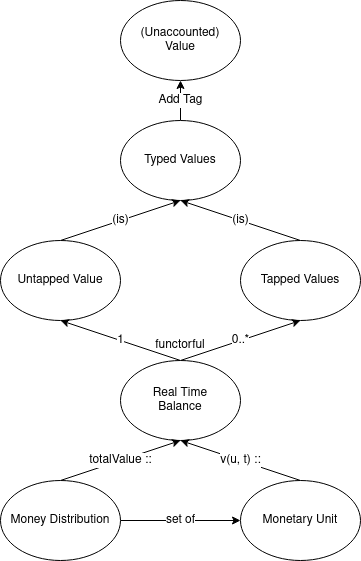
Money at Syntactic Level

How money is represented in the system?

(Unaccounted) Value

class (Integral v, Default v) => Value v

But there are no further "types" of value.
Let us call these values unaccounted for.

Typed Values

We give value a tag, so that it can be accounted for by sub systems.
We will see what are sub systems later…

-- | Typed value is an otherwise unaccounted value ~v~ with an associated ~vtag~.
class ( TypedValueTag vtag
      , Value v
      ) => TypedValue tv vtag v | tv -> v, tv -> vtag where
    untypeValue :: tv -> v
    default untypeValue :: Coercible tv v => tv -> v
    untypeValue = coerce

-- | Tag for typed value type class using ~Typeable~ runtime information.
class Typeable vtag => TypedValueTag vtag where
    tappedValueTag :: Proxy vtag -> String

Tapped and Untapped Values

There are two sub classes of typed values:
- Untapped typed value doesn't have a designated sub system. Hence any sub system can add or remove amount of this type.
- Any tapped typed value on the other hand is designed to a specific sub system. Hence only that sub system can add or remove amount of this type.
- An example is that, in your personal account, untapped typed value is what you can still use, while tapped typed value is what is reserved by the bank for a future transaction.

Code

  -- | Untapped value type. It can be freely accessed by any sub systems.
  newtype UntappedValue v = UntappedValue
  instance Value v => TypedValue (UntappedValue v) UntappedValueTag v

  -- | Tapped value tag. It must only be accessed by its designated sub system.
  class TypedValueTag tvtag => TappedValueTag tvtag
  instance (Value v, TypedValueTag vtag) => TypedValue (TappedValue vtag v) vtag v

Real Time Balance

Let's call a functorful of these typed value RealTimeBalance.
Or simply view it is a list of typed values [untapped value, tapped value 1, tapped value 2, ...].

class ( Value v
      , Foldable rtbF
      , Monoid (rtbF v)
      ) => RealTimeBalance rtbF v | v -> rtbF where

    -- | Convert a single monetary value to a RTB value.
    valueToRTB :: v -> rtbF v

    -- | Net monetary value of a RTB value.
    netValueOfRTB :: rtbF v -> v
    netValueOfRTB = foldr (+) def

    -- | Convert typed values to a RTB value.
    typedValuesToRTB :: UntappedValue v -> [AnyTappedValue v] -> rtbF v

    -- | Get typed values from a RTB value.
    typedValuesFromRTB :: rtbF v -> (UntappedValue v, [AnyTappedValue v])

Real Time Balance Properties

-- monoid laws
monoid_right_identity    x = (x <> mempty) `sameAs` x
monoid_left_identity     x = (mempty <> x) `sameAs` x
monoid_associativity a b c = ((a <> b) <> c) `sameAs` (a <> (b <> c))
-- in addition to monoid laws, it also has some other nice properties:
monoid_mappend_commutativity          a b =
    (a <> b) `sameAs` (b <> a)
rtb_identity_from_and_to_typed_values   x = -- type of x is a RealTimeBalance
    (uncurry typedValuesToRTB . typedValuesFromRTB) x `sameAs` x
rtb_conservation_of_net_value           x = -- type of x is a Value
    (netValueOfRTB . valueToRTB) x == x

Money Distribution & Monetary Units (Current Theory)

U is the set of monetary units.
ν : U → N is the value function.
β : U → B is the bearer function.
Monetary unit examples: coins, bank notes, bank account, crypto wallet, etc.

Cit. buldas2021unifying - A Unifying Theory of Electronic Money and Payment Systems

Superfluid's Money Distribution & Money Units

ν needs an additional input ctx, known as the context.
ctx should be some value that's "shared" globally in nature.
For example, it could be timestamp.
Further more, ν returns a RTB instead of the unaccounted value type.

Review: how money is represented in the system

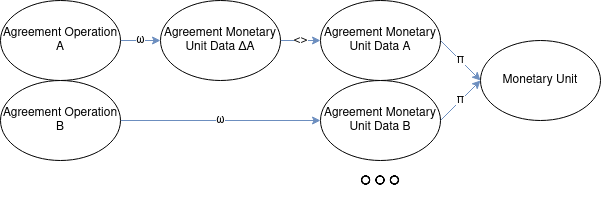
Money at Semantic Level

How money should be moved in the system?

Agreement Framework

Let us define another concept "agreement", to represent on-going relationships between monetary units.
It has two parts:
- Agreement Monetary Unit Data.
- Agreement Operation.

Agreement Monetary Unit Data

It provides part of the real time balance for the monetary unit.

class ( SuperfluidTypes sft
      , Monoid amud -- !! A MONOID, so that system may scale
      ) => AgreementMonetaryUnitData amud sft | amud -> sft where
    -- | π function -
    --   balance provided (hear: π) by the agreement monetary unit data.
    balanceProvidedByAgreement
        :: amud          -- amud
        -> SFT_TS sft    -- t !! THIS IS WHAT MAKES THINGS REAL TIME
        -> SFT_RTB sft   -- rtb

-- | Calculate the real time balance of an monetary unit at a given time.
balanceOfAt :: (SuperfluidTypes sft, MonetaryUnit mu sft)
    => mu -> SFT_TS sft -> SFT_RTB sft
balanceOfAt mu t = foldr -- !! THIS IS THE: ν(u, t)
    -- !! providedBalanceByAnyAgreement is the balanceProvidedByAgreement for the existential type
    --    returned from agreementsOf.
    ((<>) . (flip (providedBalanceByAnyAgreement mu) t))
    mempty
    (agreementsOf mu)

Agreement Operations

They are the little engines that make values move.

class ( SuperfluidTypes sft
      , AgreementMonetaryUnitData (AgreementMonetaryUnitDataInOperation ao) sft
      ) => AgreementOperation ao sft | ao -> sft where
    -- ... for brevity, removed some type definitions here...

    -- | ω function - apply agreement operation ~ao~ (hear: ω) onto the agreement
    --   operation data ~aod~ to get a tuple of:
    --
    --   1. An updated ~aod'~.
    --   2. A functorful delta of agreement monetary unit data ~aorΔ~, which then
    --      can be monoid-appended to existing ~amud~. This is what can make an
    --      agreement scalable.
    applyAgreementOperation
        :: amud ~ (AgreementMonetaryUnitDataInOperation ao)
        => ao                                   -- ao
        -> AgreementOperationData ao            -- aod
        -> SFT_TS sft                           -- t
        -> ( AgreementOperationData ao
           , AgreementOperationResultF ao amud) -- (aod', aorΔ)

Review: Agreement Framework

Instant Transfer Agreement (ITA)

Semantic: Party A sends an X amount of money instantly to party B.

ITA's Monetary Unit Data

Built from lenses.
TLDR: Lens' is a data structure of a pair of getter and setter.

class (Default amuLs, SuperfluidTypes sft)
    => MonetaryUnitLenses amuLs sft | amuLs -> sft where
    untappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft))

ITA's ω Function

newtype Operation sft = Transfer (SFT_MVAL sft)

instance SuperfluidTypes sft => AgreementOperation (Operation sft) sft where
    data AgreementOperationResultF (Operation sft) elem = OperationPartiesF
        { transferFrom :: elem
        , transferTo   :: elem
        } deriving stock (Functor, Foldable, Traversable)

    applyAgreementOperation (Transfer amount) acd _ = let
        acd'  = acd
        aorΔ = fmap ITMUD.MkMonetaryUnitData (OperationPartiesF
                    (def & set ITMUD.untappedValue (coerce (- amount)))
                    (def & set ITMUD.untappedValue (coerce    amount)))
        in (acd', aorΔ)

ITA's Monetary Unit Data Monoid & π function

monoid

instance MonetaryUnitLenses amuLs sft
    => Semigroup (MonetaryUnitData amuLs sft) where
    (<>) (MkMonetaryUnitData a) (MkMonetaryUnitData b) =
        let c = a & over untappedValue (+ b^.untappedValue)
        in MkMonetaryUnitData c
instance MonetaryUnitLenses amuLs sft
    => Monoid (MonetaryUnitData amuLs sft) where
    mempty = MkMonetaryUnitData def

π function

instance MonetaryUnitLenses amuLs sft
    => AgreementMonetaryUnitData (MonetaryUnitData amuLs sft) sft where
    balanceProvidedByAgreement (MkMonetaryUnitData a) _ =
        typedValuesToRTB (a^.untappedValue) []

ITA in Action

SF.transfer uses the ITA.Operation defined above, this is how its semantic looks like:

runToken token $ SF.transfer (ITA.OperationPartiesF bob alice) (USD 42)

Well, we just redefined 1to1 instant payment using this new semantic… big deal, what's next?

Constant Flow Agreement (CFA)

Semantic: Party A sends a flow of money at a constant rate X to party B.

How can it work in a nut shell?
- A and B shares the same context "time", when time advances A & B's balances move at the same rate but opposite direction for both of them, for one single CFA agreement.
- Any party can have as many such CFA agreements on going as needed, its all in one single value: net flow rate for the party. Thanks to the monoid structure, it is very scalable.

CFA's Monetary Unit Data

class (Default amuLs, SuperfluidTypes sft)
    => MonetaryUnitLenses amuLs sft | amuLs -> sft where
    settledAt            :: Lens' amuLs (SFT_TS sft)
    settledUntappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft))
    netFlowRate          :: Lens' amuLs (SFT_MVAL sft)
instance MonetaryUnitLenses amuLs sft
    => Semigroup (MonetaryUnitData amuLs sft) where
    (<>) (MkMonetaryUnitData a) (MkMonetaryUnitData b) =
        let c = a & set  settledAt            (  b^.settledAt)
                  & over settledUntappedValue (+ b^.settledUntappedValue)
                  & over netFlowRate          (+ b^.netFlowRate)
        in MkMonetaryUnitData c

CFA's π Function

instance MonetaryUnitLenses amuLs sft
    => AgreementMonetaryUnitData (MonetaryUnitData amuLs sft) sft where
    balanceProvidedByAgreement (MkMonetaryUnitData a) t = typedValuesToRTB
            ( UntappedValue $ uval_s + fr * fromIntegral (t - t_s) ) []
        where t_s                  = a^.settledAt
              UntappedValue uval_s = a^.settledUntappedValue
              fr                   = a^.netFlowRate

CFA's ω Function

-- ... some defintions are omitted for brevity ...
applyAgreementOperation (UpdateFlow newFlowRate) acd t' = let
  acd' = ContractData { flow_last_updated_at = t'
                      , flow_rate   = newFlowRate
                      }
  aorΔ = OperationPartiesF
           (def & set CFMUD.settledAt t'
                & set CFMUD.netFlowRate          (-flowRateΔ)
                & set CFMUD.settledUntappedValue (UntappedValue $ -settledΔ)
           )
           (def & set CFMUD.settledAt t'
                & set CFMUD.netFlowRate           flowRateΔ
                & set CFMUD.settledUntappedValue (UntappedValue settledΔ)
           )
  in (acd', fmap CFMUD.MkMonetaryUnitData aorΔ)
  where t         = flow_last_updated_at acd
        fr        = flow_rate acd
        settledΔ  = fr * fromIntegral (t' - t) -- !! KEY equition
        flowRateΔ = newFlowRate - fr

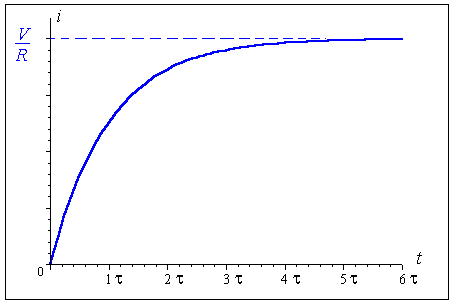
Decaying Flow Agreement (DFA)

Semantic: Party A sends a flow of money at a decaying rate Λ to party B with a distribution limit of X.

For recipient looks like receiving money over a decaying curve (with a half-life determined by Λ):

DFA's π Function:

    balanceProvidedByAgreement (MkMonetaryUnitData a) t = typedValuesToRTB
            ( UntappedValue $ ceiling $ α * exp (-λ * t_Δ) + ε ) []
        where t_s   = a^.settledAt
              α     = a^.αVal
              ε     = a^.εVal
              λ     = a^.decayingFactor
              t_Δ   = fromIntegral (t - t_s)

Similar to CFA it is scalable, but only for the same Λ value.

Indexes for Lenses

Challenge: How to augment previously mentioned semantics with 1 to N proportional distribution semantic?

Lenses come to the rescue.
Indexes are where the actual lenses are provided.

A reminder, lenses for the ConstantFlow:

  class (Default amuLs, SuperfluidTypes sft)
      => MonetaryUnitLenses amuLs sft | amuLs -> sft where
      settledAt            :: Lens' amuLs (SFT_TS sft)
      settledUntappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft))
      netFlowRate          :: Lens' amuLs (SFT_MVAL sft)

Constant Flow Family

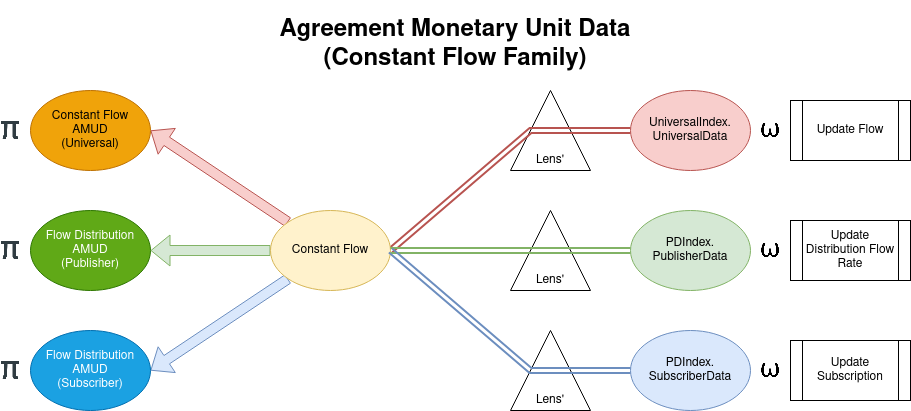
Universally Indexed Lenses

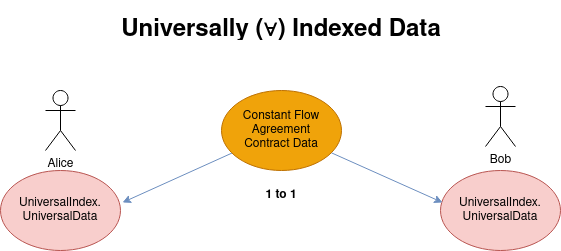
For all (∀, universal) monetary unit data there exists one and only one set of universal lenses.
As a result, combining ConstantFlow and universal indexed lenses gives you the 1to1 semantic agreements:
- Instant Transfer Agreement (ITA)
- Constant Flow Agreement (CFA)
- Decaying Flow Agreement (DFA)
- etc.

Universal Index for Constant Flow

data UniversalData sft = UniversalData -- UniversalMonetaryUnitData
    { -- ...
    , cfa_settled_at             :: SFT_TS sft
    -- ...

-- | Monetary unit lenses for the universal index.
instance SuperfluidTypes sft => CFMUD.MonetaryUnitLenses (UniversalData sft) sft where
    settledAt            = $(field 'cfa_settled_at)
    settledUntappedValue = $(field 'cfa_settled_untapped_value)
    netFlowRate          = $(field 'cfa_net_flow_rate)

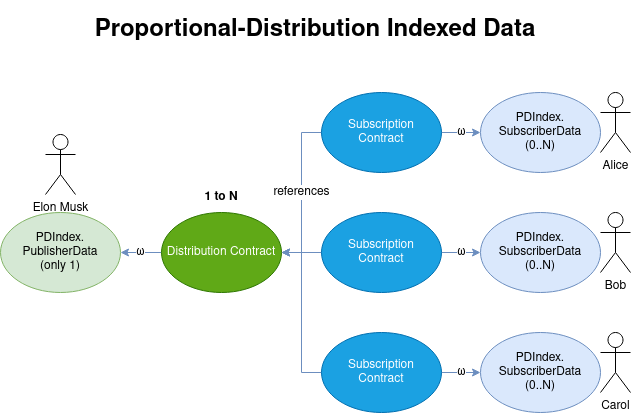
Proportional Distribution Indexed Lenses

A publisher owns a distribution.
Each distribution can have any number of subscribers.
Each subscriber owns a number of units in the distribution.
Subscribers can receive money distributions from the publisher proportionally per their number of units.

Proportional Distributions Index for Constant Flow

Constant Flow Distribution Agreement.

Review: How money is moved in the system

Sub systems created through "agreement framework" have:

π function - providing a portion of real time balance to the monetary unit data value function, with time also part of its input.
ω function - transforming data or create agreement monetary unit data delta monoids that affect the inputs to the π function.
Lens abstraction - A optional technique to compose smaller building blocks for 1to1 and 1toN proportional distribution semantics.

Review: Notable Agreements

Instant Transfer Agreement (payment as we are familiar with)
Constant Flow Agreement (1to1 constant money flows)
Decaying Flow Agreement (1to1 decaying money flow with a distribution limit and a half-life of flow rate)
Instant Distribution Agreement (1toN instant transfer)
Constant Flow Distribution Agreement (1toN constant money flows)

Money at Pragmatic Level

How to have compositionality and add context to the system?

DISCLAIMER: Not everything mentioned here is implemented in the spec yet, but we will show the working Haskell code that demonstrates the main idea.

Contract Representation

-- simplified for brevity
class AgreementOperationWithData a where
  runAgreement :: a -> IO ()
data PaperAgreement = MkPaperAgreement String
instance AgreementOperationWithData PaperAgreement where
  runAgreement (MkPaperAgreement s) = putStrLn s
-- | A contract executable within the IO monad context.
data Contract = Contract
  { contractPreCond      :: IO Bool
  , contractExecs        :: [AnyAgreementOperationWithData]
  , contractAttachedCond :: (IO Bool, AnyAgreementOperationWithData)
  }
-- Define an existential type to avoid an explicit sum type...
data AnyAgreementOperationWithData = forall a.
  AgreementOperationWithData a => MkAnyAOD a
instance AgreementOperationWithData AnyAgreementOperationWithData where
  runAgreement (MkAnyAOD a) = runAgreement a

A Toy Contract Execution Engine

data Contract = Contract
  { contractPreCond      :: IO Bool
  , contractExecs        :: [AnyAgreementOperationWithData]
  , contractAttachedCond :: (IO Bool, AnyAgreementOperationWithData)
  }

execContract :: Contract -> IO ()
execContract (Contract preCond execs _) = do
  pred <- preCond
  if pred then mapM_ runAgreement execs
    else putStrLn "No bueno, amigo"

execCondContract :: Contract -> IO ()
execCondContract (Contract _ _ (cond, a)) = do
  pred <- cond
  if pred then runAgreement a
    else putStrLn "No tan rápida, amigo"

Testing the Toy Contract Execution Engine

main = do
  brrr <- newIORef False
  let sec_says_no = return False
  let sec_says_yes = return True
  let when_money_goes_brrr = readIORef brrr
  let c0 = Contract
           sec_says_no
           [ MkAnyAOD $ (MkPaperAgreement "Elon Musk buys Twitter") ]
           (return False, MkAnyAOD $ MkPaperAgreement "Not possible")
  let c1 = Contract
           sec_says_yes
           [ MkAnyAOD $ MkPaperAgreement "Bob sends Alice $42 dollar"
           , MkAnyAOD $ MkPaperAgreement "Alice sends Carol $4.2 dollar"
           ]
           ( when_money_goes_brrr,
             MkAnyAOD $ MkPaperAgreement "Alice pays Bob back $420 dollars" )

Testing Result

  putStrLn "# Contract 0"
  execContract c0

  putStrLn "# Contract 1"
  execContract c1
  execCondContract c1

  putStrLn "Money goes brrr..."
  writeIORef brrr True
  execCondContract c1

# Contract 0
No bueno, amigo
# Contract 1
Bob sends Alice $42 dollar
Alice sends Carol $4.2 dollar
No tan rápida, amigo
Money goes brrr...
Alice pays Bob back $420 dollars

An Example from "Composing Contracts"

"How to write a financial contract" by Simon Peyton Jones & Microsoft Research.

European option: at a particular date you may choose to acquire an “underlying” contract, or to decline

or :: Contract -> Contract -> Contract
-- Acquire either c1 or c2 immediately

zero :: Contract
-- A worthless contract

european :: Date -> Contract -> Contract
european t u = at t (u `or` zero)

Money at Dynamic Level

Money at dynamic level has "potential to update its context".

Let There be Side Effects

Let side effects make money useful!
We already see the toy example using IO monad, in real implementation these are needed side effects:
- Load data from storage.
- Read context such as time.
- Authentication (Blockchain digital signature).
- Authorization (Who can update whose agreement?).
- Atomic transaction, for composed contract.
- …

Token as a Monad

class ( Monad tk
      , SuperfluidTypes sft
      , Account acc sft
      ) => Token tk acc sft | tk -> acc, tk -> sft where
    balanceOfAccount :: ACC_ADDR acc -> tk (SFT_RTB sft)
    transfer :: CONTRACT_ACC_ADDR acc (ITA.Operation sft) -> SFT_MVAL sft -> tk ()
    updateFlow :: CONTRACT_ACC_ADDR acc (CFA.Operation sft) -> CFA.FlowRate sft -> tk ()
    -- ...
    distributeProportionally
        :: ACC_ADDR acc                    -- publisher
        -> ProportionalDistributionIndexID -- indexId
        -> SFT_MVAL sft                    -- amount
        -> tk ()
    -- ...

Token is like a bank, and it manages accounts.
But note can be modeled similarly too as an monad!
Choose effect systems: mtl, transformers, free monads, polysemy.

Implementations & Plans

Superfluid Protocol EVMv1 Implementation

Early Superfluid Protocol idea is implemented for EVM blockchains in Solidity language.
Not all the denotational semantics have been implemented.
Live in production: Polygon, Gnosis Chain, Optimism, Arbitrum, Avalanche, BSC.
Achieved stats: >= 30K addresses, >= $10M streamed a month.

Haskell Specification for Superfluid Protocol

Still work in progress, but already functional.
Plan to fully support and prototype new denotational semantics for payment.
Plan to also work on financial contract combinators, inspired by Simon Peyton Jones' "Composing contracts" paper².

Money and its Categories

About Category Theory, Some Quotes

"Here's a categorical rule of thumb: every time you have composition, you should look for a category."

Bartosz Milewski

"Category theory is the study of compositionality: building big things out of little things, preserving guarantees."

Ken Scambler

"Programmer's search of compositionality."

Victor Frankl
~~Victor Frankl~~ /jk

The Dark Side: "Category theorists are intellectual terrorists."

Philip Wadler

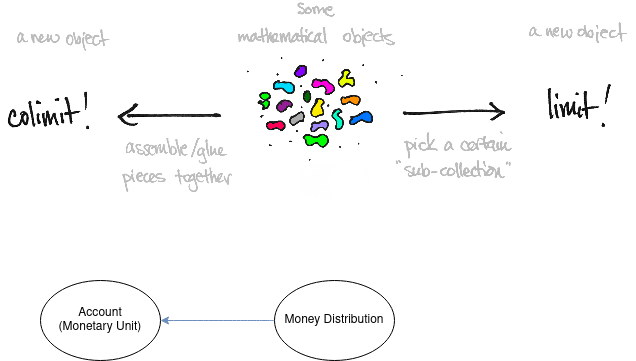
Category of Money Distribution

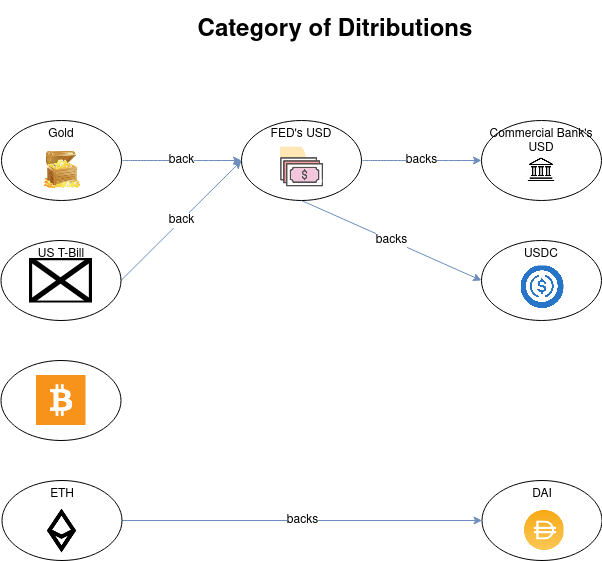
From Monetary Distribution to Monetary Unit Data

Limit / Colimit.

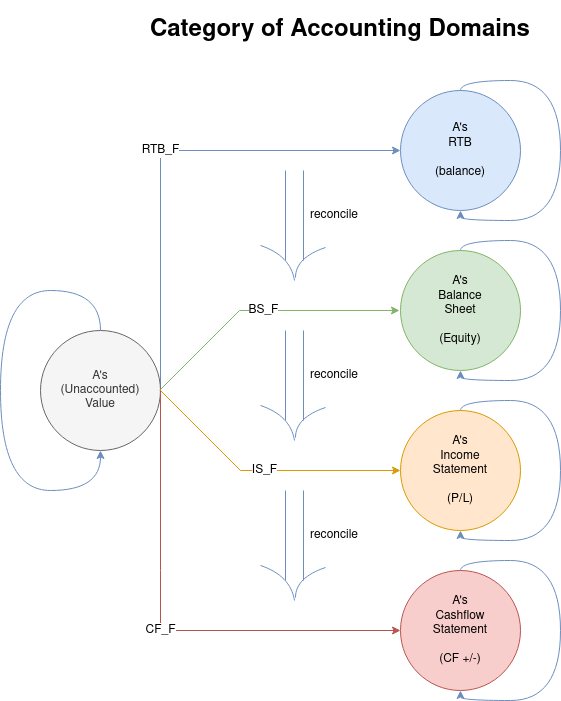
Category of Accounting Domain

Real Time Finance:

Real Time Payment - A money distribution where the value of each monetary unit in it is also a function of time.
Compositionaility - The morphism of the money distribution are composed financial contracts.
Real Time Accounting - Natural transformations between different accounting domains (RTB of Account, Balance Sheet, Income Statement, Cashflow Statement, etc.)

Date	Notes
2022-07-13	First quick draft for guardtime visit
2022-07-29	Re-drated for the lambda days 2022