Scheme_Taylor2 class

Contents

Description

This is a sub-class of the Scheme class for the implementation of the time integration scheme Taylor 2nd Order.

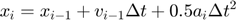
$$x_{i} = x_{i-1} + v_{i-1} \Delta t + 0.5 a_{i} \Delta t^{2}$$

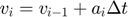
$$v_{i} = v_{i-1} + a_{i} \Delta t$$

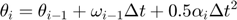
$$\theta_{i} = \theta_{i-1} + \omega_{i-1} \Delta t + 0.5 \alpha_{i} \Delta t^{2}$$

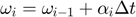
$$\omega_{i} = \omega_{i-1} + \alpha_{i} \Delta t$$

Notation:

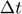$\Delta t$: Time increment

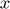$x$: Coordinates

$v$: Translational velocity

$a$: Translational acceleration

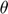$\theta$: Angular orientation

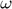$\omega$: Angular velocity

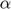$\alpha$: Angular acceleration

classdef Scheme_Taylor2 < Scheme

Constructor method

    methods
        function this = Scheme_Taylor2()
            this = this@Scheme(Scheme.TAYLOR_2);
        end
    end

Public methods: implementation of super-class declarations

    methods
        %------------------------------------------------------------------
        function updatePosition(~,p,dt)
            p.coord     = p.coord     + p.veloc_trl * dt + 0.5 * p.accel_trl * dt^2;
            p.veloc_trl = p.veloc_trl + p.accel_trl * dt;
        end

        %------------------------------------------------------------------
        function updateOrientation(~,p,dt)
            p.orient    = p.orient    + p.veloc_rot * dt + 0.5 * p.accel_rot * dt^2;
            p.veloc_rot = p.veloc_rot + p.accel_rot * dt;
        end

        %------------------------------------------------------------------
        function updateTemperature(~,~,~)
            % Not available
        end
    end

end


Published with MATLAB® R2019b