ContactForceT_DashpotSlider class

Contents

Description

This is a sub-class of the ContactForceT class for the implementation of the Dashpot-Slider tangent contact force model.

This model assumes that the tangent contact force has a viscous component 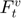$F_{t}^{v}$, provided by a linear dashpot, and a friction component 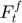$F_{t}^{f}$, provided by a slider, which limits the total force according to Coulomb law.

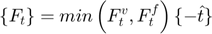
$$\left \{ F_{t} \right \} = min\left ( F_{t}^{v},F_{t}^{f} \right ) \{-\hat{t}\}$$

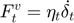
$$F_{t}^{v} = \eta_{t} \dot{\delta_{t}}$$

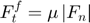
$$F_{t}^{f} = \mu \left | F_{n} \right |$$

The tangent damping coefficient 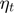$\eta_{t}$ and the friction coefficient 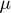$\mu$ must be provided.

Notation:

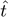$\hat{t}$: Tangent direction between elements

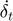$\dot{\delta_{t}}$: Time rate of change of tangent overlap

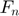$F_{n}$: Normal contact force vector

References:

classdef ContactForceT_DashpotSlider < ContactForceT

Public properties

    properties (SetAccess = public, GetAccess = public)
        % Contact parameters
        damp double = double.empty;   % damping coefficient
        fric double = double.empty;   % friction coefficient
    end

Constructor method

    methods
        function this = ContactForceT_DashpotSlider()
            this = this@ContactForceT(ContactForceT.DASHPOT_SLIDER);
            this = this.setDefaultProps();
        end
    end

Public methods: implementation of super-class declarations

    methods
        %------------------------------------------------------------------
        function this = setDefaultProps(this)

        end

        %------------------------------------------------------------------
        function this = setCteParams(this,~)

        end

        %------------------------------------------------------------------
        function this = evalForce(this,int)
            % Force modulus (viscous and friction contributions)
            fv = this.damp * int.kinemat.vel_t;
            if (~isempty(int.cforcen))
                ff = this.fric * norm(int.cforcen.total_force);
            else
                ff = 0;
            end

            % Limit elastic force by Coulomb law
            f = min(abs(fv),abs(ff));

            % Total tangential force vector (against deformation and motion)
            this.total_force = -f * int.kinemat.dir_t;
        end
    end

end


Published with MATLAB® R2019b