ConductionIndirect_VoronoiA class

Contents

Description

This is a sub-class of the ConductionIndirect class for the implementation of the Voronoi Polyhedra A indirect heat conduction model.

This model assumes that the indirect heat conduction between two neighboring elements is restricted to the region delineated by the double pyramid whose apexes are the particles' centers and base is the Voronoi boundary plane shared by the particles' cells. For simplicity, the double pyramid is treated as a double tapered cone with the same base area A. In 2D, the Voronoi edge shared by the cells of both particles represents the diameter of the cone base.

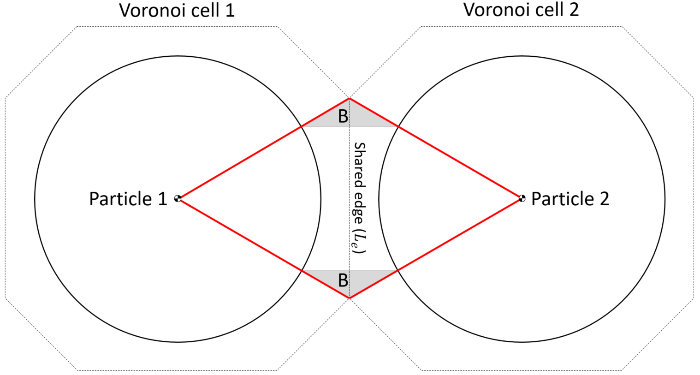
In model A, the following assumptions are made:

For mono-size particles, the rate of heat transfer is given by:

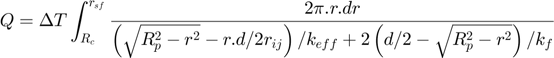
$$Q = \Delta T\int_{R_{c}}^{r_{sf}}\frac{2\pi.r.dr}{\left(\sqrt{R_{p}^{2}-r^{2}}-r.d/2r_{ij}\right)/k_{eff}+2\left(d/2-\sqrt{R_{p}^{2}-r^{2}}\right)/k_{f}}$$

Where:

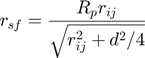
$$r_{sf} = \frac{R_{p}r_{ij}}{\sqrt{r_{ij}^2+d^{2}/4}}$$

For multi-size particles, the rate of heat transfer is given by:

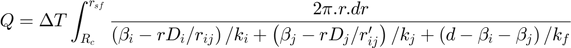
$$Q = \Delta T\int_{R_{c}}^{r_{sf}}\frac{2\pi.r.dr}{\left(\beta_{i}-rD_{i}/r_{ij}\right)/k_{i}+\left(\beta_{j}-rD_{j}/r_{ij}'\right)/k_{j}+\left(d-\beta_{i}-\beta_{j}\right)/k_{f}}$$

Where:

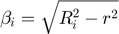
$$\beta_{i} = \sqrt{R_{i}^{2}-r^{2}}$$

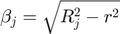
$$\beta_{j} = \sqrt{R_{j}^{2}-r^{2}}$$

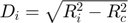$D_{i} = \sqrt{R_{i}^{2}-R_{c}^{2}}$ (if contact)

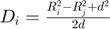$D_{i} = \frac{R_{i}^{2}-R_{j}^{2}+d^{2}}{2d}$ (if non-contact)

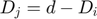
$$D_{j} = d-D_{i}$$

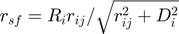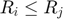$r_{sf} = R_{i}r_{ij}/\sqrt{r_{ij}^{2}+D_{i}^{2}}$ (if $R_{i} \leq R_{j}$)

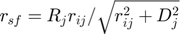$r_{sf} = R_{j}r_{ij}/\sqrt{r_{ij}^{2}+D_{j}^{2}}$ (if $R_{i} > R_{j}$)

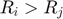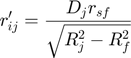
$$r_{ij}' = \frac{D_{j}r_{sf}}{\sqrt{R_{j}^{2}-R_{f}^{2}}}$$

In both cases, the heat transfer radius 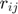$r_{ij}$ depends on the shape and size of the Voronoi cells. There are 3 methods to obtain its value:

The Voronoi diagram is built in a given frequency, and the heat transfer radius is related to the volume V and diameter Le of the double tapered cone as:

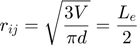
$$r_{ij} = \sqrt{\frac{3V}{\pi d}} = \frac{L_{e}}{2}$$

It has been shown that the average size of the Voronoi cells is related to the porosity of the medium e, in such a way that the heat transfer radius can be computed as:

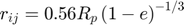
$$r_{ij} = 0.56R_{p}\left(1-e\right)^{-1/3}$$

In this method, instead of building the Voronoi diagram, the local porosity around each particle, considering its immediate neighbors, is computed and updated in a given frequency.

In this method, the value of the average global porosity is directly provided and kept constant, or it is automatically computed by assuming that the total volume of the domain is obtained by the applying the alpha-shape method over all particles.

Notation:

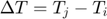$\Delta T = T_{j}-T_{i}$: Temperature difference between elements i and j

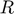$R$: Radius of particles i and j (or p when mono-size)

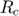$R_{c}$: Contact radius

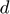$d$: Distance between the center of the particles

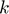$k$: Thermal conductivity of particles i and j, and interstitial fluid f

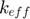$k_{eff}$: Effective contact conductivity

References:

classdef ConductionIndirect_VoronoiA < ConductionIndirect

Public properties

    properties (SetAccess = public, GetAccess = public)
        method  uint8  = uint8.empty;    % flag for type of method to compute voronoi cells size
        coeff   double = double.empty;   % heat transfer coefficient
        tol_abs double = double.empty;   % absolute tolerance for numerical integration
        tol_rel double = double.empty;   % relative tolerance for numerical integration
    end

Constructor method

    methods
        function this = ConductionIndirect_VoronoiA()
            this = this@ConductionIndirect(ConductionIndirect.VORONOI_A);
            this = this.setDefaultProps();
        end
    end

Public methods: implementation of super-class declarations

    methods
        %------------------------------------------------------------------
        function this = setDefaultProps(this)
            this.method  = this.POROSITY_GLOBAL;
            this.tol_abs = 1e-10;
            this.tol_rel = 1e-6;
        end

        %------------------------------------------------------------------
        function this = setFixParams(this,int,drv)
            this.coeff = this.heatTransCoeff(int,drv);
        end

        %------------------------------------------------------------------
        function this = setCteParams(this,~,~)

        end

        %------------------------------------------------------------------
        function this = evalHeatRate(this,int,drv)
            if (isempty(this.coeff))
                h = this.heatTransCoeff(int,drv);
            else
                h = this.coeff;
            end
            this.total_hrate = h * (int.elem2.temperature-int.elem1.temperature);
        end
    end

Public methods: sub-class specifics

    methods
        %------------------------------------------------------------------
        function h = heatTransCoeff(this,int,drv)
            if (int.kinemat.gen_type == int.kinemat.PARTICLE_PARTICLE)
                if (int.elem1.radius == int.elem2.radius)
                    h = this.evalIntegralMonosize(int,drv);
                else
                    h = this.evalIntegralMultisize(int,drv);
                end
            else
                % Assumption: walls are always considered as lines
                h = this.evalIntegralWall(int,drv);
            end
        end

        %------------------------------------------------------------------
        function h = evalIntegralWall(this,int,drv)
            % Needed properties
            Rp = int.elem1.radius;
            Rc = int.kinemat.contact_radius;
            d  = int.kinemat.distc;
            kp = int.elem1.material.conduct;
            kf = drv.fluid.conduct;

            % Parameters
            rij = this.getConductRadius(int,drv,Rp);
            if (rij <= Rc || isinf(rij))
                h = 0;
                return;
            end
            rsf = Rp * rij / sqrt(rij^2 + d^2);

            % Evaluate integral numerically
            fun = @(r) 2*pi*r / ((sqrt(Rp^2-r.^2)-d*r/rij)/kp + (d-sqrt(Rp^2-r.^2))/kf);
            try
                h = integral(fun,Rc,rsf,'ArrayValued',true,'AbsTol',this.tol_abs,'RelTol',this.tol_rel);
            catch
                h = 0;
            end
        end

        %------------------------------------------------------------------
        function h = evalIntegralMonosize(this,int,drv)
            % Needed properties
            Rp = int.elem1.radius;
            Rc = int.kinemat.contact_radius;
            D  = int.kinemat.distc/2;
            ks = int.eff_conduct;
            kf = drv.fluid.conduct;

            % Parameters
            rij = this.getConductRadius(int,drv,Rp);
            if (rij <= Rc || isinf(rij))
                h = 0;
                return;
            end
            rsf = Rp * rij / sqrt(rij^2 + D^2);

            % Evaluate integral numerically
            fun = @(r) 2*pi*r / ((sqrt(Rp^2-r.^2)-D*r/rij)/ks + 2*(D-sqrt(Rp^2-r.^2))/kf);
            try
                h = integral(fun,Rc,rsf,'ArrayValued',true,'AbsTol',this.tol_abs,'RelTol',this.tol_rel);
            catch
                h = 0;
            end
        end

        %------------------------------------------------------------------
        function h = evalIntegralMultisize(this,int,drv)
            % Needed properties
            R1 = int.elem1.radius;
            R2 = int.elem2.radius;
            Rc = int.kinemat.contact_radius;
            d  = int.kinemat.distc;
            k1 = int.elem1.material.conduct;
            k2 = int.elem2.material.conduct;
            kf = drv.fluid.conduct;

            % Parameters
            if (int.kinemat.is_contact)
                D1 = sqrt(R1^2 - Rc^2);
            else
                D1 = (R1^2 - R2^2 + d^2) / (2*d);
            end
            D2 = d - D1;

            ri = this.getConductRadius(int,drv,(R1+R2)/2); % Assumption: average radius
            if (rij <= Rc || isinf(ri))
                h = 0;
                return;
            elseif (R1 <= R2)
                rsf = R1*ri / sqrt(ri^2 + D1^2);
            else
                rsf = R2*ri / sqrt(ri^2 + D2^2);
            end
            rj = D2*rsf / sqrt(R2^2 - rsf^2);

            % Evaluate integral numerically
            fun = @(r) 2*pi*r / ((sqrt(R1^2-r^2)-D1*r/ri)/k1 + (sqrt(R2^2-r^2)-D2*r/rj)/k2 + (d-sqrt(R1^2-r^2)-sqrt(R2^2-r^2))/kf);
            try
                h = integral(fun,Rc,rsf,'ArrayValued',true,'AbsTol',this.tol_abs,'RelTol',this.tol_rel);
            catch
                h = 0;
            end
        end

        %------------------------------------------------------------------
        function r = getConductRadius(this,int,drv,Rp)
            if (this.method == this.VORONOI_DIAGRAM)
                r = int.kinemat.vedge/2;
            else
                if (this.method == this.POROSITY_GLOBAL)
                    por = drv.porosity;
                elseif (this.method == this.POROSITY_LOCAL && int.kinemat.gen_type == int.kinemat.PARTICLE_PARTICLE)
                    por = (int.elem1.porosity+int.elem2.porosity)/2; % Assumption: average porosity
                else
                    por = int.elem1.porosity; % Assumption: particle porosity only
                end
                r = 0.56 * Rp * (1-por)^(-1/3);
            end
        end
    end

end


Published with MATLAB® R2019b