ConductionDirect_Collisional class

Contents

Description

This is a sub-class of the ConductionDirect class for the implementation of the Collisional direct heat conduction model.

This model is based on FEM simulations of the transient heat conduction between colliding spheres assuming elastic collisions according to Hertz theory.

It is suited for dynamic models in which particles are moving and colliding against each other and the contacts last for a very short time.

This collisional contact conduction formula is applied while the current contact time is lower than the expected collision time computed a priori.

When the contact time surpasses the expected collision time, a static contact conduction model is employed. In this case, the Batchelor & O'Brien model is used.

The rate of heat transfer for this collisional model is given by:

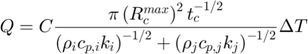
$$Q = C \frac{\pi \left ( R_{c}^{max} \right )^{2} t_{c}^{-1/2}}{\left ( \rho_{i}c_{p,i}k_{i} \right )^{-1/2} + \left ( \rho_{j}c_{p,j}k_{j} \right )^{-1/2}} \Delta T$$

Where:

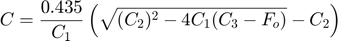
$$C = \frac{0.435}{C_{1}} \left ( \sqrt{(C_{2})^{2} - 4C_{1}(C_{3}-F_{o})} - C_{2} \right )$$

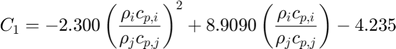
$$C_{1} = -2.300 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right )^{2} + 8.9090 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right ) - 4.235$$

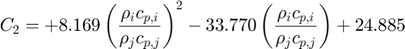
$$C_{2} = +8.169 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right )^{2} - 33.770 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right ) + 24.885$$

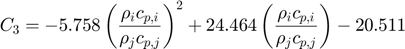
$$C_{3} = -5.758 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right )^{2} + 24.464 \left ( \frac{\rho_{i}c_{p,i}}{\rho_{j}c_{p,j}} \right ) - 20.511$$

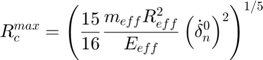
$$R_{c}^{max} = \left ( \frac{15}{16} \frac{m_{eff}R_{eff}^{2}}{E_{eff}} \left ( \dot{\delta}_{n}^{0} \right )^{2} \right )^{1/5}$$

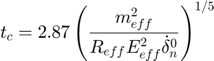
$$t_{c} = 2.87 \left ( \frac{m_{eff}^{2}}{R_{eff}E_{eff}^{2}\dot{\delta}_{n}^{0}} \right )^{1/5}$$

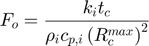
$$F_{o} = \frac{k_{i}t_{c}}{\rho_{i}c_{p,i} \left ( R_{c}^{max} \right )^{2}}$$

Notation:

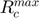$R_{c}^{max}$: Maximum contact radius during collision

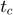$t_{c}$: Collision duration

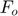$F_{o}$: Fourier number

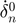$\dot{\delta}_{n}^{0}$: Time rate of change of normal overlap at the impact moment

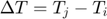$\Delta T = T_{j}-T_{i}$: Temperature difference between elements i and j

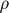$\rho$: Density of elements i and j

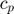$c_{p}$: Heat capacity of elements i and j

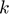$k$: Thermal conductivity of elements i and j

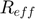$R_{eff}$: Effective contact radius

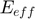$E_{eff}$: Effective Young modulus

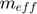$m_{eff}$: Effective mass

References:

classdef ConductionDirect_Collisional < ConductionDirect

Public properties

    properties (SetAccess = public, GetAccess = public)
        coeff    double = double.empty;   % heat transfer coefficient
        col_time double = double.empty;   % expected collision time
    end

Constructor method

    methods
        function this = ConductionDirect_Collisional()
            this = this@ConductionDirect(ConductionDirect.COLLISIONAL);
            this = this.setDefaultProps();
        end
    end

Public methods: implementation of super-class declarations

    methods
        %------------------------------------------------------------------
        function this = setDefaultProps(this)

        end

        %------------------------------------------------------------------
        function this = setFixParams(this,~)
            this.coeff = 0;
            this.col_time = inf;
        end

        %------------------------------------------------------------------
        function this = setCteParams(this,int)
            if (~isempty(this.coeff) && ~isempty(this.col_time))
                return;
            end

            % Individual properties
            rho1 = int.elem1.material.density;
            rho2 = int.elem2.material.density;
            k1   = int.elem1.material.conduct;
            k2   = int.elem2.material.conduct;
            cp1  = int.elem1.material.hcapacity;
            cp2  = int.elem2.material.hcapacity;

            % Interaction properties
            r  = int.eff_radius;
            m  = int.eff_mass;
            y  = int.eff_young;
            v0 = abs(int.kinemat.v0_n);

            % Simplifications
            a1 = rho1 * cp1;
            a2 = rho2 * cp2;
            b  = a1/a2;
            b2 = b^2;

            % Maximum contact radius and total collision time
            Rc = (15 * m * r^2 * v0^2 / (16 * y))^(1/5);
            tc = 2.87 * (m^2 / (r * y^2 * v0))^(1/5);

            % Fourier number
            % Assumption: average for particles
            if (int.kinemat.gen_type == int.kinemat.PARTICLE_PARTICLE)
                F1 = k1 * tc / (rho1 * cp1 * Rc^2);
                F2 = k2 * tc / (rho2 * cp2 * Rc^2);
                F  = (F1 + F2) / 2;
            else
                F = k1 * tc / (rho1 * cp1 * Rc^2);
            end

            % Auxiliary coefficient
            C1 = -2.300*b2 + 8.9090*b - 4.2350;
            C2 =  8.169*b2 - 33.770*b + 24.885;
            C3 = -5.758*b2 + 24.464*b - 20.511;
            C  =  0.435 * (sqrt(C2^2 - 4*C1*(C3-F)) - C2) / C1;

            % Set collision time and heat transfer coefficient
            this.coeff = C * pi * Rc^2 * tc^(-1/2) / ((a1*k1)^(-1/2) + (a2*k2)^(-1/2));
            this.col_time = tc;
        end

        %------------------------------------------------------------------
        function this = evalHeatRate(this,int)
            % Compute heat rate according to current contact time
            if (int.kinemat.contact_time < this.col_time)
                % Collisional conduction: Collisional formula
                this.total_hrate = this.coeff * (int.elem2.temperature-int.elem1.temperature);
            else
                % Static conduction: Batchelor & O'Brien formula
                this.total_hrate = 4 * int.eff_conduct * int.kinemat.contact_radius * (int.elem2.temperature-int.elem1.temperature);
            end
        end
    end

end


Published with MATLAB® R2019b