AreaCorrect_LMLB class

Contents

Description

This is a sub-class of the AreaCorrect class for the implementation of the Lu, Morris, Li, Benyahia contact area correction model.

This model computes the reduced radius of the contact area by applying a correction coefficient derived for the linear spring-dashpot model:

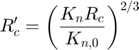
$$R_{c}' = \left(\frac{K_{n}R_{c}}{K_{n,0}}\right)^{2/3}$$

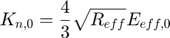
$$K_{n,0} = \frac{4}{3}\sqrt{R_{eff}}E_{eff,0}$$

Where:

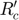$R_{c}'$: Reduced radius of contact area

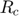$R_{c}$: Contact area radius originally computed in the simulation

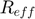$R_{eff}$: Effective contact radius

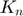$K_{n}$: Normal stiffness coefficient used in the simulation

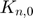$K_{n,0}$: Normal stiffness coefficient derived from the real value of the Young modulus

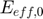$E_{eff,0}$: Effective Young modulus with the real value

References:

classdef AreaCorrect_LMLB < AreaCorrect

Constructor method

    methods
        function this = AreaCorrect_LMLB()
            this = this@AreaCorrect(AreaCorrect.LMLB);
        end
    end

Public methods: implementation of super-class declarations

    methods
        %------------------------------------------------------------------
        function this = fixRadius(this,int)
            if (~isempty(int.cforcen))
                kn = int.cforcen.stiff;
            else
                % Assumption: computed as kn0 but with modified Young modulus
                kn = 4 * sqrt(int.eff_radius) * int.eff_young / 3;
            end
            kn0 = 4 * sqrt(int.eff_radius) * int.eff_young0 / 3;
            int.kinemat.contact_radius = (kn*int.kinemat.contact_radius/kn0)^(2/3);
        end
    end

end


Published with MATLAB® R2019b