The Stokes equations¶
\begin{align*}
-\Delta \mathbf{u} + \nabla p &= \mathbf{f} &&\text{in } \Omega,\\
\nabla \cdot \mathbf{u} &= 0 &&\text{in } \Omega,\\
\mathbf{u} &= \mathbf{0}&&\text{on } \partial\Omega.
\end{align*}
In this tutorial you will learn how to:
- Create manufactured solutions with UFL
- Use block-preconditioners
Defining a manufactured solution¶
In [4]:
def u_ex(x):
sinx = sin(pi * x[0])
siny = sin(pi * x[1])
cosx = cos(pi * x[0])
cosy = cos(pi * x[1])
c_factor = 2 * pi * sinx * siny
return c_factor * as_vector((cosy * sinx, - cosx * siny))
def p_ex(x):
return sin(2 * pi * x[0]) * sin(2 * pi * x[1])
In [5]:
def source(x):
u, p = u_ex(x), p_ex(x)
return - div(grad(u)) + grad(p)
Defining the variational form¶
$$\begin{align}
A w &= b,\\
\begin{pmatrix}
A_{\mathbf{u},\mathbf{u}} & A_{\mathbf{u},p} \\
A_{p,\mathbf{u}} & 0
\end{pmatrix}
\begin{pmatrix} u\\ p \end{pmatrix}
&= \begin{pmatrix}\mathbf{f}\\ 0 \end{pmatrix}
\end{align}$$
In [6]:
def create_bilinear_form(V, Q):
u, p = TrialFunction(V), TrialFunction(Q)
v, q = TestFunction(V), TestFunction(Q)
a_uu = inner(grad(u), grad(v)) * dx
a_up = inner(p, div(v)) * dx
a_pu = inner(div(u), q) * dx
return fem.form([[a_uu, a_up], [a_pu, None]])
In [7]:
def create_linear_form(V, Q):
v, q = TestFunction(V), TestFunction(Q)
domain = V.mesh
x = SpatialCoordinate(domain)
f = source(x)
return fem.form([inner(f, v) * dx,
inner(fem.Constant(domain, 0.), q) * dx])
Create a block preconditioner¶
In [10]:
def create_preconditioner(Q, a, bcs):
p, q = TrialFunction(Q), TestFunction(Q)
a_p11 = fem.form(inner(p, q) * dx)
a_p = fem.form([[a[0][0], None],
[None, a_p11]])
P = fem.petsc.assemble_matrix_nest(a_p, bcs)
P.assemble()
return P
Assemble the nested system¶
In [11]:
def assemble_system(lhs_form, rhs_form, bcs):
A = fem.petsc.assemble_matrix_nest(lhs_form, bcs=bcs)
A.assemble()
b = fem.petsc.assemble_vector_nest(rhs_form)
fem.petsc.apply_lifting_nest(b, lhs_form, bcs=bcs)
for b_sub in b.getNestSubVecs():
b_sub.ghostUpdate(addv=PETSc.InsertMode.ADD,
mode=PETSc.ScatterMode.REVERSE)
spaces = fem.extract_function_spaces(rhs_form)
bcs0 = fem.bcs_by_block(spaces, bcs)
fem.petsc.set_bc_nest(b, bcs0)
return A, b
PETSc Krylov Subspace solver¶
In [12]:
def create_block_solver(A, b, P, comm):
ksp = PETSc.KSP().create(comm)
ksp.setOperators(A, P)
ksp.setType("minres")
ksp.setTolerances(rtol=1e-9)
ksp.getPC().setType("fieldsplit")
ksp.getPC().setFieldSplitType(PETSc.PC.CompositeType.ADDITIVE)
nested_IS = P.getNestISs()
ksp.getPC().setFieldSplitIS(("u", nested_IS[0][0]),
("p", nested_IS[0][1]))
# Set the preconditioners for each block
ksp_u, ksp_p = ksp.getPC().getFieldSplitSubKSP()
ksp_u.setType("preonly")
ksp_u.getPC().setType("gamg")
ksp_p.setType("preonly")
ksp_p.getPC().setType("jacobi")
# Monitor the convergence of the KSP
ksp.setFromOptions()
return ksp
Solving the Stokes problem with a block-preconditioner¶
In [14]:
def solve_stokes(u_element, p_element, domain):
V = fem.FunctionSpace(domain, u_element)
Q = fem.FunctionSpace(domain, p_element)
lhs_form = create_bilinear_form(V, Q)
rhs_form = create_linear_form(V, Q)
bcs = create_velocity_bc(V)
nsp = create_nullspace(rhs_form)
A, b = assemble_system(lhs_form, rhs_form, bcs)
assert nsp.test(A)
A.setNullSpace(nsp)
P = create_preconditioner(Q, lhs_form, bcs)
ksp = create_block_solver(A, b, P, domain.comm)
u, p = fem.Function(V), fem.Function(Q)
w = PETSc.Vec().createNest([u.vector, p.vector])
ksp.solve(b, w)
assert ksp.getConvergedReason() > 0
u.x.scatter_forward()
p.x.scatter_forward()
return compute_errors(u, p)
Crouzeix-Raviart¶
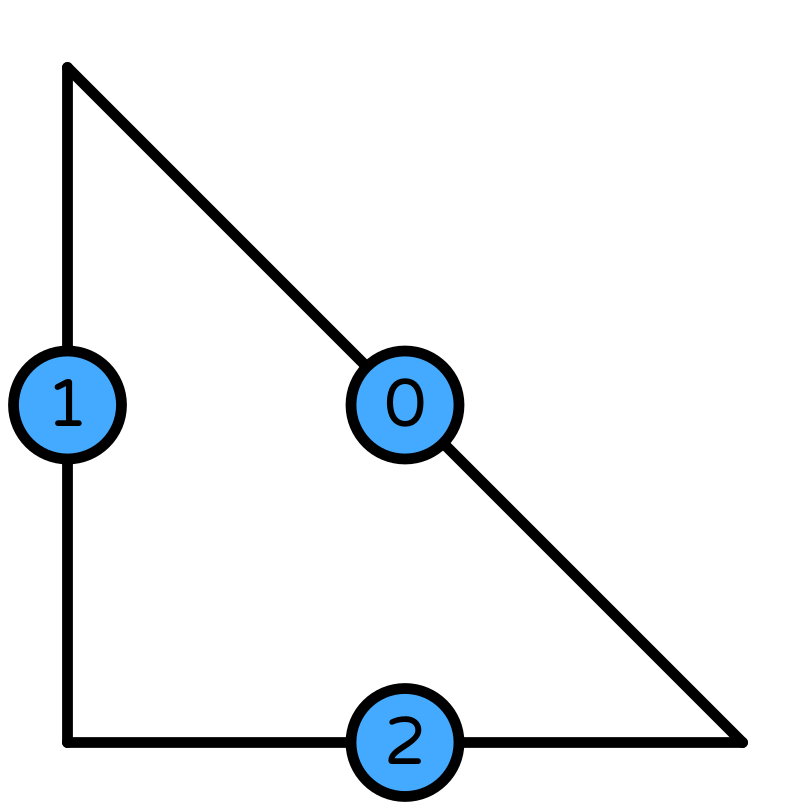

In [18]:
element_u = VectorElement("CR", "triangle", 1)
element_p = FiniteElement("DG", "triangle", 0)
error_plot(element_u, element_p, 1)
Piecewise linear pressure space¶

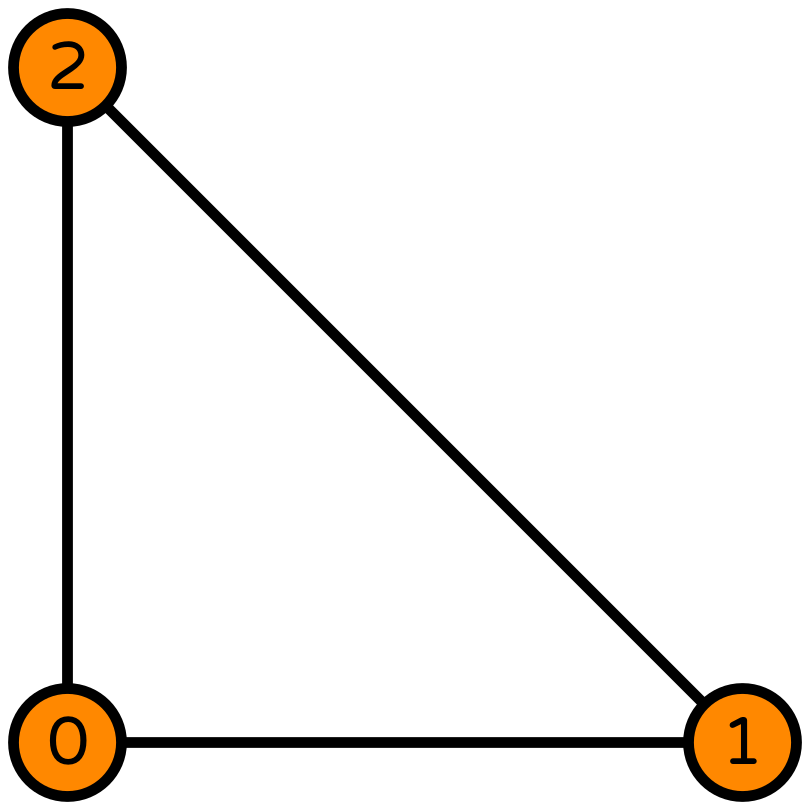
In [19]:
enriched_element = (
FiniteElement("Lagrange", "triangle", 2)
+ FiniteElement("Bubble", "triangle", 3))
element_u = VectorElement(enriched_element)
element_p = FiniteElement("DG", "triangle", 1)
error_plot(element_u, element_p, 2)
Taylor-Hood Element¶

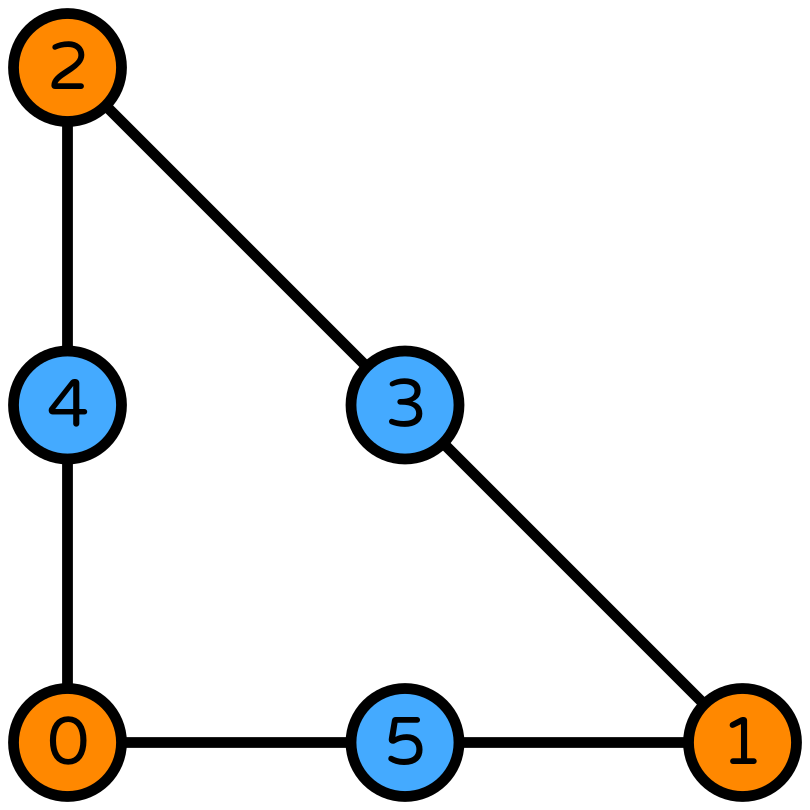
In [24]:
element_u = VectorElement("CG", "triangle", 3)
element_p = FiniteElement("CG", "triangle", 2)
error_plot(element_u, element_p, 3)