Slides.knit

class: center, inverse, middle

.pull-left-wide {
  float: left;
  width: 66%;
}
.pull-right-wide {
  float: right;
  width: 66%;
}
.pull-right-wide ~ p {
  clear: both;
}

.pull-left-narrow {
  float: left;
  width: 30%;
}
.pull-right-narrow {
  float: right;
  width: 30%;
}

.pull-right-extra-narrow {
  float: right;
  width: 20%;
}

.pull-center {
  margin-left: 28%;
  width: 44%;
}

.pull-center-wide {
  margin-left: 17%;
  width: 66%;
}

.pull-center-medium {
  margin-left: 20%;
  width: 60%;
}

.tiny123 {
  font-size: 0.40em;
}

.small123 {
  font-size: 0.80em;
}

.large123 {
  font-size: 2em;
}

.red {
  color: red
}

.chaosred {
  color: #b33d3d
}

.orange {
  color: orange
}

.green {
  color: green
}

.blue {
  color: blue
}
</style>

# CHAOS
## Converting Historical Accounts to Occupational Scores

### Matt Curtis, Torben Johansen, Julius Koschnick, **Christian Vedel**,
### University of Southern Denmark

### Email: [christian-vs@sam.sdu.dk](christian-vs@sam.sdu.dk)

### Updated 2025-10-09

---

.pull-left[
# The problem

- Archives are **rich in occupations**, but **sparse in individual incomes**.
- Standard workaround: impute income with **occupational scores** (e.g., IPUMS **OCCSCORE**).
- But fixed benchmarks (e.g., 1950 US wages) can **misstate levels and trends** across **time, place, and titles**.

]

.pull-right[
### Use of OCCSCORE (examples)
.small123[
- Abramitzky, Boustan & Eriksson (2014): Assimilation of immigrants 1900–1920 using what a median US worker earned in 1950 (OCCSCORE adjusted back).  
- Ager, Boustan & Eriksson (2021): Recovery of Southern slaveholder families after the Civil War, comparing wealth shocks, with adjustments based on occupation-based earnings proxies from later censuses.
Abramitzky, Ager, Boustan, Cohen & Hansen, C. W. (2023): Migration does not offset local wages (as proxied by their occupation and a few other characteristics)
- Collins & Wanamaker (2014): Uses occupational scores to measure the effects, on income, from the great internal migration among africian americans in the period 1910-1930s

*Amazing paper in the age before high-powered machine learning*
- But now we can do better
]

]

---
<br>
<br>
<br>
<br>

# Three problems:

1. **Source-Target drift:** Problematic to estimate effects in e.g. 1900 based on 1950s wages
2. **Within Occupation variation:** All bakers do not earn the same
3. **Hard to construct:** Constructing new measures is time consuming.

.footnote[
.chaosred[*1. and 2. causes systematic bias* (Saavedra, Twinam, 2020; Inwood, Minns and Summerfield, 2019)] 
]

--
#### .chaosred[*We address all of these to some extend*]

---

.pull-left[
# CHAOS
- This paper introduces a method for:  
  + **C**onverting (using maths)
  + **H**istorical **A**ccounts (e.g. wage tables)
  + **O**ccupational **S**cores (something like IPUMS occscore [but better])

### Some points:
- .chaosred[**Still preliminary**]
- Different than Saavedra & Twinam (2020) `$\leftrightarrow$` Not a classical supervised ML approach
- Different than Paker, Stephenson, Wallis (2025) `$\leftrightarrow$` Produces estimates across occupations
- Fully automatic and highly interpretable + comes with built in debiasing (even more preliminary)

]

.pull-right[
### Four introductions
.panelset[
.panel[.panel-name[1 Straight forward]
- If I give you this:
.pull-right-wide[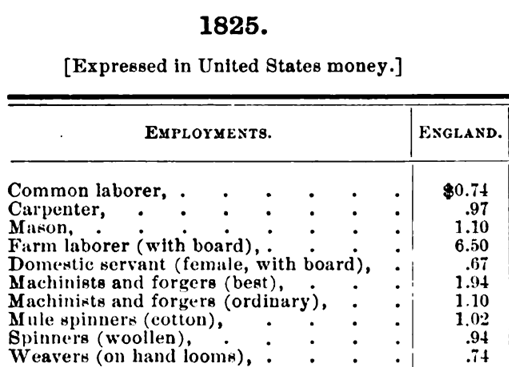
![wages](Figures/Wages1825.png)
]

.pull-left-wide[
- Could you then tell me the approximate income of:
  + Joiner,
  + Cowherd,
  + Bricklayer?
  
- **CHAOS** tells you the appropriate weighted mean

]

.panel[.panel-name[2 Technical]
Given classifier (of `$h_j$`):
$$
d_i \mapsto Pr(h_j\mid d_i)
$$
And a source 
$$
d_i \mapsto y_i \qquad\text{e.g. income}
$$

Can we combine them into a function, `$f$`, to estimate new outcomes:

$$
f:\qquad d_k\mapsto\mathbb{E}(y_k \mid d_k)
$$

]

.panel[.panel-name[3 Casual]
> "Yo! I've got this table of people's income from 1825. Do you think we could somehow sort of apply it to incomes for occupations across this census data?"

![CHAOS](Figures/CHAOS_clipart.png)

]

.panel[.panel-name[4 Collegial]
*We are trying to replace IPUMS occscore*
]

]

---
<br>
<br>
<br>
<br>
<br>
# A disclaimer

--
.pull-right[
.pull-left-narrow[![Warning](Figures/warning.svg)]

.pull-right-wide[
This is not:
 - A magic bullet
 - An excuse to not care about source criticism
 - (In fact a key econometric result is the *'relevance assumption'*)
]

]

---
# Sneakpeak: Where we are getting to
*Given a source:*
.pull-center-medium[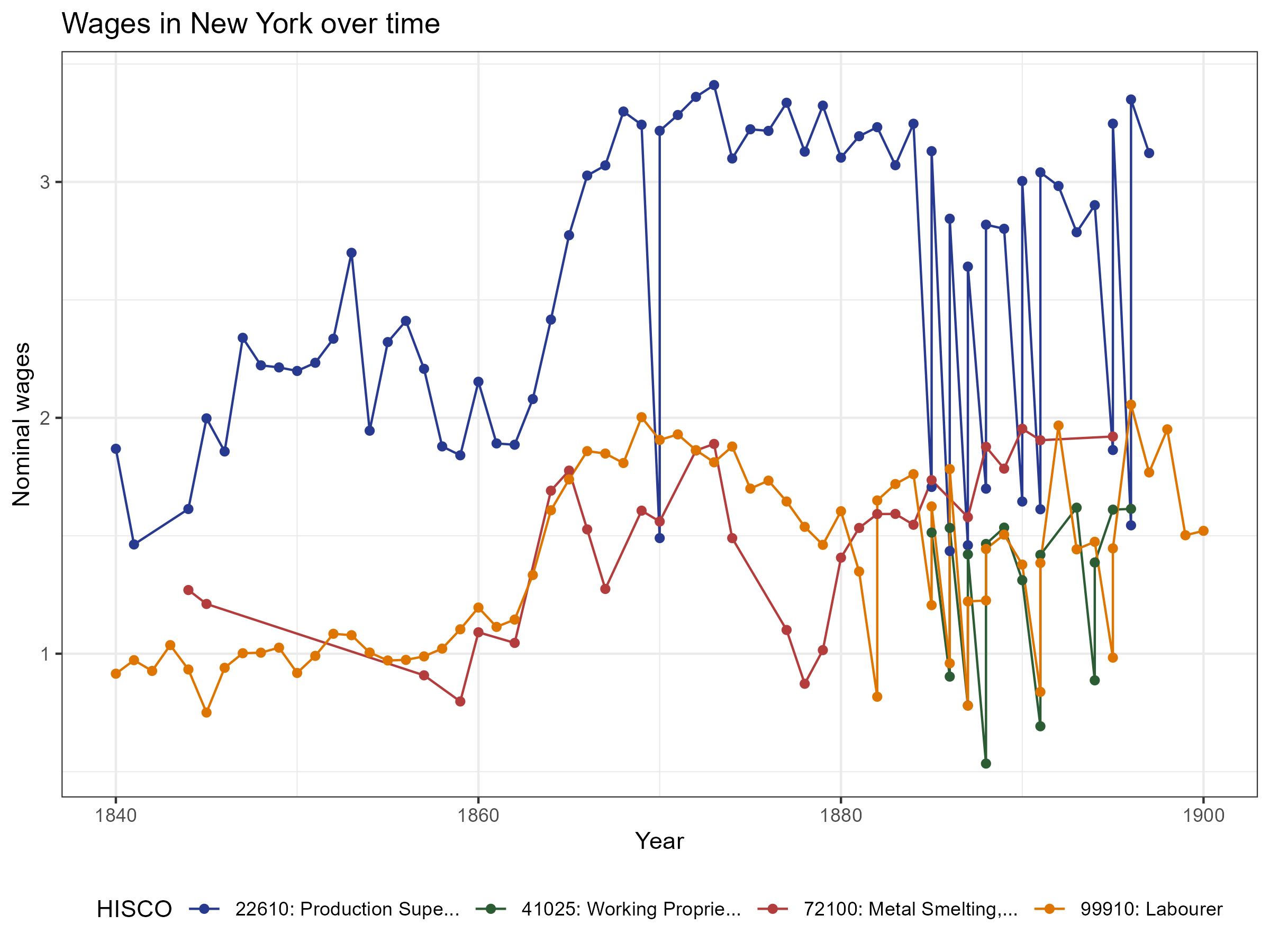
![NY example](Figures/wages_ny_over_time.png)

]

---
class: middle

# Mostly harmless maths

.pull-left[
.small123[
#### Target / Source

We are interested in
`$$\mathbb{E}(y_k \mid d_k).$$`
(The expected income of observation, `$k$`, given occupational description `$d_k$`)

What we have is observations containing

`$$\mathbb{E}(y_i \mid d_i).$$`
(The expected income of observation, `$i$`, given occupational description `$d_i$`)

#### Assumption:
1. **Source-Target relevance:** Good historian's assumption: Your Source must be relevant for your target: `$i$` and `$k$` are both iid draws from the same distribution
2. **Broadband** You have a *broadband* way of classifying occupational descriptions which captures the mean: `$\mathbb{E}(y_i \mid h_j, d_i) = \mathbb{E}(y_i \mid h_j)$` 
]
]

.pull-right[
.small123[

]

#### What you then get:
`$$\mathbb{E}(y_i\mid d_i) = \mathbb{E}(y_k\mid d_k)$$`
So the task is just to get a function which can estimate `$$\mathbb{E}(y_i\mid d_i)$$`

Our approach:
1. Calculate HISCO-level averages: `$$\mathbb{E}(y_i \mid h_j)$$`
2. Estimate how well target descriptions fit HISCO codes

Secret sauce: We can estimate: `$$\Pr(h_j\mid d_i)$$`

]

---
class: middle
# OccCANINE

.pull-left[
.small123[
w. Christian Møller Dahl & Torben Johansen   
https://arxiv.org/abs/2408.00885
]

- We train a language model on ~18.5 million observations spanning 13 different language from 29 different sources
- Open source, user friendly, fast and highly accurate

- **Importantly:** Gives us a probability of each HISCO code given a textual description.

$$
\text{OccCANINE}: \qquad d_i \mapsto Pr(h_j\mid d_i)
$$

- Using basic tricks of probability we can tease out an estimator from this!

]

.pull-right[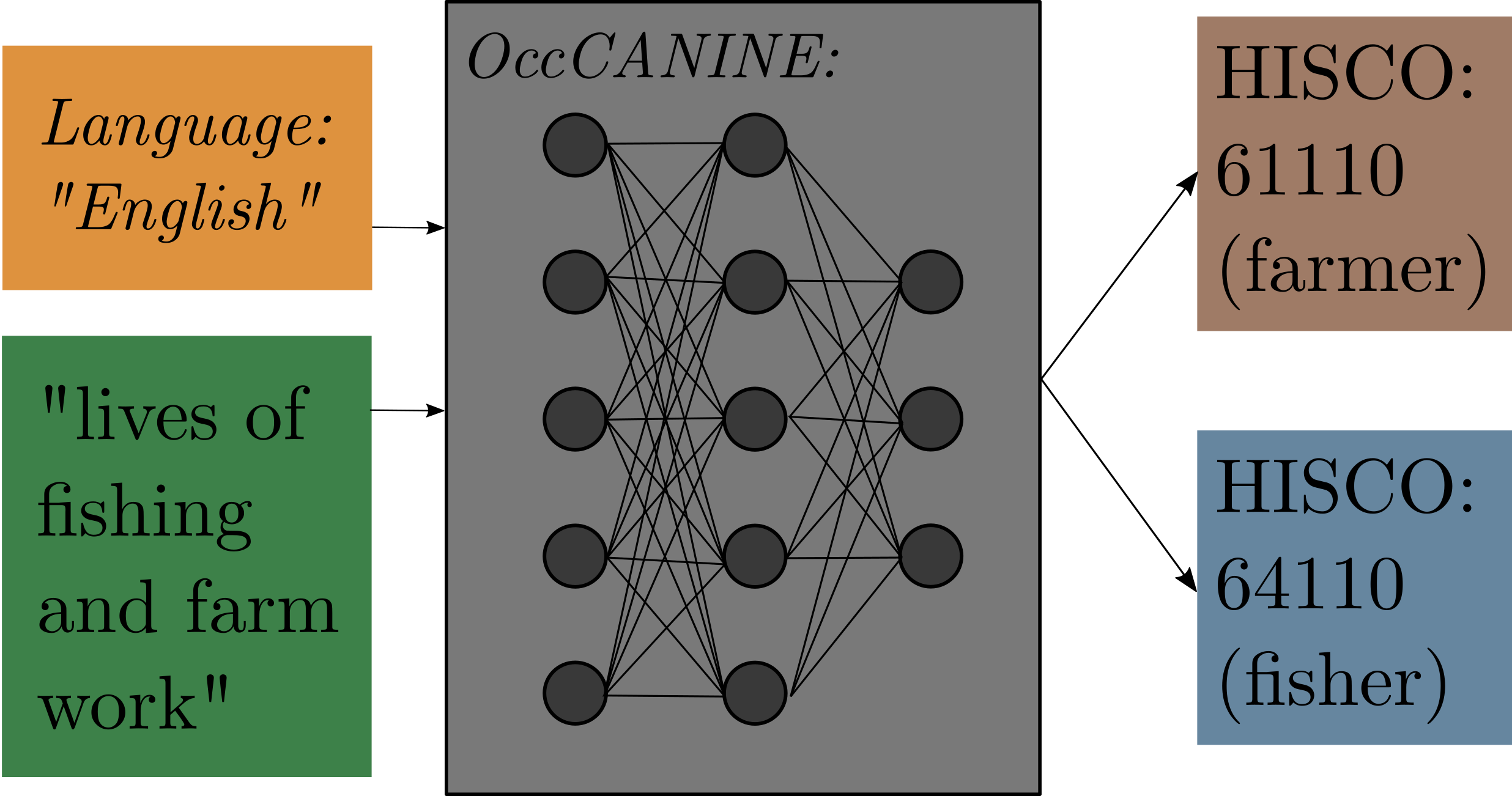
![Archirecture](Figures/Architecture_small.png) 
*Figure 1: Conceptual architecture*

.small123[
#### Outputs a probability of belonging to standardized occupational codes
]

]

---
## More mostly harmless maths

.pull-left[

### .chaosred[Source to HISCO]

`$$\mathbb{E}(y_i\mid h_j)\;=\; \sum_{i\in \mathcal{S}} y_iw_{ij} \;=\; \sum_{i \in \mathcal{S}} y_i \;\frac{\overset{OccCANINE}{\overbrace{Pr(h_j\mid d_i)}}\;\overset{Prior}{\overbrace{Pr(d_i)}}}{\underset{Evidence}{\underbrace{Pr(h_j)}}}$$`

#### Example
We estimate that HISCO 83110 "Blacksmith" earns $2.52 a day since this is the sum:
`$$2.49\times 0.8878 + 3.96\times 0.0568 + ...$$`

]

.pull-right[
### .chaosred[HISCO to Target]
`$$\mathbb{E}(y_k\mid d_k) \;=\;  \sum_{j\in \mathcal{H}} \hat{y}_j w_{jk} \;=\; \sum_{j \in \mathcal{H}} {\underset{\text{from above}}{\underbrace{\mathbb{E}(y_i\mid h_j)}}}  \overset{OccCANINE}{\overbrace{Pr(h_j\mid  d_k)}}$$`

#### Example:
`"mainly blacksmith (also farmer)"` gets a wage `$\hat{y}_k$` assigned from both the HISCO codes for blacksmith (0.95) but also farmer (0.02) etc.

]

.footnote[
.small123[
`$i$`: Index of source; `$j$`: Index in HISCO table; `$k$`: Index of target table
]
]

---
# Demonstration
[Notebook]

---
# Not so harmless maths

.pull-left[
.small123[
### More than one source?
$$
\mathbb{E}(y_i\mid h_j)=\sum_i \left[ y_i \sum_s \left( 
    \frac{\overset{OccCANINE}{\overbrace{Pr(h_j\mid y_i, S_s)}}\overset{Prior}{\overbrace{Pr(y_i\mid S_s)}} \overset{\textit{Source weight}}{\overbrace{Pr(S_s)}}}{\underset{Normalization}{\underbrace{Pr(h_j)}}} \right) \right]
$$

### What if we input gibberish?
Then we get:
$$
`\begin{split}
Classifier:\qquad &Pr(h_j\mid d_k) \;=\; Pr(h_j), \qquad \text{(bd cond. prob.)} \\
CHAOS:\qquad &\mathbb{E}(y_k|d_k) \;= \mathbb{E}(y_i)
\end{split}`
$$
I.e. we just get the mean from the source
]
]

.pull-right[

#### Debiasing & scaling
.small123[
- Bias and scaling problems `$\mathbb{E}(\hat{y}_k)\neq\mathbb{E}(y_k)$` and `$\mathbb{V}(\hat{y}_k)\neq\mathbb{V}(y_k)$`  
- But we can observe this problem if we are willing to assume:
$$
`\begin{split}
\mathbb{E}( y_k-\hat{y}_k) = \mathbb{E}(y_i-\hat{y}_i) \\
\mathbb{V}( y_k-\hat{y}_k) = \mathbb{V}(y_i-\hat{y}_i)
\end{split}`
$$
True under *relevance assumption*  
`$\rightarrow$` Means that we can use PPI and DSL (Angelopoulos et al, 2023; Egami et al 2024)
]

]

---
class: middle

# PPI style bias correction example

.pull-left-wide[
- Say we are interested in the mean of income: `$\mu(y)$`
- But we only observe `$\hat{y}$`
- And we have a small validation set, `$k$`, where we observe both `$y$` and `$\hat{y}$`.
- `$\hat{y}$` might be biased: `$\mu(y)\not\approx \mu(\hat{y})$`
- **Solution:**
`$$\mu(y)\approx \mu(\hat{y})+\frac{1}{k}\mu(y-\hat{y})$$`
]

.footnote[
.chaosred[*There are versions of this that generalises into regression*]
]

---
<br>
<br>
<br>

# Bias correction via self-validation

.pull-left-wide[
- If you trust you own source, you can use LOO-CV self-validation to debias
  1. Leave out `$i^*$` in source
  2. Estimate prediction from `$i^*$` for each source observation
  3. Use CHAOS on the predicted errors to obtain `$\widehat{B}(d)$`
  4. Repeat for all observations to recover error estimate for all source observations
  
- Under Source-Target relevance, we can now estimate bias for new observations `$B(d_k)$` using CHAOS.
  
*LOO can be implemented very quickly (and exactly) via weights updating*

.chaosred[**Code still needs to be implemented**]
]

.pull-right-narrow[
> Whenever you run a regression you can correct for the bias via `$$\hat\beta \;=\; \hat\beta_{\text{naive}} + (X'X)^{-1}X'\widehat{B}(d)$$`

> `$\rightarrow$` Unbiased results

]

---
# Application: Setup

.pull-left-wide[
#### 1. We apply this to a table of wages for 84000 occupations (US Commissioner of Labor)
  + Across 140 places (states and countries) 
  + In the period 1725-1900
  
#### 2. We combine this with measure for skills (routine, mechanical, cognitive) obtained from the *London's Trademan* (1747)
  + Using embedding distance
  + Please ask about details
  
#### 3. We turn everything into a HISCO-level panel using .chaosred[**CHAOS**]
  + **Result:** Occupation level panel of incomes and skills

]

.pull-right-narrow[
.panelset[
.panel[.panel-name[Wages 1]
![COL frontpage](Figures/col-cover.png)

]
.panel[.panel-name[Wages 2]
![COL table](Figures/col-first-tab.png)

]

.panel[.panel-name[Skills]
![LTM frontpage](Figures/ltm.png)

]

.panel[.panel-name[Skills]
![LTM frontpage](Figures/ltm_example.png)

]

---
# Application: Result

.pull-left-narrow[
### What is good advice in 1800?
- Which 18th skills would benefit in the 19th century?

- VERY preliminary
]

.pull-right-wide[
![Result](Figures/skill_premia_over_time_usa.png)
]

---
# Conclusion

.pull-left[
- Here's a new tool (on its way)
- We hope its useful

- More work to be done on:
  + Automatic debiasing
  + Application
  
  
#### Feel free to contact me
**Email:** <christian-vs@sam.sdu.dk>;  
**Twitter/X:** [@ChristianVedel](https://twitter.com/ChristianVedel);  
**BlueSky:** [@christianvedel.bsky.social](https://bsky.app/profile/christianvedel.bsky.social);
]

.pull-right[
.pull-left-wide[
### The entire pipeline of CHAOS
![Archirecture](Figures/CHAOS.png) 
]
]

---
class: middle, center

# Appendix

---
# How it works

.pull-right-wide[
.panelset[
.panel[.panel-name[Steps 1]
.pull-right-wide[
![blacksmith](Figures/blacksmith_example.svg)
]
]
.panel[.panel-name[Step 2]
.pull-right-wide[
![blacksmith and farmer](Figures/blacksmith_and_farmer_example.svg)
]
]
]

]

---
class: middle

# Skills from LTM

.pull-left-wide[
### Extracting skills
- We ask `gpt-4o` to return a JSON of each occupations skills

### Measuring skills
- First, we map the list skills in an occupation, `$S = \{s_1, \dots, s_N\}$`, into a 384-dimensional vector space  using a a pre-trained Sentence-BERT model (all-MiniLM-L6-v2). This yields embedding vectors `$\mathbf{e}_{s_i} \in \mathbb{R}^d$`.

- We then construct a index of skill based on cosine similarity

`$$\text{routine proportion}_i = \frac{\bar{\sigma}_{i,\text{routine}}}{\bar{\sigma}_{i,\text{routine}} + \bar{\sigma}_{i,\text{non routine}}}$$`

Where `$\bar{\sigma}_{i,routine}$` is the cosine similarity between skills$_i$ and the description of `$\text{routine}$`.

]

.pull-right-narrow[
.panelset[
.panel[.panel-name[Goldsmith skills]
.tiny123[
`"making all manner of utensils in gold or silver for ornament or use"`,  
`"performing work in the mould or beating into figure by hammer or other engine"`,  
`"casting works with raised figures in moulds"`,  
`"polishing and finishing cast works"`,  
`"beating plates or dishes of silver from thin flat plates"`,  
`"forming tankards and other vessels from thin plates soldered together"`,  
`"beating mouldings for vessels"`,  
`"using flatting-mills to reduce metal to required thinness"`,  
`"making all moulds for their work"`  
]
]

.panel[.panel-name[Routine]
.small123[
#### Routine
repetitive task, following explicit rules, highly structured sequence

#### Non-routine
problem solving, creative thinking, requires judgment
]
]

.panel[.panel-name[Cognitive]
.small123[
#### Cognitive
abstract reasoning, analytical thinking, information processing

#### Non-cognitive
physical effort, manual labor, emotional labor
]
]

.panel[.panel-name[Cognitive]
.small123[
#### Mechanical
operate machinery, assemble parts, machine operation

#### Non-mechanical
software use, writing, communication
]
]

]

---
class: middle
# Appendix Example: New York, 1880

### "He is a blacksmith"

We want to estimate an income for a census record  
with only an occupational title.

We start from a **source table** of daily wages in New York, 1880:

.small123[
| Source title `$d_i$`  | Outcome `$y_i$` (daily wage) |
|---------------------|----------------------------|
| Blacksmith          | $2.80 |
| Hammersmith         | $2.55 |
| Tinsmith            | $2.30 |
| Goldsmith           | $3.10 |
| Shoemaker           | $2.40 |
| (other)             | ...   |
]
---

# Step A1: Classifier probabilities

OccCANINE assigns each source title `$d_i$` a distribution over HISCO codes:

`$$\Pr(h_j \mid d_i)$$`

.small123[
| `$d_i$`       | `$Pr(83110\mid d_i)$` | `$Pr(83120\mid d_i)$` | `$Pr(87340\mid d_i)$` | `$Pr(88050\mid d_i)$` | `$Pr(80110\mid d_i)$` |
|-------------|----------------------|-----------------------|--------------------|---------------------|---------------------|
| Blacksmith  | 0.955 | 0.011 | 0.018 | 0.013 | 0.003 |
| Hammersmith | 0.112 | 0.851 | 0.031 | 0.000 | 0.006 |
| Tinsmith    | 0.069 | 0.000 | 0.911 | 0.018 | 0.002 |
| Goldsmith   | 0.074 | 0.011 | 0.012 | 0.901 | 0.002 |
| Shoemaker   | 0.011 | 0.000 | 0.012 | 0.000 | 0.977 |
]

- 83110: Blacksmith
- 83120: Hammersmith
- 87340: Tinsmith
- 88050: Goldsmith
- 80110: Shoemaker

---

# Step A2: Posterior probabilities

Via Bayes rule, we invert to `$\Pr(d_i \mid h_j)$`:

.small123[
| `$d_i$`       | `$Pr(d_i\mid 83110)$` | `$Pr(d_i \mid 83120)$` | `$Pr(d_i \mid 87340)$` | `$Pr(d_i \mid 88050)$` | `$Pr(d_i \mid 80110)$` |
|-------------|------------|-------------|----------|-----------|-----------|
| Blacksmith  | 0.782 | 0.013 | 0.018 | 0.014 | 0.003 |
| Hammersmith | 0.092 | 0.975 | 0.032 | 0.000 | 0.006 |
| Tinsmith    | 0.057 | 0.000 | 0.926 | 0.019 | 0.002 |
| Goldsmith   | 0.061 | 0.013 | 0.012 | 0.967 | 0.002 |
| Shoemaker   | 0.009 | 0.000 | 0.012 | 0.000 | 0.987 |
]

- 83110: Blacksmith
- 83120: Hammersmith
- 87340: Tinsmith
- 88050: Goldsmith
- 80110: Shoemaker

---

# Step A3: HISCO-level means

Aggregate outcomes into HISCO-level expected values:

`$\; y_j = \sum_i y_i \Pr(d_i \mid h_j)$`

.small123[
| HISCO code | Occupation          | `$\mathbb{E}(y_i\mid h_j)$` |
|------------|--------------------|---------------------------|
| 83110      | Blacksmith         | 2.76 |
| 83120      | Hammersmith        | 2.56 |
| 87340      | Tinsmith           | 2.33 |
| 88050      | Goldsmith          | 3.08 |
| 80110      | Shoemaker          | 2.40 |
]

---

# Step B1: Target classification

Target record: *“He is a blacksmith”*

OccCANINE distribution over HISCO:

.small123[
| Target `$d_k$` | Blacksmith | Hammersmith | Tinsmith | Goldsmith | Shoemaker |
|--------------|------------|-------------|----------|-----------|-----------|
| "He is a blacksmith" | 0.918 | 0.019 | 0.032 | 0.016 | 0.015 |
]

---

# Step B2: Target prediction

Estimate `$\hat y_k = \sum_j y_j \Pr(h_j\mid d_k)$`

`$$\hat y_k = 2.76\cdot0.918 + 2.56\cdot0.019 + 2.33\cdot0.032 + 3.08\cdot0.016 + 2.40\cdot0.015$$`

$$\hat y_k \;\approx\; \$2.75$$

**Prediction:** A census record with “blacksmith” in 1880 New York  
gets an estimated daily wage of $2.75.

---

# Step C: Collapsed weights

We can collapse HISCO and express weights `$w_{ik}$` directly:

.small123[
| Source `$d_i$` | Weight `$w_{ik}$` |
|--------------|-----------------|
| Blacksmith   | 0.719 |
| Hammersmith  | 0.104 |
| Tinsmith     | 0.082 |
| Goldsmith    | 0.072 |
| Shoemaker    | 0.023 |
]

So prediction = weighted average:

`$$\hat y_k = 0.719\cdot2.80 + 0.104\cdot2.55 + 0.082\cdot2.30 + 0.072\cdot3.10 + 0.023\cdot2.40$$`

= **$2.75**

---

class: middle
# Interpretation

- Majority weight: **Blacksmith** row (0.719)  
- Related trades contribute: Hammersmith, Tinsmith, Goldsmith  
- Even Shoemaker leaves a small trace  
- **Not a black box:** full transparency on how the estimate is built

---
class: middle
# Example 1

.pull-left-wide[
- Suppose the source reports an income of $3.10 for "smiths." 
- In HISCO, there are several possibilities: blacksmith, tinsmith, and goldsmith. Instead of forcing a hard choice, CHAOS distributes the weight across codes. 
- If historical usage suggests "smith" usually means blacksmith, we might assign `$w_{ij}=0.7$` to blacksmith, `$w_{ij}=0.2$` to tinsmith, and `$w_{ij}=0.1$` to goldsmith. 
- The CHAOS equations thereby preserve the ambiguity and propagate it through to the estimates. 
]

---
class: middle
# Example 2

.pull-left-wide[
- Sometimes a historical record lists multiple occupations for the same person
- For instance, "farmer and butcher'" with an average income of $2.50. In HISCO, these map to two codes.
- Instead of forcing a choice, CHAOS splits the weights, say `$w_{ij}=0.7$` for farmer and `$w_{ij}=0.3$` for butcher.  
]