Bayesian hypothesis testing
PSM 2
Bennett Kleinberg
5 March 2019
Probability, Statistics & Modeling II
Today
Bayesian statistics
- What is it? & How does it differ from NHST?
- What can it solve?
- Why should I care?
- How do I do it?
What is Bayesian Statistics?
What is it?
Rewind:
Null hypothesis significance testing
Hypothesis testing the old way
Hypothesis testing the old way
Hypothesis testing the old way
NULL hypothesis testing
- \(H_0\) : \(M_A \approx M_B\)
- there is no difference in the means between Group A and Group B
- \(H_A\) : \(M_A \neq M_B\)
- there is a difference in the means between Group A and Group B
Directed hypotheses:
- \(H_A\) : \(M_A > M_B\)
- \(H_A\) : \(M_A < M_B\)
Hypothesis testing the old way
NULL hypothesis testing
Purpose:
- test whether the data allow us to reject \(H_0\)
- remember: rejecting \(H_0\) \(\neq\) accepting \(H_A\)
- remember: not rejecting \(H_0\) \(\neq\) \(M_A == M_B\)
- obsession with the p-value
In fact: all we can ever say is whether \(H_0\) was rejected or not!
There are more problems
- we’re bad at interpreting NHST results
- strong assumptions about the data
- no stopping rule (increase n and everything becomes significant)
Hypothesis testing in general
- core of inference testing
- core of scientific endeavour
- think of the ‘reproducibility crisis’
- we want to avoid fishing expeditions
So: we deseperately need hypotheses, but NHST is weak
Enter
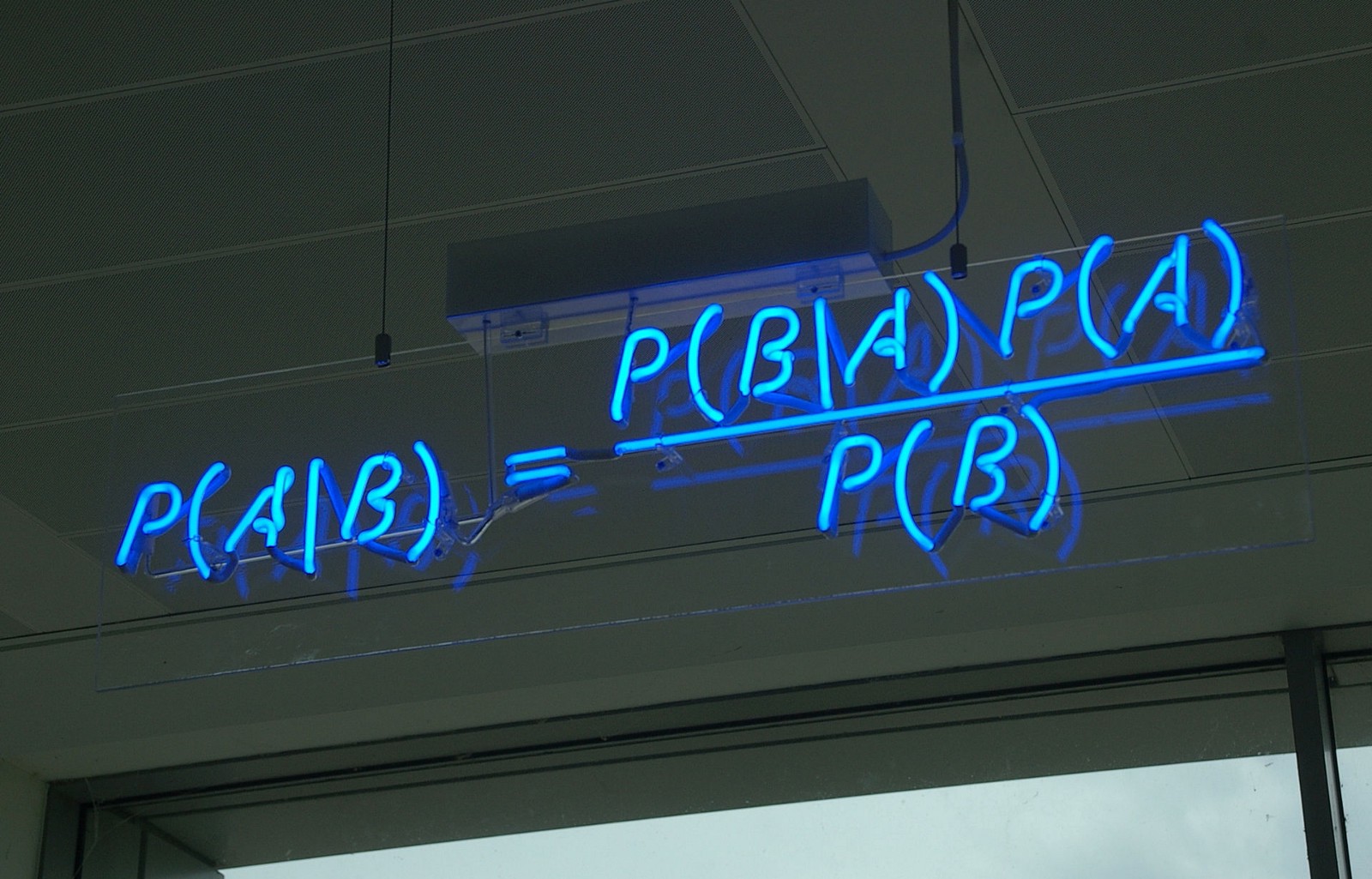
What is it?
Rooted in two ideas of probability:
Frequentist vs Bayesian
Laymen’s explanation
I have misplaced my phone somewhere in the home. I can use the phone locator on the base of the instrument to locate the phone and when I press the phone locator the phone starts beeping.
Problem: Which area of my home should I search?
From this SO post
…
Frequentist Reasoning
I can hear the phone beeping. I also have a mental model which helps me identify the area from which the sound is coming. Therefore, upon hearing the beep, I infer the area of my home I must search to locate the phone.
…
Bayesian Reasoning
I can hear the phone beeping. Now, apart from a mental model which helps me identify the area from which the sound is coming from, I also know the locations where I have misplaced the phone in the past. So, I combine my inferences using the beeps and my prior information about the locations I have misplaced the phone in the past to identify an area I must search to locate the phone.


What is it?
Remember?
\(P(A|B) = \frac{P(B|A)*P(A)}{P(B)}\)
\(P(terrorist|alarm) = \frac{P(alarm|terrorist)*P(terrorist)}{P(alarm)}\)
Translated to hypothesis testing
- \(P(H)\) : prob. that hypothesis H prior to the data
- \(P(D)\) : marginal prob. of the data (same for all hyp.)
- \(P(D|H)\) : compatibility of the data with the hyp. (likelihood)
We want to know:
\(P(H|D)\) : prob. of the hyp. given the data (posterior)
\(P(H|D) = \frac{P(D|H)*P(H)}{P(D)}\)
\(posterior = \frac{likelihood*prior}{marginal}\)
Formally
Since: \(P(D)\) does not involve the hypothesis, …
\(P(H|D) \propto P(D|H)*P(H)\)
Conceptually
\(posterior \propto likelihood*prior\)
- posterior: what we know after having seen the data (i.e. what we learned from the data)
- prior: our prior beliefs
- likelhood: observation
Think for a second
- this means that evidence can/must convince
- if you know that the sun is unlikely to have exploded, the evidence must be very, very strong to convince you otherwise
Bayesian inference: about updating beliefs with the data.
Bayesian hypothesis tests
If for any H:
\(P(H|D) \propto P(D|H)*P(H)\)
… then maybe we can compare the evidence \(P(H_0|D)\) with the evidence \(P(H_A|D)\)?
Bayes factors
Important: no special status for \(H_0\)!
Suppose we have not seen the data, then:
\(odds_{0A} = \frac{P(H_0)}{P(H_A)}\)
or:
\(odds_{prior} = \frac{prior_{H_0}}{prior_{H_A}}\)
Bayes factors
What we want for two hypotheses \(H_0\) and \(H_A\) is:
- \(P(D|H_A)\) : compatibility of the data with \(H_A\)
- … versus …
- \(P(D|H_0)\) : compatibility of the data with \(H_0\)
\(\frac{P(H_A|D)}{P(H_0|D)} = \frac{P(D|H_A)}{P(D|H_0)}*\frac{P(H_A)}{P(H_0)}\)
How much more likely the data are under \(H_A\) compared to \(H_0\).
Called the Bayes Factor \(BF_{A0}\)
The evidence in the data favors one hypothesis, relative to another, exactly to the degree that the hypothesis predicts the observed data better than the other.
Stepwise example
Suppose we have two lines of thought re. successful re-integration after prison:
- Optimists
- Skeptics
Optimists say that 65% of offenders can be re-integrated in society; skeptics say it’s 40%.
Data: 100 offenders and their outcome (successful vs fail)
- \(H_{optimists} = 0.65\)
- \(H_{skeptics} = 0.40\)
Now the data come in
- 100 ex-prisoners
- 58 successfully re-integrated in society
- 42 not
- \(58/100 = 0.58\)
Closer to the optmists, but how much?
Relative weight of evidence
How much does the evidence change our beliefs?
Plausibility of the hypotheses \(H_{opt.} = 0.65\) and \(H_{skept.} = 0.40\) changes according to Bayes’ rule!
Probability of observations
Probability of observations
58 successes:
- for \(H_{opt.} = 0.65\) = 0.0284
for \(H_{skept.} = 0.40\) = 0.0001
So: \(\frac{H_{opt.}}{H_{skept.}} = \frac{0.0284}{0.0001} = 250.03\)
Bayes factor
\(BF = \frac{P(D|H_{opt.})}{P(D|H_{skept.})} = 250.03\)
The data are 250 times more likely under \(H_{opt.}\) than under \(H_{skept.}\)
But what about uncertain priors?
Prior beliefs as distributions
- rather than specific point estimates, we use distributions
- \(H_{optimists}\) becomes a distribution (here normal distr.)
- \(H_{skeptics}\) becomes a distribution (here normal distr.)
Bayesian estimation can handle this.
What can it solve?
What can it solve?
- all hypothesis testing questions!
- those with uncertainty
- aaaaand ….
What can it solve?
It can solve the sh** \(H_0\) problem!!!!!
Now we can quantify relative evidence:
\(BF_{01} = \frac{P(H_0|D)}{P(H_1|D)}\)
Relative evidence of \(H_0\) over \(H_1\)
Why should I care?
Why should I care?

Why should I care?
- Bayesian framework widely considered superior
- Bayesian logic fits with “science” better than NHST
- tools problem is overcome
- will become standard in the future
How do I do it?
How do I do it?
Two approaches in PSM2:
How do I do it?
Is there a difference?
tapply(mydata$score, mydata$group, mean)## A B
## 101.2419 100.6370- \(H_0\) : \(M_A \approx M_B\)
- \(H_1\) : \(M_A \neq M_B\)
Old school NHST
t.test(score ~ group
, data = mydata
, var.eq=TRUE)##
## Two Sample t-test
##
## data: score by group
## t = 0.90114, df = 1998, p-value = 0.3676
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.7115953 1.9214737
## sample estimates:
## mean in group A mean in group B
## 101.2419 100.6370Effect size
Cohen’s d
d = 0.90*(sqrt(1/1000 + 1/1000))
d## [1] 0.04024922BayesFactor R
library(BayesFactor)
ttestBF(formula = score ~ group
, data = mydata)## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 0.07520633 ±0%
##
## Against denominator:
## Null, mu1-mu2 = 0
## ---
## Bayes factor type: BFindepSample, JZSBayesFactor R
\(BF_{10} = 0.075\), so:
\(BF_{01} = 1/0.075 = 13.33\)
–> Evidence quantified for both hypotheses!
Interpreting BFs

How do I do it?
JASP

JASP

JASP

JASP


Tutorial
- Bayesian hypothesis testing in practice
- use R and JASP
Next week
- Q&A session
- final questions before exam