PSM1 recap and outlook
PSM2 UCL
Bennett Kleinberg
8 Jan 2019
Welcome
Probability, Statistics & Modeling II
Lecture 1
Quick recap 1
Predicting crimes

Predicting crimes
Behind the problem:
What is the claim?
Formalising the problem
chance_day_1 = 0.5
chance_day_2 = 0.5
chance_day_3 = 0.5
#...Solving the problem
Probability for correct prediction?
P(prediction == 1) = p_correct = 0.5
… on 10 consecutive days?
p_correct * p_correct * p_correct ...
p_correct = 0.5
# for d = 10 days
d = 10
#Formal:
p_correct ^ d## [1] 0.0009765625Equivalent to: 1/2^10 = 1/1024
MARGINAL Probability:
P(EVENT)
Even very, very, rare events happen…
… but most of the time they don’t.


You need probability theory to tell the lucky from the likely.
(and proper statistics notations)
Quick recap 2
About Maria
Maria is 26 years old, single, outspoken, and very bright. She majored in law. As a student, she was deeply concerned with issues of discrimination and miscarriage of justice, and also participated in animal-rights demonstrations.
Adapted from Tversky & Kahneman (1983)
Which is more probable?
- A: Maria works in a law firm
- B: Maria works in a law firm and does pro bono work for disadvantaged defendants
Formalising the problem
Two events:
- P(A) #prob of answer A
- P(B) #prob of answer B
… BUT:
There’s something special with P(B)
P(B) = P(A) + "something else"
P(B) contains two ‘events’: P(A) and ‘pro bono work’
Let 'pro bono work' be P(C)
P(B) = P(A) and P(C)
Solving the problem
Joint probability
P(B) = P(A and C)
Let’s try:
Prob_A = 0.4
Prob_C = 0.3Formula: P(A and B) = P(A)*P(C)
(Prob_A_and_C = Prob_A * Prob_C)## [1] 0.12By definition: P(X) > P(X and Y)
Therefore:
P(‘M is a lawyer’) > P(‘M is a lawyer’ and ‘pro-bono work’)
JOINT Probability:
P(EVENT_A AND EVENT_B) = P(EVENT_A)*P(EVENT_B)
Probability of two independent events is always smaller than the probability of each single events.

Quick recap 3
Screening terrorists

Your turn
What are the chances that this man is a terrorist?

Formalising the problem
CONDITIONAL Probability:
Probability of TERRORIST given that there is an ALARM
Looking for: P(terrorist GIVEN alarm)
Formal: P(terrorist|alarm)
Solving the problem (method 1)
| Terrorist | Passenger | ||
|---|---|---|---|
| Terrorist | 950 | 50 | 1,000 |
| Passenger | 4,950 | 94,050 | 99,000 |
| 5,900 | 94,100 | 100,000 |
P(terrorist|alarm) = 950/5900 = 16.10%
Solving the problem (method 2)
Bayes’ rule
Setting the stage:
- P(T) -> probability of terrorist
- P(A) -> probability of alarm
We want:
- P(T|A)
We know:
- accuracy = P(A|T) = 0.95
- baserate = P(T) = 0.01
Bayes’ rule (cont’d)
accuracy = 0.95 #P(A|T)
baserate = 0.01 #P(T)Bayes’ rule: P(T|A) = ( P(A|T) * P(T) ) / P(A)
P(A) –> probability of any alarm???
P(A) = P(A|T) * P(T) + P(A|notT) * P(notT)
(Prob_notT = 1 - baserate) #P(notT) = 1 - P(T)## [1] 0.99(Prob_A_given_notT = 1 - accuracy) #P(A|notT) = 1 = P(A|T)## [1] 0.05Bayes’ rule (cont’d)
Putting it together:
#Bayes' rule:
Prob_A = accuracy * baserate + Prob_A_given_notT * Prob_notT #P(A) = P(A|T) * P(T) + P(A|notT) * P(notT)
Prob_A## [1] 0.059Prob_T_given_A = (accuracy * baserate) / Prob_A #P(T|A) = ( P(A|T) * P(T) ) / P(A)
Prob_T_given_A## [1] 0.1610169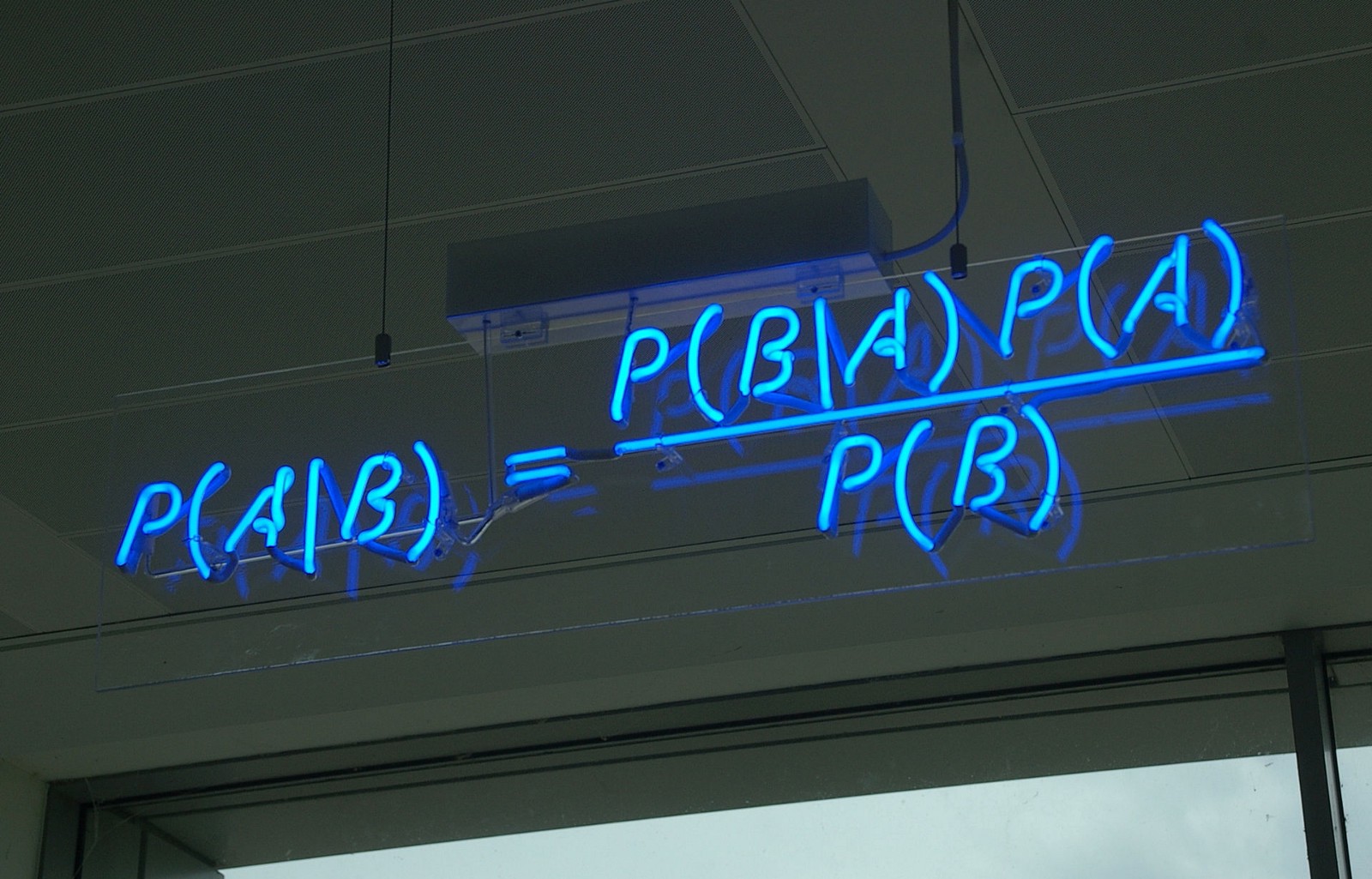
! Revise this rule here
CONDITIONAL Probability:
P(EVENT_A GIVEN EVENT_B) = P(EVENT_A|EVENT_B)
Probability of one event given that another event is true.
BEWARE OF THE BASERATE FALLACY
Quick recap 4
Solving gang crime

The context
Problem: gang crime in London
Mayor proposes two programmes:
- A: zero-tolerance
- B: work-and-integration
100 gang-members in two areas.
Outcome measure: number of gang members who disengaged
Results
| Programme A | Programme B | |
|---|---|---|
| Camden | 63/90 | 8/10 |
| Lambeth | 4/10 | 45/90 |
Mayor has GBP 5m to invest in one programme.
Your decision?
Solving the problem
| Programme A | Programme B | |
|---|---|---|
| Camden | 63/90 = 70% | 8/10 = 80% |
| Lambeth | 4/10 = 40% | 45/90= 50% |
| 67/100 = 67% | 53/100 = 53% |
[a] phenomenon wherein an association or a trend observed in the data at the level of the entire population disappears or even reverses when data is disaggregated by its underlying subgroups Alipourfard et al., 2018
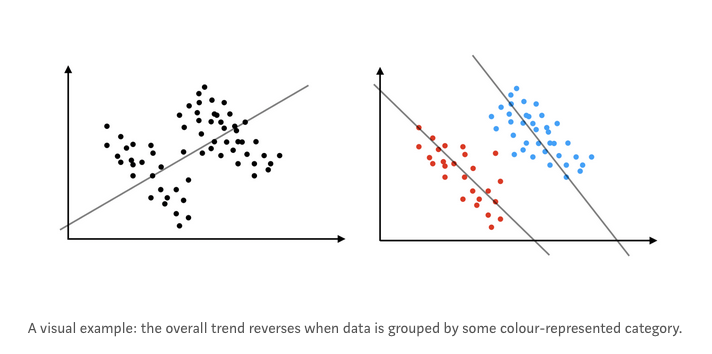
BEWARE OF THE CONTEXT OF YOUR DATA
10 min. break
This module
Aim
- go beyond PSM I
- understand more complex data
- model data and make inferences
- make sense of crime data
More on learning outcomes in the module handbook
Tools we’ll use


- open-source + free
- wide support community (e.g., on Stackoverflow)
- made for statistics
- state-of-the-art libraries
But still…
- R grows fast
- Highly desirable/required in industry (Google, Facebook, Microsoft, Amazon, …)
Structure of the module
- 9 Lectures (Tuesdays, 14-16h)
- 5 Tutorials (alternating Tuesdays, 10-12h)
Teaching assistant: Isabelle van der Vegt
Assessment
- Class test
- Applied Crime Analysis Project
Class test
- 50% of final grade
- 1-hour closed-book exam
- 8 open questions & MC questions
- Date: 19 Mar 2019, 14-16h, (details)
Applied Crime Analysis Project
- 50% of final grade
- apply skills on dataset
- address a research question
- demonstrate open science practices
- Due: 29 Mar 2019 (details)
Outlook
- The Generalised Linear Model
- Non-parametric data + discrete data
- Open Science lab
- Statistical evidence
- Bayesian statistics
What’s next?
Homework for today:
Next week:
Tutorial + lecture
Tutorial: Refresher of PSM I with R + GLM tutorial