MMiDS 5.6: Self-Assessment Quiz

In a stochastic blockmodel (SBM), what does \( b_{i,j} \) represent?

• a) The probability that vertex \( i \) is assigned to block \( j \).
• b) The probability that there is an edge between any two vertices.
• c) The probability that there is an edge between a vertex in block \( C_i \) and a vertex in block \( C_j \).
• d) The weight of the edge between vertex \( i \) and vertex \( j \).

In the symmetric stochastic blockmodel (SSBM), the second eigenvector of the expected Laplacian matrix \( L := \mathbb{E}[L] \) is given by:

• a) \( q_1 = \frac{1}{\sqrt{n}} \mathbf{1}_n \)
• b) \( q_2 = \frac{1}{\sqrt{n}} \begin{pmatrix} \mathbf{1}_{n/2} \\ -\mathbf{1}_{n/2} \end{pmatrix} \)
• c) \( q_3, \ldots, q_n \), which form an orthonormal basis of \( (\mathrm{span}\{q_1, q_2\})^\perp \)
• d) None of the above.

Which of the following matrices encodes the block assignments in a stochastic blockmodel?

• a) \( M \)
• b) \( B \)
• c) \( Z \)
• d) \( A \)

Which of the following statements about the eigenvalues of the expected Laplacian matrix \( L := \mathbb{E}[L] \) in the symmetric stochastic blockmodel (SSBM) is true?

• a) \( \lambda_1 = 0 \) and \( \lambda_2 = qn \), where \( q \) is the inter-block connection probability.
• b) \( \lambda_1 = pn \) and \( \lambda_2 = 0 \), where \( p \) is the intra-block connection probability.
• c) \( \lambda_1 = \frac{p+q}{2}n \) and \( \lambda_2 = \frac{p-q}{2}n \).
• d) \( \lambda_1 = \frac{p-q}{2}n \) and \( \lambda_2 = \frac{p+q}{2}n \).

Consider an Erdős-Rényi (ER) random graph with \( n \) vertices and edge probability \( p \). The expected number of edges in the graph is:

• a) \( n^2p \)
• b) \( \binom{n}{2}p \)
• c) \( np \)
• d) \( n(n-1)p \)

What is the expected number of triangles in an Erdős-Rényi random graph \( G(n, p) \)?

• a) \( \binom{n}{3} p^2 \)
• b) \( \binom{n}{2} p^3 \)
• c) \( \binom{n}{3} p^3 \)
• d) \( \binom{n}{2} p^2 \)

Consider the following Python code snippet:

import networkx as nx
import numpy as np

n = 5
p = 0.4
seed = 123
rng = np.random.default_rng(seed)

G = nx.Graph()
G.add_nodes_from(range(n))
for i in range(n):
    for j in range(i + 1, n):
        if rng.random() < p:
            G.add_edge(i, j)

nx.draw(G, with_labels=True, node_size=500, font_size=12, font_color='white')

Which of the following best describes the graph generated by this code?

• a) An Erdős-Rényi (ER) random graph with \( n=5 \) vertices and edge probability \( p=0.4 \).
• b) A stochastic blockmodel (SBM) with \( n=5 \) vertices and intra-block probability \( p=0.4 \).
• c) A symmetric stochastic blockmodel (SSBM) with \( n=5 \) vertices and inter-block probability \( p=0.4 \).
• d) An inhomogeneous Erdős-Rényi (ER) random graph with \( n=5 \) vertices and edge probabilities given by a matrix \( M \).

Consider the following graph generated using NetworkX in Python:

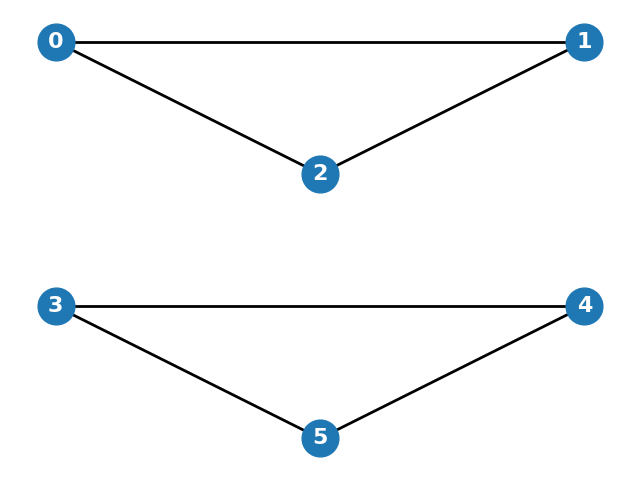
Which of the following models could have produced this graph?

• a) An Erdős-Rényi (ER) random graph.
• b) A stochastic blockmodel (SBM) with two communities.
• c) A symmetric stochastic blockmodel (SSBM) with two communities.
• d) All of the above.

Which of the following is true for the spectral properties of a symmetric stochastic blockmodel (SSBM)?

• a) The matrix has rank 1.
• b) The eigenvalues are all equal.
• c) The matrix can be decomposed into orthogonal eigenvectors with corresponding eigenvalues.
• d) The eigenvalues are purely imaginary.

In the stochastic blockmodel, what happens to the difficulty of recovering the community structure if the inter-block connection probability \( b_{1,2} \) is close to the intra-block connection probability \( b_{1,1} \)?

• a) It becomes easier.
• b) It remains unchanged.
• c) It becomes harder.
• d) None of the above.