MMiDS 5.5: Self-Assessment Quiz

Which of the following best describes the 'cut ratio' of a graph cut \((S, S^c)\)?

• a) The ratio of the number of edges between \(S\) and \(S^c\) to the total number of edges in the graph.
• b) The ratio of the number of edges between \(S\) and \(S^c\) to the size of the smaller set, \(\min\{|S|, |S^c|\}\).
• c) The ratio of the number of edges within \(S\) to the number of edges within \(S^c\).
• d) The ratio of the total number of edges in the graph to the number of edges between \(S\) and \(S^c\).

What is the isoperimetric number (or Cheeger constant) of a graph \(G\)?

• a) The largest value of the cut ratio over all possible cuts.
• b) The smallest value of the cut ratio over all possible cuts.
• c) The average value of the cut ratio over all possible cuts.
• d) The median value of the cut ratio over all possible cuts.

What does the Cheeger Inequality establish?

• a) A relationship between the isoperimetric number and the largest Laplacian eigenvalue.
• b) A relationship between the isoperimetric number and the second largest Laplacian eigenvalue.
• c) A relationship between the isoperimetric number and the smallest Laplacian eigenvalue.
• d) A relationship between the isoperimetric number and the second smallest Laplacian eigenvalue.

Given a graph \(G\) with \(n\) vertices and maximum degree \(\bar{\delta}\), what is the range of the second smallest Laplacian eigenvalue \(\mu_2\) according to the Cheeger Inequality?

• a) \(\frac{\phi_G^2}{2\bar{\delta}} \leq \mu_2 \leq 2\phi_G\)
• b) \(\frac{\phi_G^2}{2\bar{\delta}} \leq \mu_2 \leq \phi_G\)
• c) \(\frac{\phi_G}{2\bar{\delta}} \leq \mu_2 \leq 2\phi_G^2\)
• d) \(\frac{\phi_G}{2\bar{\delta}} \leq \mu_2 \leq \phi_G^2\)

In the context of spectral graph theory, what is the Fiedler vector?

• a) The eigenvector associated with the largest eigenvalue of the Laplacian matrix.
• b) The eigenvector associated with the smallest eigenvalue of the Laplacian matrix.
• c) The eigenvector associated with the second smallest eigenvalue of the Laplacian matrix.
• d) The eigenvector associated with the second largest eigenvalue of the Laplacian matrix.

In the graph-cutting algorithm based on the Fiedler vector, how is the graph embedded in \(\mathbb{R}\)?

• a) Each vertex \(i\) is mapped to the corresponding entry \(y_{1,i}\) of the first eigenvector.
• b) Each vertex \(i\) is mapped to the corresponding entry \(y_{2,i}\) of the second eigenvector.
• c) Each vertex \(i\) is mapped to the sum of the corresponding entries of the first and second eigenvectors.
• d) Each vertex \(i\) is mapped to the difference between the corresponding entries of the first and second eigenvectors.

What is the range of possible cuts considered by the graph-cutting algorithm based on the Fiedler vector?

• a) All possible cuts of the graph.
• b) Only cuts of the form \((S_k, S_k^c)\), where \(S_k = \{\pi(1), \ldots, \pi(k)\}\) for \(k \leq n-1\).
• c) Only cuts of the form \((S_k, S_k^c)\), where \(S_k = \{\pi(1), \ldots, \pi(k)\}\) for \(k \leq n/2\).
• d) Only cuts of the form \((S_k, S_k^c)\), where \(S_k = \{\pi(1), \ldots, \pi(k)\}\) for \(k \leq \sqrt{n}\).

Consider the following graph:

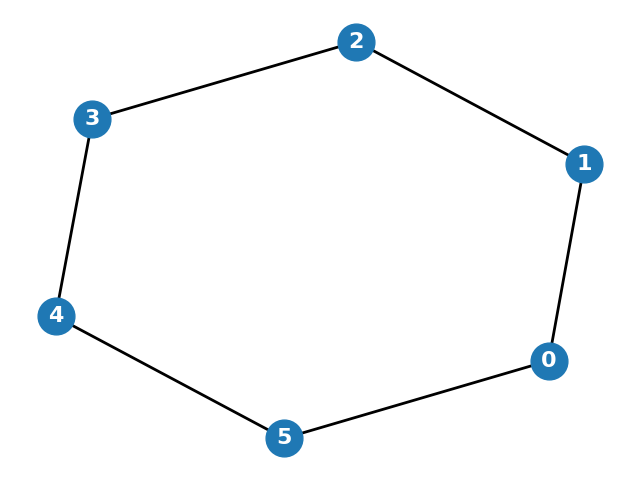
What is the isoperimetric number (Cheeger constant) of this graph?

• a) 1/6
• b) 1/3
• c) 1/2
• d) 2/3

What is the main advantage of the graph-cutting algorithm based on the Fiedler vector compared to finding the cut that minimizes the cut ratio directly?

• a) The Fiedler vector-based algorithm always finds the optimal cut.
• b) The Fiedler vector-based algorithm is computationally tractable, while minimizing the cut ratio directly is NP-hard.
• c) The Fiedler vector-based algorithm can handle weighted graphs, while minimizing the cut ratio directly cannot.
• d) The Fiedler vector-based algorithm can handle directed graphs, while minimizing the cut ratio directly cannot.

What is the minimum bisection problem?

• a) Finding a cut of a graph that minimizes the number of edges across the cut.
• b) Finding a cut of a graph that divides the vertices into two equal-sized sets and minimizes the number of edges across the cut.
• c) Finding a cut of a graph that maximizes the number of edges across the cut.
• d) Finding a cut of a graph that divides the vertices into two equal-sized sets and maximizes the number of edges across the cut.

Which of the following is the relaxation of the minimum bisection problem presented in the text?

• a) \(\min \frac{1}{4} \left\{\sum_{\{i,j\} \in E} (x_i - x_j)^2 : x = (x_1, ..., x_n)^T \in \mathbb{R}^n, \sum_{i=1}^n x_i = 0, \sum_{i=1}^n x_i^2 = n\right\}\)
• b) \(\min \frac{1}{4} \left\{\sum_{\{i,j\} \in E} |x_i - x_j| : x = (x_1, ..., x_n)^T \in \mathbb{R}^n, \sum_{i=1}^n x_i = 0, \sum_{i=1}^n x_i^2 = n\right\}\)
• c) \(\max \frac{1}{4} \left\{\sum_{\{i,j\} \in E} (x_i - x_j)^2 : x = (x_1, ..., x_n)^T \in \mathbb{R}^n, \sum_{i=1}^n x_i = 0, \sum_{i=1}^n x_i^2 = n\right\}\)
• d) \(\max \frac{1}{4} \left\{\sum_{\{i,j\} \in E} |x_i - x_j| : x = (x_1, ..., x_n)^T \in \mathbb{R}^n, \sum_{i=1}^n x_i = 0, \sum_{i=1}^n x_i^2 = n\right\}\)

In the proof of the easy direction of Cheeger's Inequality (\(\mu_2 \leq 2\varphi_G\)), how is the test vector \(x\) constructed?

• a) It is chosen randomly.
• b) It is the Fiedler vector.
• c) It takes one value on the set \(S\) and a different value on its complement \(S^c\).
• d) It is the indicator vector of the set \(S\).