Concurrent Programming

Parallelism

Parallel execution with immutable data

Algorithms that can be executed in a functional immutable style
are simpler to parallelize because the lack of share, mutable state.

Some examples:

• Evaluation of expressions
• Sorting
• Operating on lists or matrices
• Functional programming HOFs like map, fold, etc.
• Computing primes, and more

Math Expressions

If I want to calculate:

In can do in parallel:

And:

And then multiply the results

Implementation in Rust sequential

use std::thread;

fn evaluate_sequential(k: f64, a: f64, t: f64) -> f64 {

    let a = 2.0 * k * a * t;
    let b = f64::exp(-a * t * t);
    
    return a * b;
}

Implementation in Rust Parallel

Quite simple because join returns the result of the expression.

use std::thread;

fn evaluate_parallel(k: f64, a: f64, t: f64) -> f64 {

    let thread1 = thread::spawn(
        || 2.0 * k * a * t
    );
    let thread2 = thread::spawn(
        || f64::exp(-a * t * t)
    );

    let a = thread1.join().unwrap();
    let b = thread2.join().unwrap();
    
    return a * b;
}

Implementation in Java

• A little more complex because join doesn't return anything.
• So we need to simulate that in some way
• Let's inherit from Thread and add that behaviour

public class MathThread extends Thread {
    private final Supplier<Double> expression;
    private double result;

    public MathThread(Supplier<Double> expression) {
        this.expression = expression;
    }
    
    public void run() {
        // When running the thread save the result
        result = expression.get();
    }
    
    public double getValue() { return result; }
}

Implementation in Java - Parallel evaluation

double evaluateParallel(double k, double a, double t) throws InterruptedException {
    
        var thread1 = new MathThread(() -> 2* k * a * t);
        var thread2 = new MathThread(() -> Math.exp(-a * t * t));
      
        thread1.start(); // Start thread1
        thread2.start(); // Start thread2
      
        // Wait for both threads to complete
        thread1.join();
        thread2.join();
      
        // Now get the values and multiply them
        return thread1.getValue() * thread2.getValue();
 }

Matrix Operations

Matrix definition

#[derive(Debug, Clone)]
pub struct Matrix(pub Vec<Vec<f64>>);

impl Matrix {
    pub fn rows(&self) -> usize { self.0.len() }
    pub fn columns(&self) -> usize { self.0[0].len() }
}

Add Matrices

Serial Version

    pub fn add_serial(&self, other: &Matrix) -> Matrix {
        let rows = self.rows();
        let cols = self.columns();
        let mut result = Vec::new();

        for i in 0..rows {
            let mut row = Vec::new();
            for j in 0..cols {
                row.push(self.0[i][j] + other.0[i][j]);
            }
            result.push(row);
        }
        Matrix(result)
    }

Using map

pub fn add_serial(&self, other: &Matrix) -> Matrix {
    let rows = self.rows();
    let cols = self.columns();
    let result = (0..rows)
        .map(|i|
            (0..cols)
                .map(|j| self.0[i][j] + other.0[i][j])
                .collect()
        )
        .collect();
    Matrix(result)
}

Parallel Version, Row by Row

pub fn add_parallel(&self, other: &Matrix) -> Matrix {
    let rows = self.rows();
    let cols = self.columns();

    thread::scope(|s| {
        let threads: Vec<_> = (0..rows)
            .map(|i| {
                s.spawn(move || {
                    (0..cols).map(|j| self.0[i][j] + other.0[i][j]).collect()
                })
            })
            .collect();

        Matrix(threads.into_iter()
            .map(|t| t.join().unwrap())
            .collect())
    })
}

Merge Sort

Algorithm

• If the array has 1 or fewer elements it's already sorted
• Else:
  • Split the array in 2 parts and recursively apply mergesort to each of the parts
  • Merge the two already sorted parts

Sequential implementation

pub fn sort(array: &[i32]) -> Vec<i32> {
    let len = array.len();
    if len <= 1 {
        array.to_vec()
    }
    else {
        let x = sort(&array[..len/2]); // <-- array slice
        let y = sort(&array[len/2..]);
        merge(&x, &y)
    }
}

Merge

pub fn merge(first: &[i32], second: &[i32]) -> Vec<i32>{
    let mut result = Vec::new();
    let mut i = 0; let mut j = 0;
    
    // Merge until one of the inputs is exhausted
    while i < first.len() && j < second.len() {
        if first[i] <= second[j] {
            result.push(first[i]);
            i += 1
        } else {
            result.push(second[j]);
            j += 1
        }
    }
    // Copy the remaining items
    result.extend_from_slice(&first[i..]);
    result.extend_from_slice(&second[j..]);
    result
}

Parallel Implementation

• Recursively sort the two halves of the array in parallel
• Sequentially merge the two halves of the array

Parallel Implementation

pub fn sort(array: &[i32]) -> Vec<i32> {
    let len = array.len();
    if len <= 1 {
        array.to_vec()
    }
    else {
        let (first, second) = thread::scope(|s| {
            let x = s.spawn(|| sort(&array[..len / 2]));
            let y = s.spawn(|| sort(&array[..len / 2]));
            (x.join().unwrap(), y.join().unwrap()) // <-- Scope also returns a value
        });
        merge(&first, &second)
    }
}

Parallel implementation - Using fewer threads

{
    let x = s.spawn( || sort( & array[..len / 2]));
    let y = s.spawn( || sort( & array[..len / 2]));
    (x.join().unwrap(), y.join().unwrap())
}

{
    let x = s.spawn(|| sort(&array[..len / 2]));
    let y = sort(&array[..len / 2]);
    (x.join().unwrap(), y)
});

Merge Sort

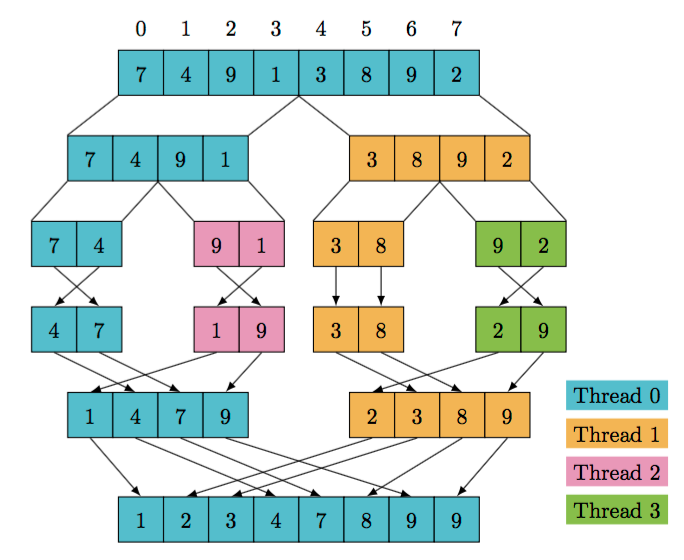
The right and the wrong way

{
    let x = s.spawn(|| sort(&array[..len / 2]));
    let x_value = x.join().unwrap()
    let y_value = sort(&array[..len / 2]);
    (x_value, y_value)
});

{
    let x = s.spawn(|| sort(&array[..len / 2]));
    let y_value = sort(&array[..len / 2]);
    let x_value = x.join().unwrap()
    (x_value, y_value)
});

Let's try it

• Bad Result: 9 ms vs 450 ms
• Why?
• Too many Context Switches
• Processor caches: Cache levels, for example:
  • L1, L2 & L3
  • L1 is private to each core
  • L2 & L3 are shared.

Using a limit.

Do not parallelize if the size of the array is below a certain value.

For example if we put a limit of 1000 items:

Serial Sort: 7.172755ms
Parallel Sort: 1.682205ms