07 - ЕКСПОНЕНЦІАЛЬНЕ ЗГЛАДЖУВАННЯ

Прогнозування часових рядів

Ігор Мірошниченко

КНЕУ::ІІТЕ

11/9/22

Експоненціальне згладжування: концепція

Історична довідка

Розроблено в 1950-х і 1960-х роках як методи (алгоритми) для створення точкових прогнозів.
Об’єднує «рівень», «тренд» і «сезонну» компоненти для опису часових рядів.
Швидкість зміни компонентів контролюється «параметрами згладжування»: $\alpha$, $\beta$ і $\gamma$ відповідно.
Необхідно вибрати оптимальні значення для параметрів згладжування (та початкових значеннь).
Сучасні моделі ETS (error-trend-seasonal), розроблені в 1990-х і 2000-х роках.

Головна ідея: контроль за швидкістю зміни

$\alpha$ контролює зміну рівнів часового ряду

Якщо $\alpha = 0$, рівні ніколи не оновлюються (середній)
Якщо $\alpha = 1$, рівні оновлюються повністю (наївно)

$\beta$ контролює зміну тренду

Якщо $\beta = 0$, тренд є лінійним
Якщо $\beta = 1$, тренд змінюється для кожного спостереження

$\gamma$ контролює зміну сезонності

Якщо $\gamma = 0$, сезонність фіксована (середня сезонність)
Якщо $\gamma = 1$, сезонність повністю оновлюється (наївна сезонність)

Модель для рівнів, тредну та сезонності

Нам потрібна модель, яка визначає рівень $(\ell_t)$, тренд $(b_t)$ і сезонність $(s_t)$.

Як поєднати ці елементи?

Адитивно? \[y_t = \ell_{t-1} + b_{t-1} + s_{t-m} + \varepsilon_t\]

Мультиплікативно? \[y_t = \ell_{t-1}b_{t-1}s_{t-m}(1 + \varepsilon_t)\]

Може поєднаємо все? \[y_t = (\ell_{t-1} + b_{t-1}) s_{t-m} + \varepsilon_t\]

Як рівень, тренд та сезонність змінюються з часом?

ETS моделі

Форма запису E T S : ExponenTialSmoothing

$\nearrow$ $\uparrow$ $\nwarrow$
Error Trend Season

Error: Адитивні ("A") або мультиплікативні ("M")

Trend: Відсутній ("N"), адитивний ("A"), мультиплікативний ("M") або демпфований ("Ad" або "Md").

Seasonality: Відсутній ("N"), адитивна ("A") or мультиплікативна ("M")

Просте експоненціальне згладжування (SES)

Прості методи

Часовий ряд $y_1, y_2, \dots, y_T$

Наїваний метод (naive) \[\hat{y}_{T+h|T} = y_T\]

На основі середнього (average) \[\hat{y}_{T+h|T} = \frac1T\sum_{t=1}^T y_t\]

Хочете щось середнє між цими методами.
Останні дані повинні мати більшу вагу.

Просте експоненціальне згладжування

Рівняння: \[\hat{y}_{T+1|T} = \alpha y_T + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^2 y_{T-2}+ \cdots\] де $0 \le \alpha \le 1$

Спостереження	$\alpha = 0.2$	$\alpha = 0.4$	$\alpha = 0.6$	$\alpha = 0.8$
$y_t$	0.2	0.4	0.6	0.8
$y_{t-1}$	0.16	0.24	0.24	0.16
$y_{t-2}$	0.128	0.144	0.096	0.032
$y_{t-3}$	0.1024	0.0864	0.0384	0.0064
$y_{t-4}$	0.0819	0.0518	0.0154	0.0013
$y_{t-5}$	0.0655	0.0311	0.0061	0.0003

Просте експоненціальне згладжування

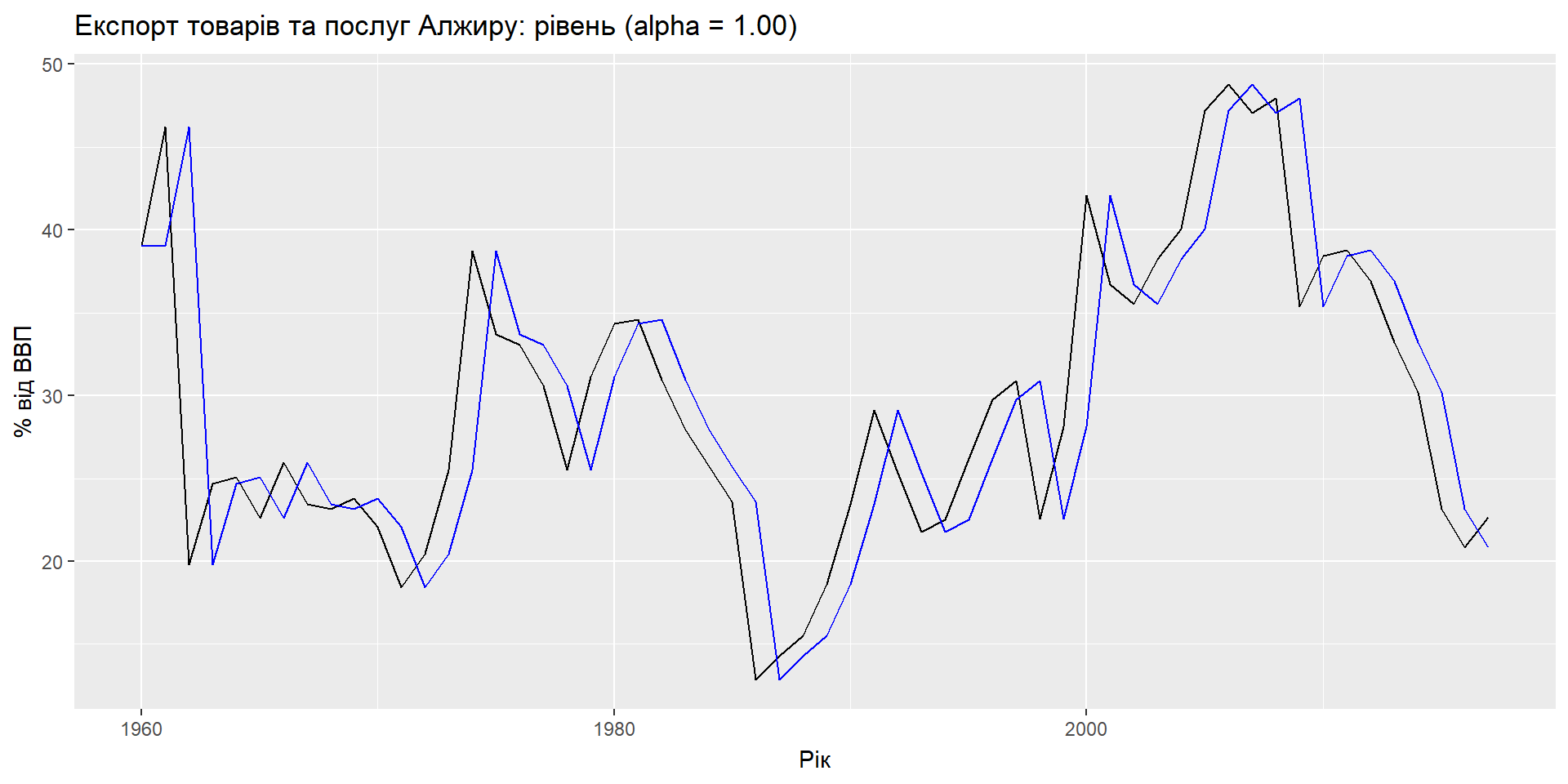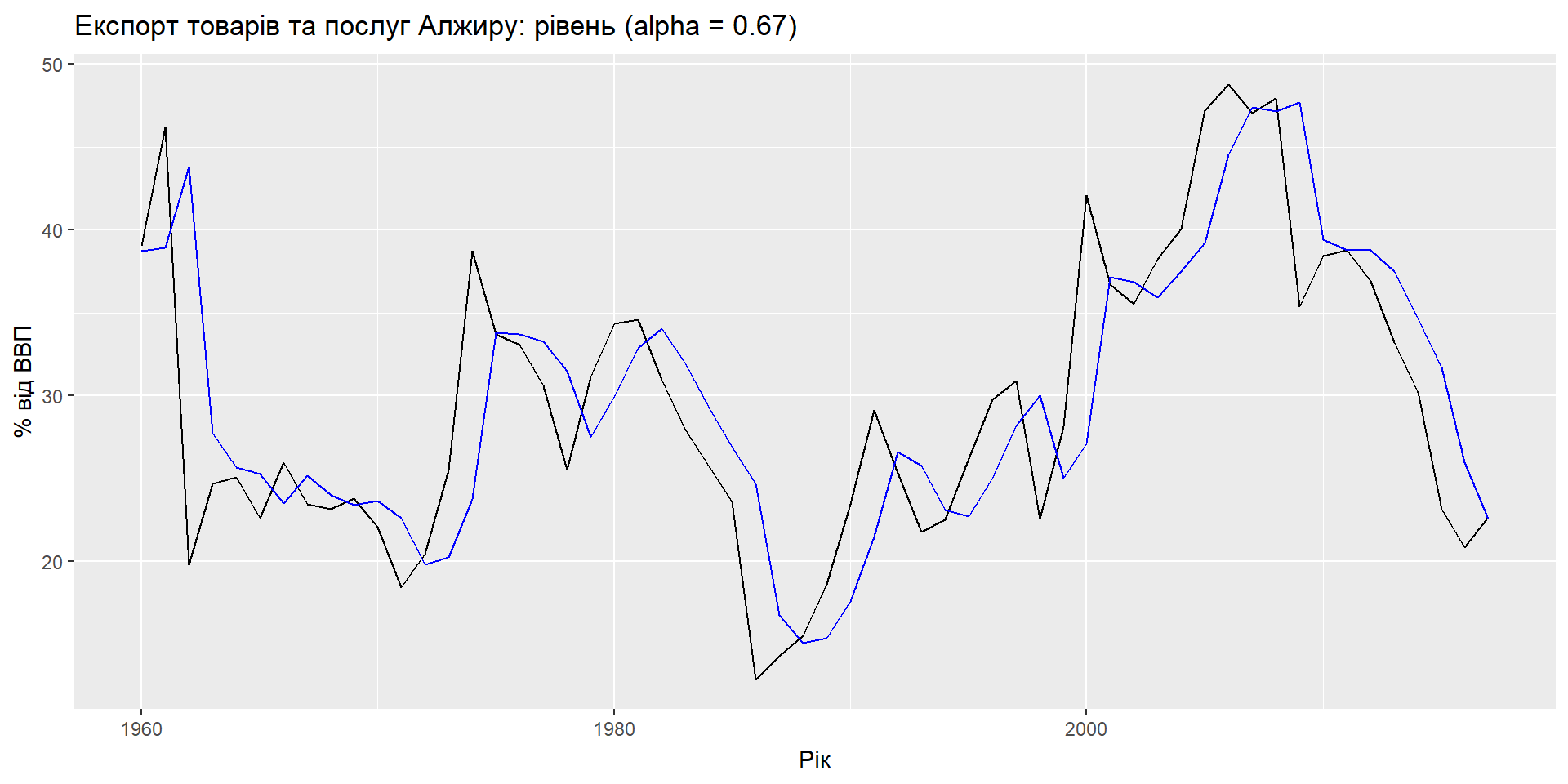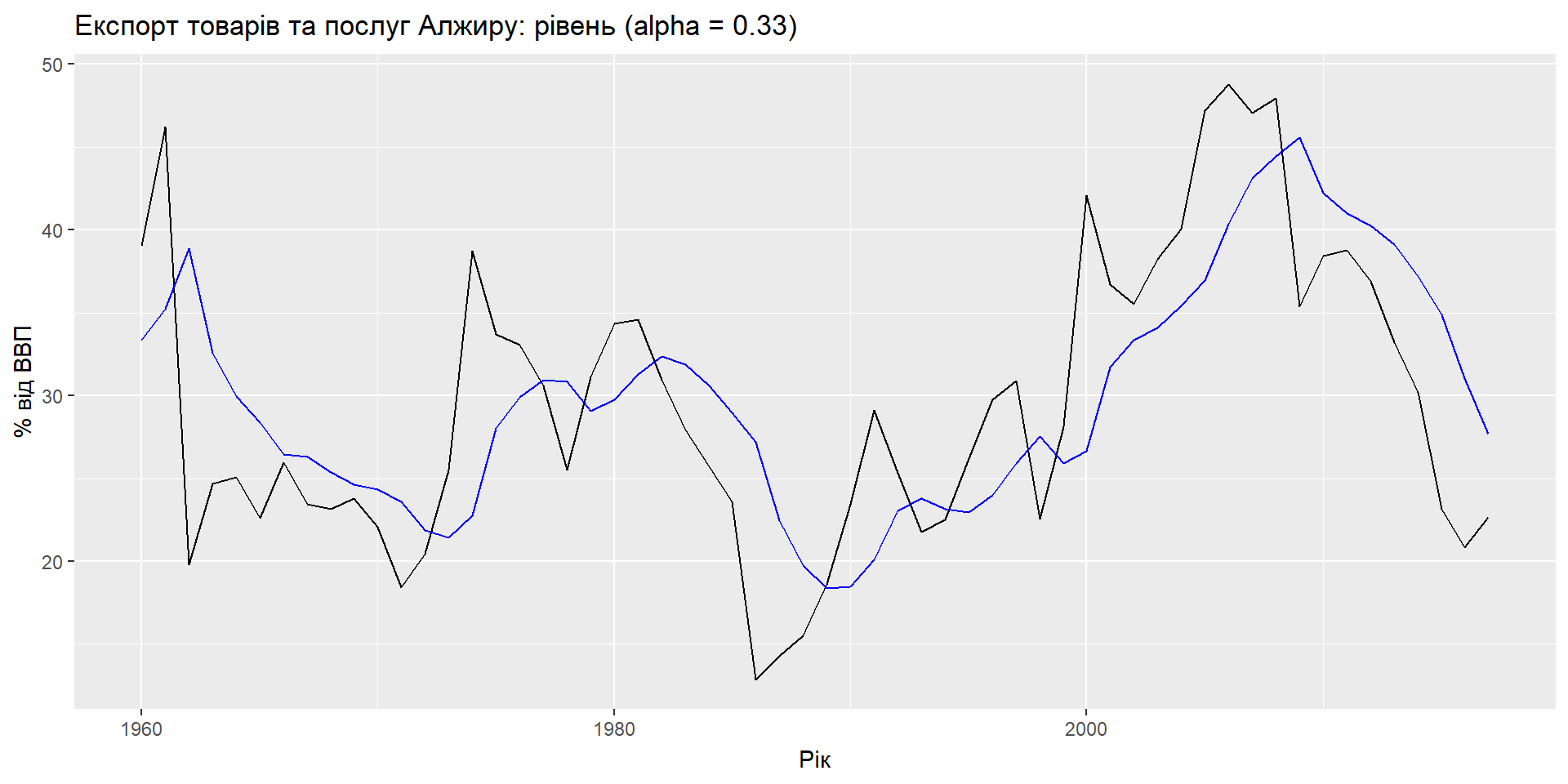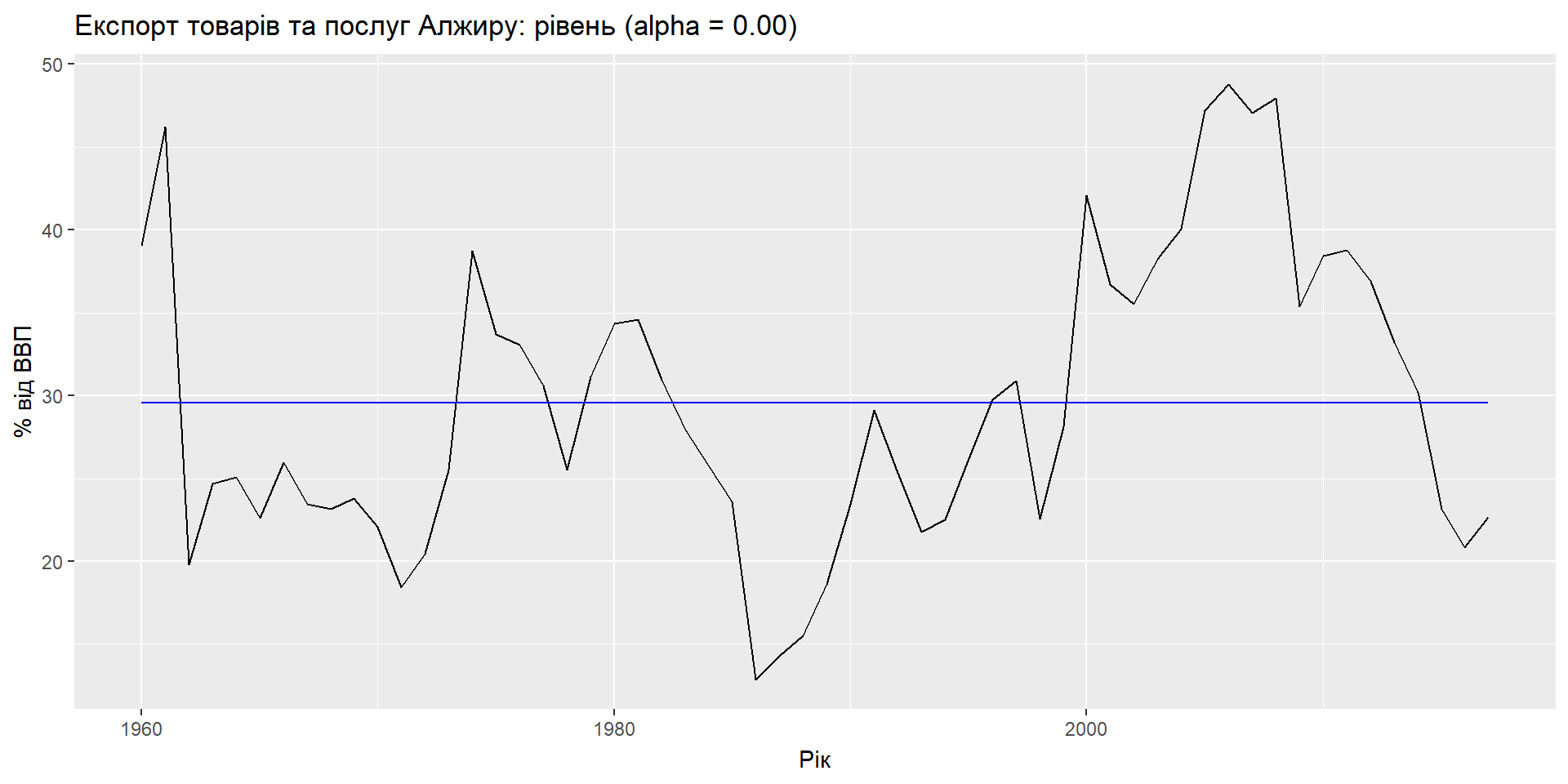
Компоненти

Формула прогнозу: $\hat{y}_{t+h|t} = \ell_{t}$

Формула згладжування: $\ell_{t} = \alpha y_{t} + (1 - \alpha)\ell_{t-1}$

$\ell_t$ – це рівень (або згладжене значення) ряду в момент часу t.
$\hat{y}_{t+1|t} = \alpha y_t + (1-\alpha) \hat{y}_{t|t-1}$

SES має “плоску” функцію прогнозу: \[\hat{y}_{T+h|T} = \hat{y}_{T+1|T} = \ell_{T}, \quad h = 2,3,\dots\] > Такі прогнози будуть придатними лише в тому випадку, якщо часовий ряд не має тенденційної чи сезонної складової.

Оптимізація параметру згладжування

Необхідно обрати оптимальне значення $\alpha$ та $\ell_0$
Аналогічно до МНК, обираємо оптимальне за рахунок мінімізації суми квадтару відхилення: \[SSE = \sum_{t=1}^T(y_t - \hat{y}_{t|t-1})^2 = \sum_{t=1}^Te_t^2\]

ETS(A, N, N): модель SES

Компоненти:

Формула прогнозу: $\hat{y}_{t+h|t} = \ell_{t}$

Формула згладжування: $\ell_{t} = \alpha y_{t} + (1 - \alpha)\ell_{t-1}$

Залишки моделі: $e_t = y_t - \hat{y}_{t|t-1} = y_t - \ell_{t-1}$

Формула з залишками: $y_t = \ell_{t-1} + e_t; \quad \ell_{t}= \ell_{t-1}+\alpha(y_{t}-\ell_{t-1}) = \ell_{t-1}+\alpha e_{t}$

Похибки на навчальній вибірці призводять до коригування оцінки рівнів часового ряду в процесі згладжування.
Наприклад, якщо залишок в момент часу $t$ від’ємний, тобто $y_t < \hat{y}_{t|t-1}$, тоді рівень в момент часу $t-1$ був завищений. Новий рівень $\ell_t$ це попередній рівень $\ell_{t-1}$ скорегований на заниження.

ETS(A, N, N): специфікація моделі

ETS(y ~ error("A") + trend("N") + season("N"))

За замовчуванням підбираються оптимальні значення для $\alpha$ та $\ell_0$.

Або можна обрати вручну з trend()

trend("N", alpha = 0.5)
trend("N", alpha_range = c(0.2, 0.8))

Приклад: Експорт Алжиру

algeria_economy <- global_economy %>%
  filter(Country == "Algeria")
fit <- algeria_economy %>%
  model(ANN = ETS(Exports ~ error("A") + trend("N") + season("N")))
report(fit)

Series: Exports 
Model: ETS(A,N,N) 
  Smoothing parameters:
    alpha = 0.8399875 

  Initial states:
   l[0]
 39.539

  sigma^2:  35.6301

     AIC     AICc      BIC 
446.7154 447.1599 452.8968

Приклад: Експорт Алжиру

components(fit) %>% autoplot()

Приклад: Експорт Алжиру

components(fit) %>%
  left_join(fitted(fit), by = c("Country", ".model", "Year"))

# A dable: 59 x 7 [1Y]
# Key:     Country, .model [1]
# :        Exports = lag(level, 1) + remainder
   Country .model  Year Exports level remainder .fitted
   <fct>   <chr>  <dbl>   <dbl> <dbl>     <dbl>   <dbl>
 1 Algeria ANN     1959    NA    39.5    NA        NA  
 2 Algeria ANN     1960    39.0  39.1    -0.496    39.5
 3 Algeria ANN     1961    46.2  45.1     7.12     39.1
 4 Algeria ANN     1962    19.8  23.8   -25.3      45.1
 5 Algeria ANN     1963    24.7  24.6     0.841    23.8
 6 Algeria ANN     1964    25.1  25.0     0.534    24.6
 7 Algeria ANN     1965    22.6  23.0    -2.39     25.0
 8 Algeria ANN     1966    26.0  25.5     3.00     23.0
 9 Algeria ANN     1967    23.4  23.8    -2.07     25.5
10 Algeria ANN     1968    23.1  23.2    -0.630    23.8
# … with 49 more rows

Приклад: Експорт Алжиру

fit %>%
  forecast(h = 5) %>%
  autoplot(algeria_economy) +
  labs(y = "% від ВВП", title = "Експорт: Алжир")

Моделі з трендом: Хольт

Модель Хольта

Компоненти:

Прогноз: $\quad \hat{y}_{t+h|t} = \ell_{t} + hb_{t}$

Рівень: $\quad \quad\ell_{t} = \alpha y_{t} + (1 - \alpha)(\ell_{t-1} + b_{t-1})$

Тренд: $\quad \quad b_{t} = \beta^*(\ell_{t} - \ell_{t-1}) + (1 -\beta^*)b_{t-1},$

Параметри згладжування $\alpha$ та $\beta^*$ $\quad(0\le\alpha,\beta^*\le1)$
$\ell_t$ рівень: зважене середнє між $y_t$ та прогнозом на один крок вперед в момент часу $t$, $\quad(\ell_{t-1} + b_{t-1}=\hat{y}_{t|t-1})$
$b_t$ градієнт: зважене середнє між $(\ell_{t} - \ell_{t-1})$ та $b_{t-1}$, поточна та попередня оцінка нахилу тренду.

ETS(A,A,N)

Модель Хольта з адитивними залишками

Припустимо $\varepsilon_t=y_t-\ell_{t-1}-b_{t-1} \sim \text{NID}(0,\sigma^2)$
Тоді підставлючи похибки у рівняння: \[y_t =\ell_{t-1}+b_{t-1}+\varepsilon_t \\ \ell_t =\ell_{t-1}+b_{t-1}+\alpha \varepsilon_t \\ b_t =b_{t-1}+\alpha\beta^* \varepsilon_t\]
Для простоти запишемо $\beta=\alpha \beta^*$, тоді: \[b_t =b_{t-1}+\beta \varepsilon_t\]

Еспоненціальне згладжування: тренд

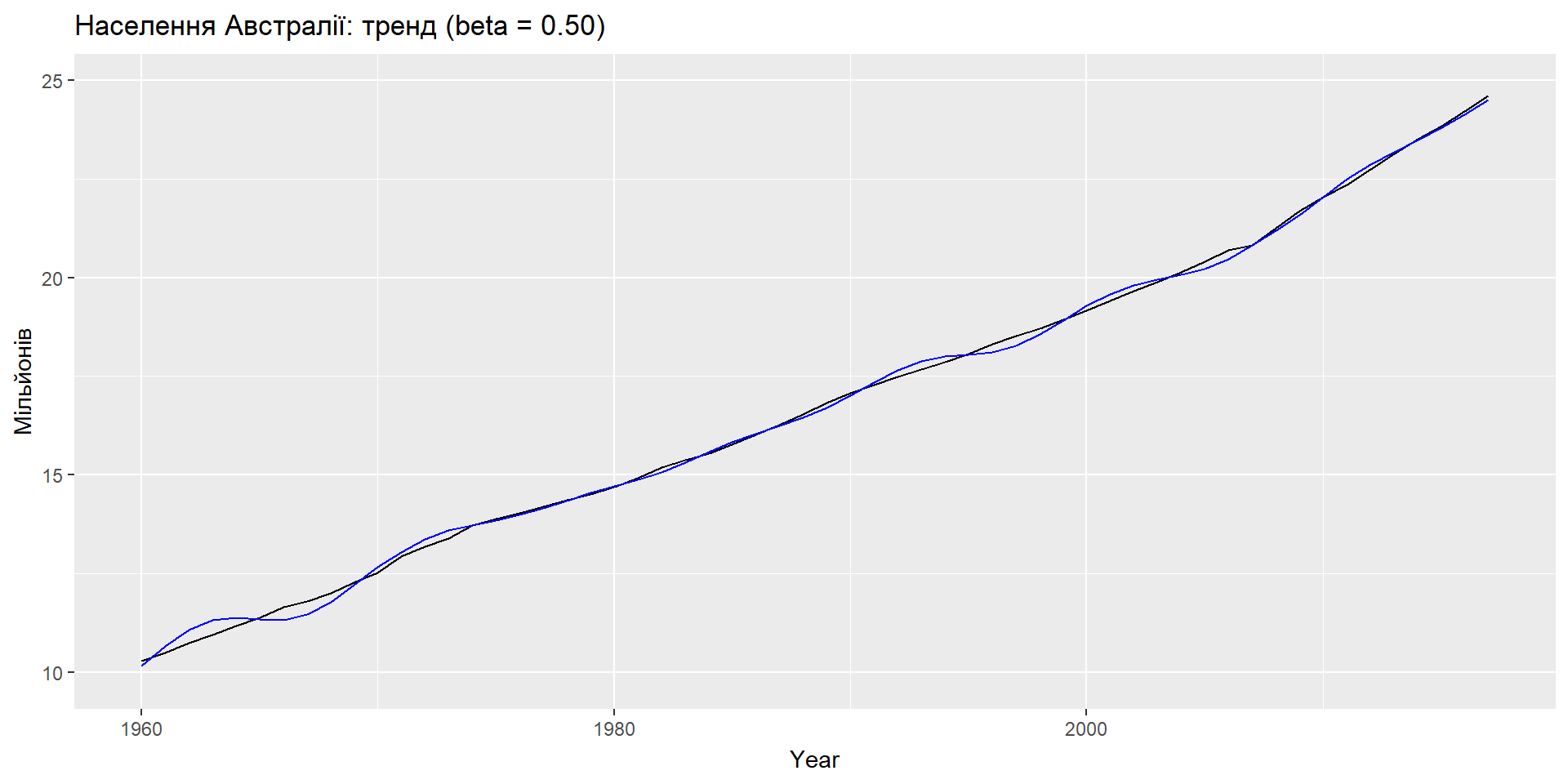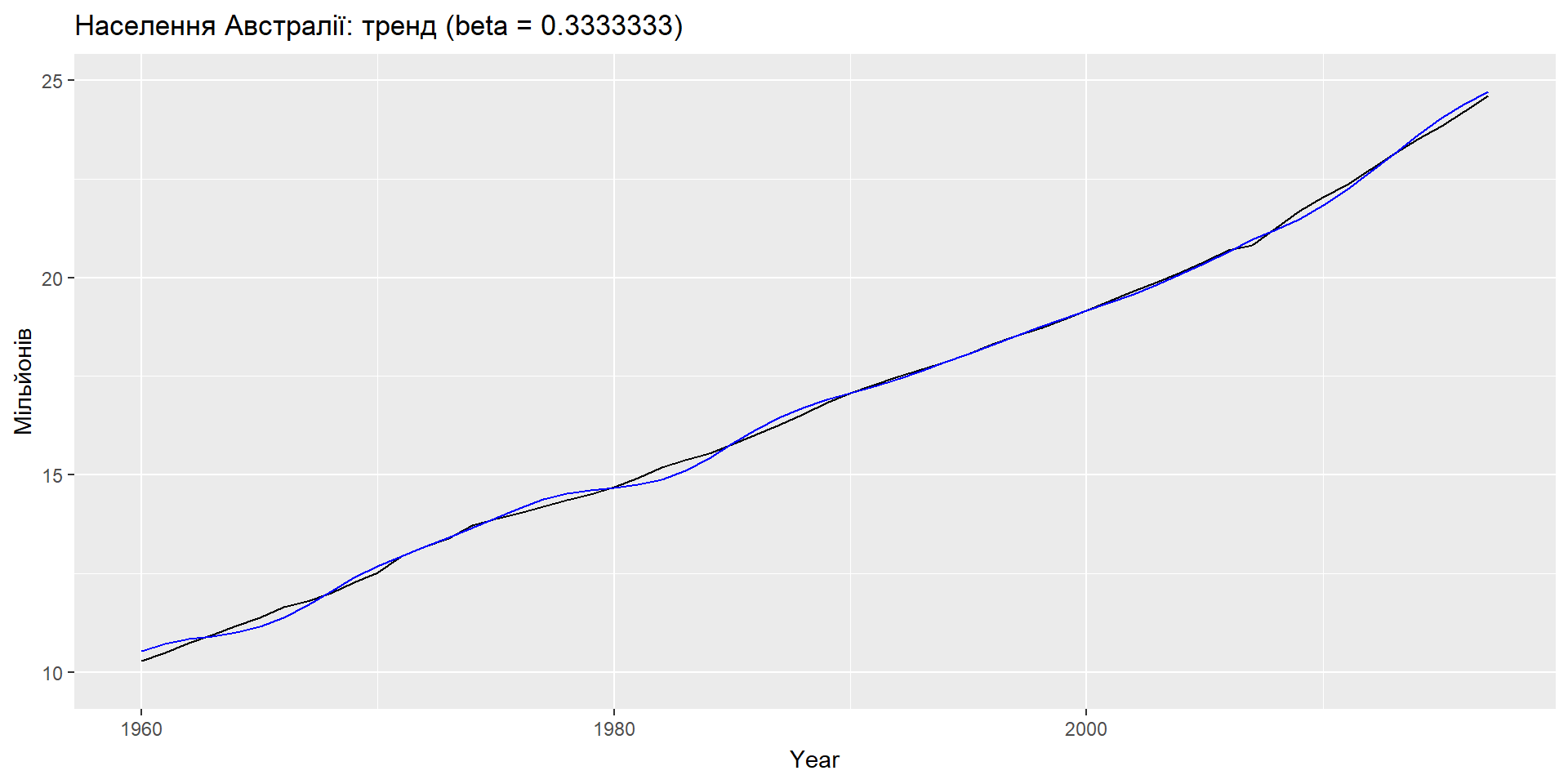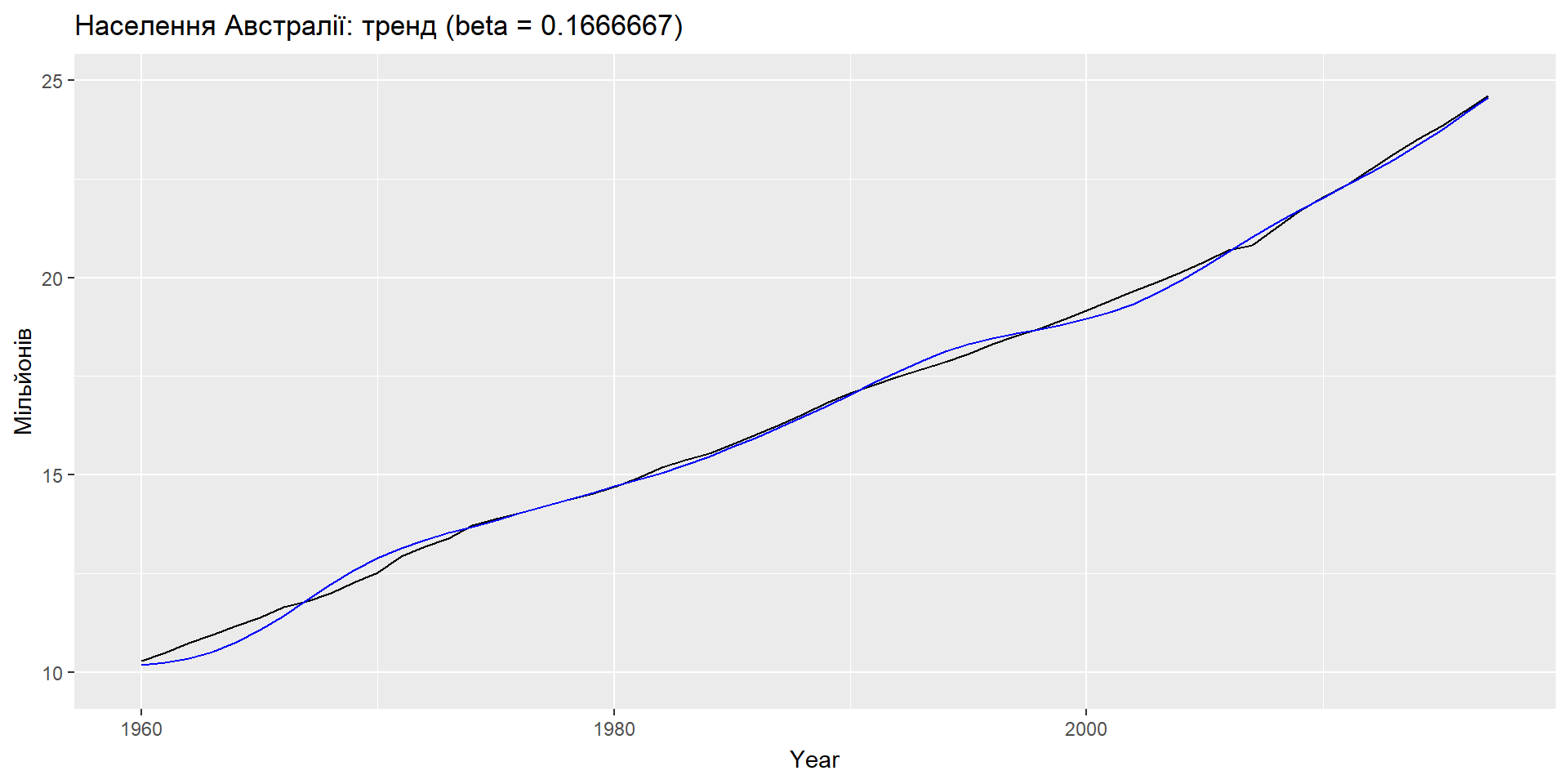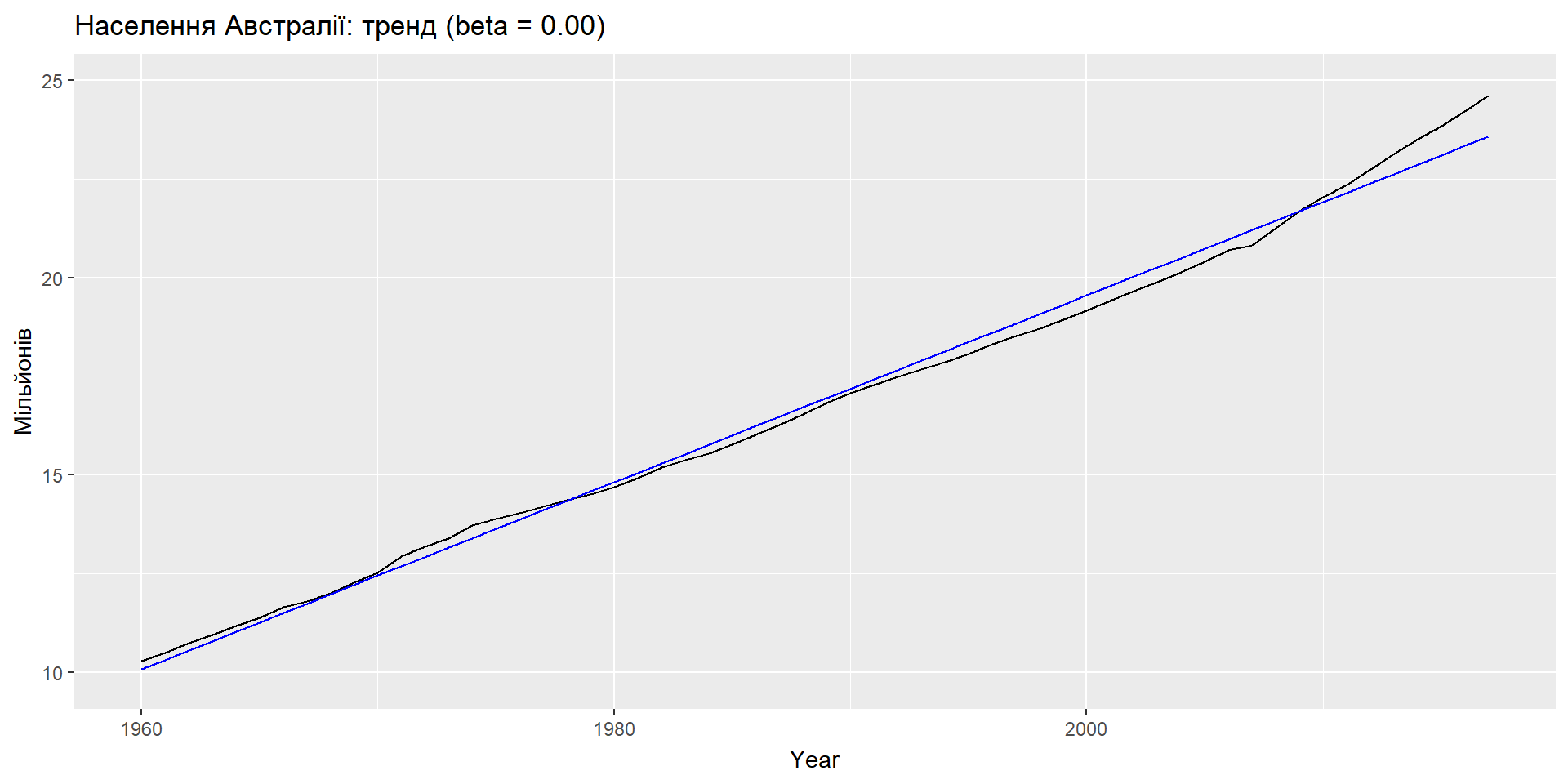
ETS(A,A,N): специфікація моделі

ETS(y ~ error("A") + trend("A") + season("N"))

За замовчуванням підбираються оптимальні значення для $\beta$ та $b_0$.

$\beta$ можна обрати вручну з trend()

trend("A", beta = 0.004)
trend("A", beta_range = c(0, 0.1))

Приклад: населення Австралії

aus_economy <- global_economy %>% filter(Code == "AUS") %>%
  mutate(Pop = Population/1e6)
fit <- aus_economy %>%
  model(AAN = ETS(Pop ~ error("A") + trend("A") + season("N")))
report(fit)

Series: Pop 
Model: ETS(A,A,N) 
  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.3266366 

  Initial states:
     l[0]      b[0]
 10.05414 0.2224818

  sigma^2:  0.0041

      AIC      AICc       BIC 
-76.98569 -75.83184 -66.68347

Приклад: населення Австралії

components(fit) %>%
  left_join(fitted(fit), by = c("Country", ".model", "Year"))

# A dable: 59 x 8 [1Y]
# Key:     Country, .model [1]
# :        Pop = lag(level, 1) + lag(slope, 1) + remainder
   Country   .model  Year   Pop level slope remainder .fitted
   <fct>     <chr>  <dbl> <dbl> <dbl> <dbl>     <dbl>   <dbl>
 1 Australia AAN     1959  NA    10.1 0.222 NA           NA  
 2 Australia AAN     1960  10.3  10.3 0.222 -0.000145    10.3
 3 Australia AAN     1961  10.5  10.5 0.217 -0.0159      10.5
 4 Australia AAN     1962  10.7  10.7 0.231  0.0418      10.7
 5 Australia AAN     1963  11.0  11.0 0.223 -0.0229      11.0
 6 Australia AAN     1964  11.2  11.2 0.221 -0.00641     11.2
 7 Australia AAN     1965  11.4  11.4 0.221 -0.000314    11.4
 8 Australia AAN     1966  11.7  11.7 0.235  0.0418      11.6
 9 Australia AAN     1967  11.8  11.8 0.206 -0.0869      11.9
10 Australia AAN     1968  12.0  12.0 0.208  0.00350     12.0
# … with 49 more rows

Приклад: населення Австралії

fit %>%
  forecast(h = 10) %>%
  autoplot(aus_economy) +
  labs(y = "Мільйонів", title= "населення: Австралія")

Метод демпфованого тренду

Компоненти:

\[\hat{y}_{t+h|t} = \ell_{t} + (\phi+\phi^2 + \dots + \phi^{h})b_{t} \\ \ell_{t} = \alpha y_{t} + (1 - \alpha)(\ell_{t-1} + \phi b_{t-1}) \\ b_{t} = \beta^*(\ell_{t} - \ell_{t-1}) + (1 -\beta^*)\phi b_{t-1}\]

Параметр демпфування $0<\phi<1$
Коли $\phi=1$, модель ідентична моделі Хольта
Якщо $h\rightarrow\infty$, $\hat{y}_{T+h|T}\rightarrow \ell_T+\frac{\phi b_T}{(1-\phi)}$
Короткострокові прогнози мають тренд, довгострокові прогнози - незмінні.

Приклад: населення Австралії

aus_economy %>%
  model(holt = ETS(Pop ~ error("A") + trend("Ad") + season("N"))) %>%
  forecast(h = 20) %>%
  autoplot(aus_economy)

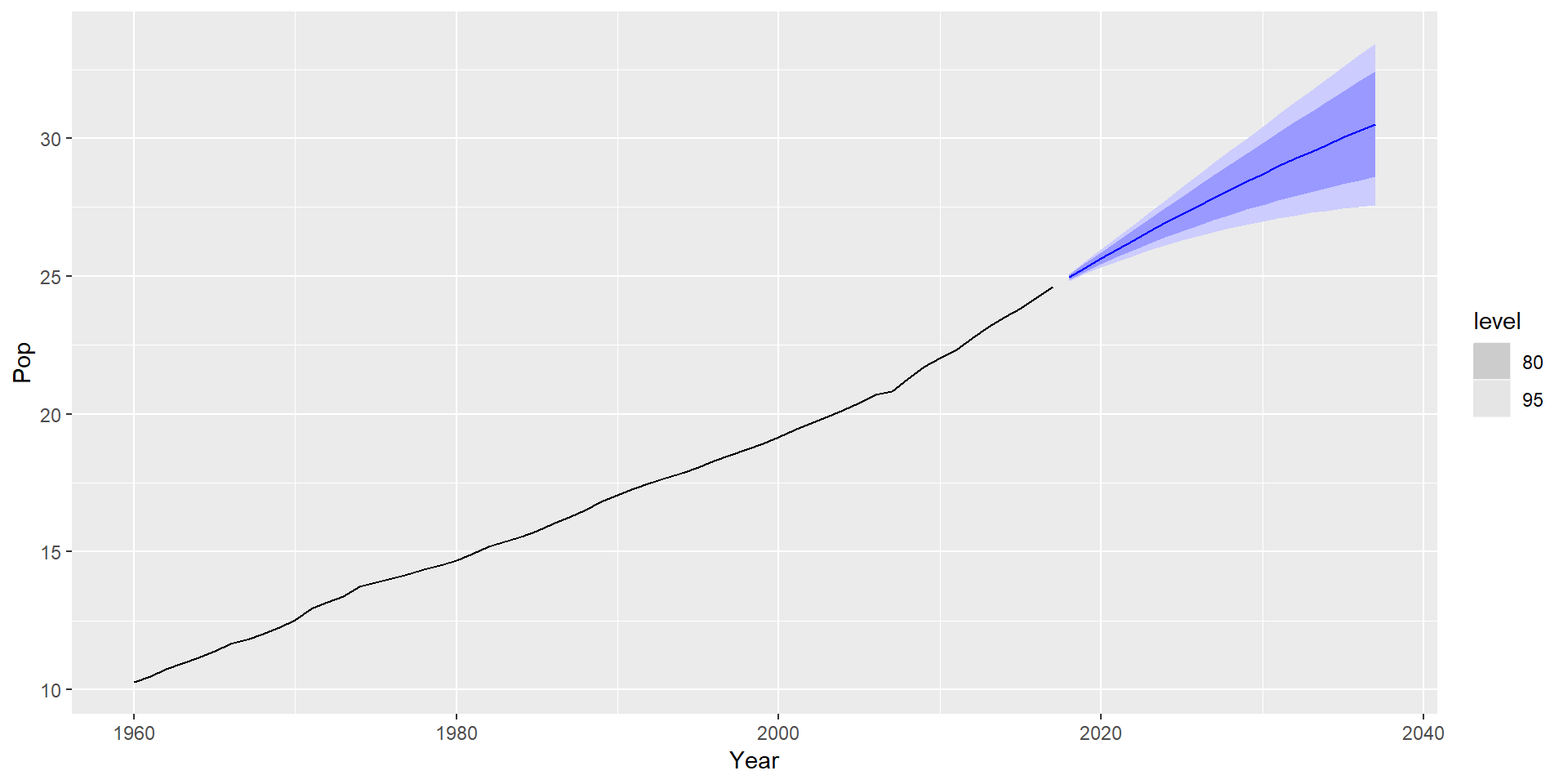
Приклад: населення Австралії

fit <- aus_economy %>%
  filter(Year <= 2010) %>%
  model(
    ses = ETS(Pop ~ error("A") + trend("N") + season("N")),
    holt = ETS(Pop ~ error("A") + trend("A") + season("N")),
    damped = ETS(Pop ~ error("A") + trend("Ad") + season("N"))
  )

tidy(fit)
accuracy(fit)

Приклад: населення Австралії

term	SES	Linear trend	Damped trend
$\alpha$	1.00	1.00	1.00
$\beta^*$		0.30	0.40
$\phi$			0.98
$\ell_0$	10.28	10.05	10.04
$b_0$		0.22	0.25
Training RMSE	0.24	0.06	0.07
Test RMSE	1.63	0.15	0.21
Test MASE	6.18	0.55	0.75
Test MAPE	6.09	0.55	0.74
Test MAE	1.45	0.13	0.18

Моделі з сезонністю: Хольт-Вінтерс

Адитивна модель Хольта-Вінтерса

Холь та Вінтерс розширили модель Хольта, яка включає сезонність.

Компоненти:

\[\hat{y}_{t+h|t} = \ell_{t} + hb _{t} + s_{t+h-m(k+1)}\] \[\ell_{t} = \alpha(y_{t} - s_{t-m}) + (1 - \alpha)(\ell_{t-1} + b_{t-1})\] \[b_{t} = \beta^*(\ell_{t} - \ell_{t-1}) + (1 - \beta^*)b_{t-1}\] \[s_{t} = \gamma (y_{t}-\ell_{t-1}-b_{t-1}) + (1-\gamma)s_{t-m}\]

$k=$ ціла частина від $(h-1)/m$. Використовує останній сезон для прогнозування.
Параметри: $0\le \alpha\le 1$, $0\le \beta^*\le 1$, $0\le \gamma\le 1-\alpha$ та $m=$ період сезонності.

Адитивна модель Хольта-Вінтерса

Сезонна складова зазвичай записується як \[s_{t} = \gamma^*(y_{t}-\ell_{t})+(1-\gamma^*)s_{t-m}\]
Замінивши $\ell_t$: \[s_{t} = \gamma^*(1-\alpha) (y_{t}-\ell_{t-1}-b_{t-1})+ [1-\gamma^*(1-\alpha)]s_{t-m}\]
Записуємо \[\gamma=\gamma^*(1-\alpha)\]
Звичайне обмеження параметру $0\le\gamma^*\le1$ переписується як \[0\le\gamma\le(1-\alpha)\]

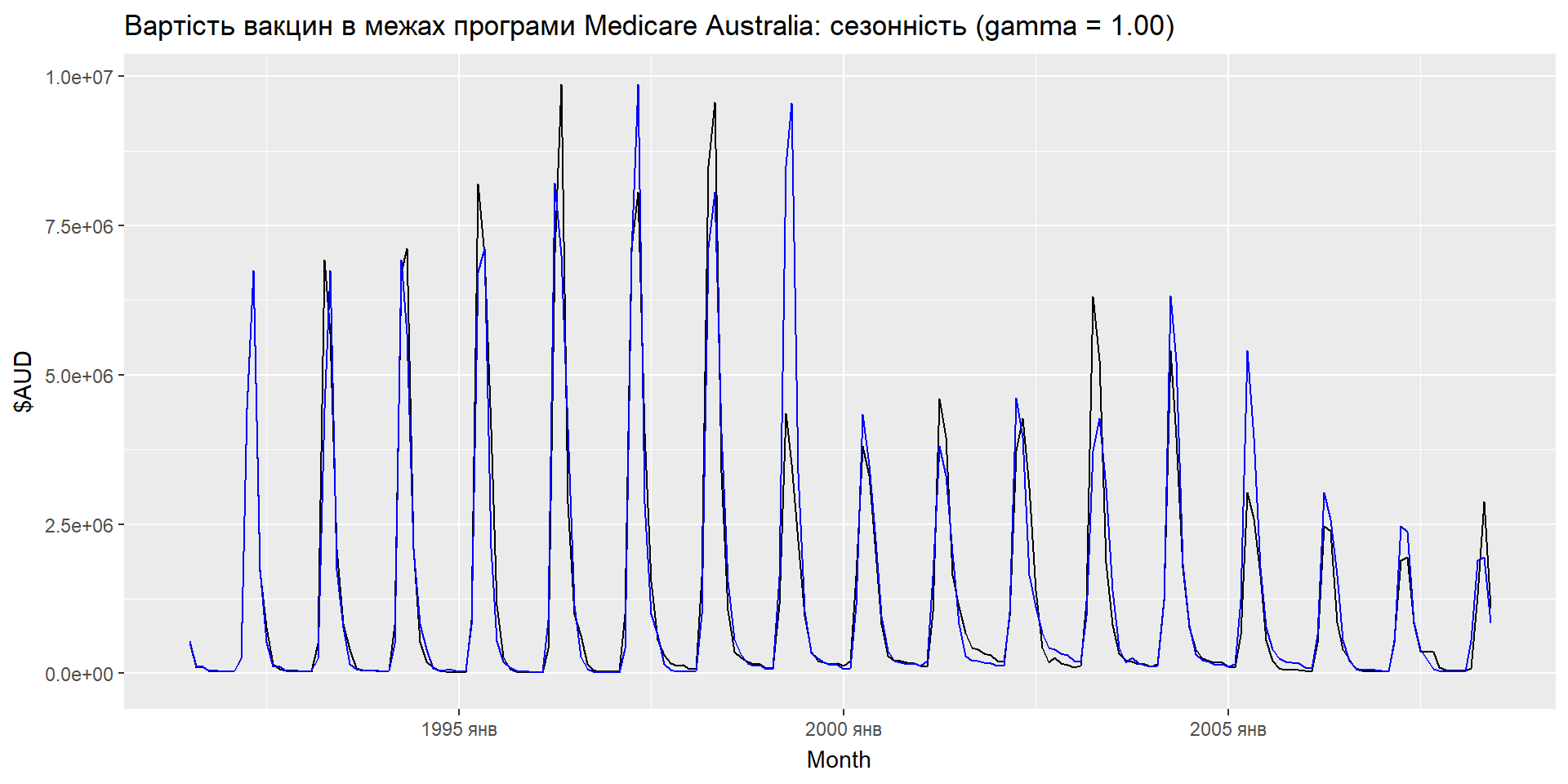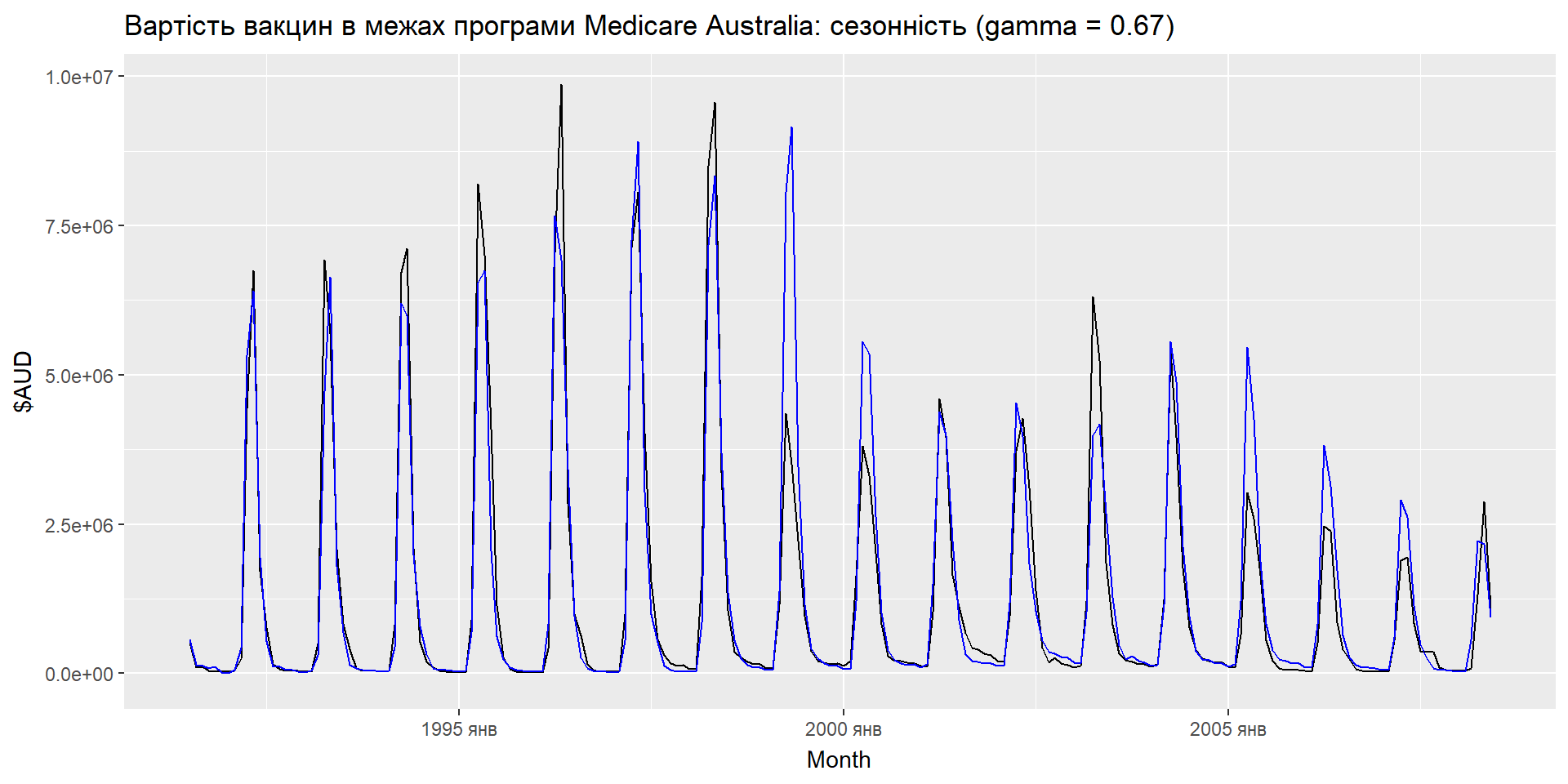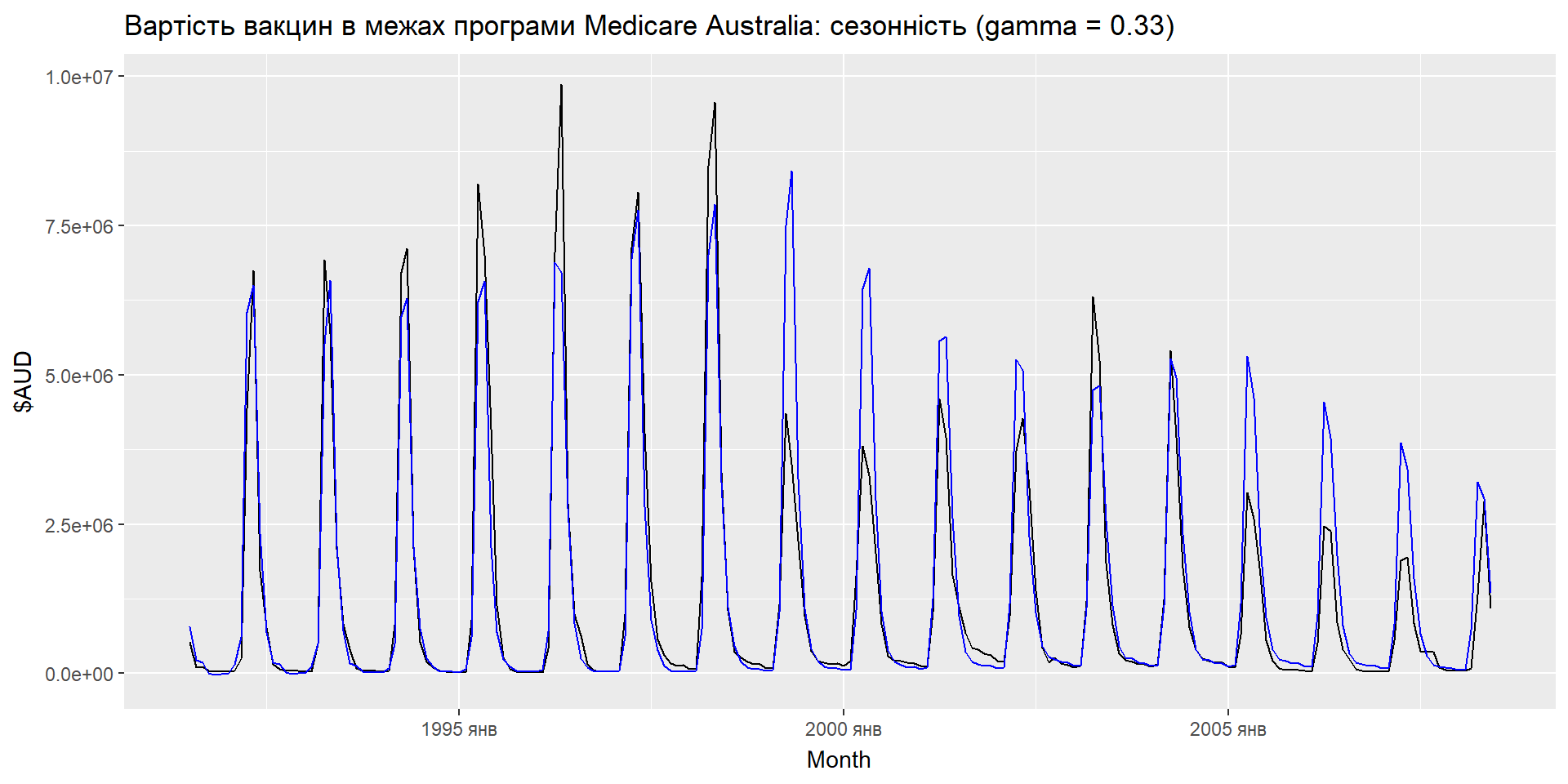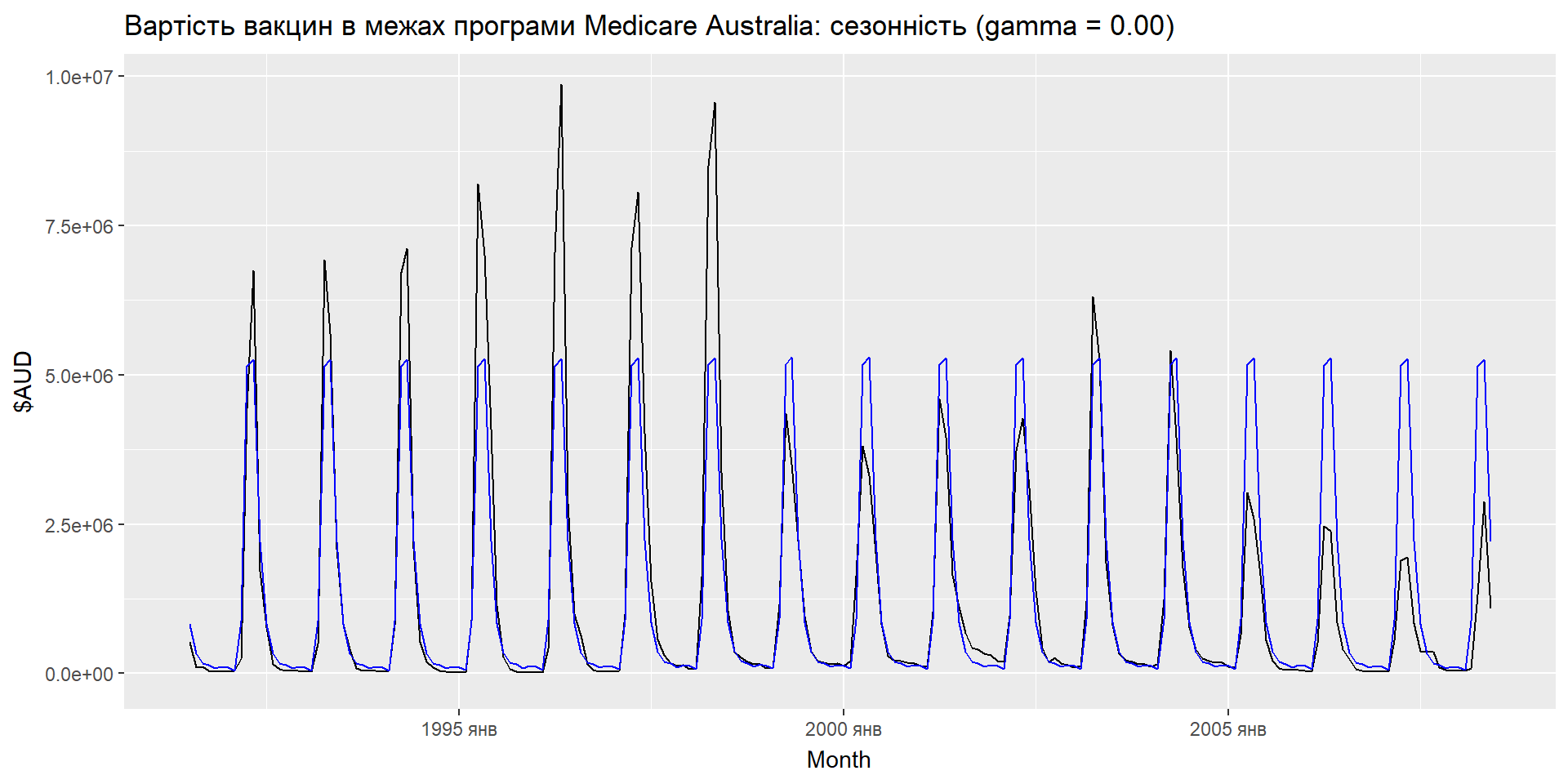
Еспоненціальне згладжування: сезонність

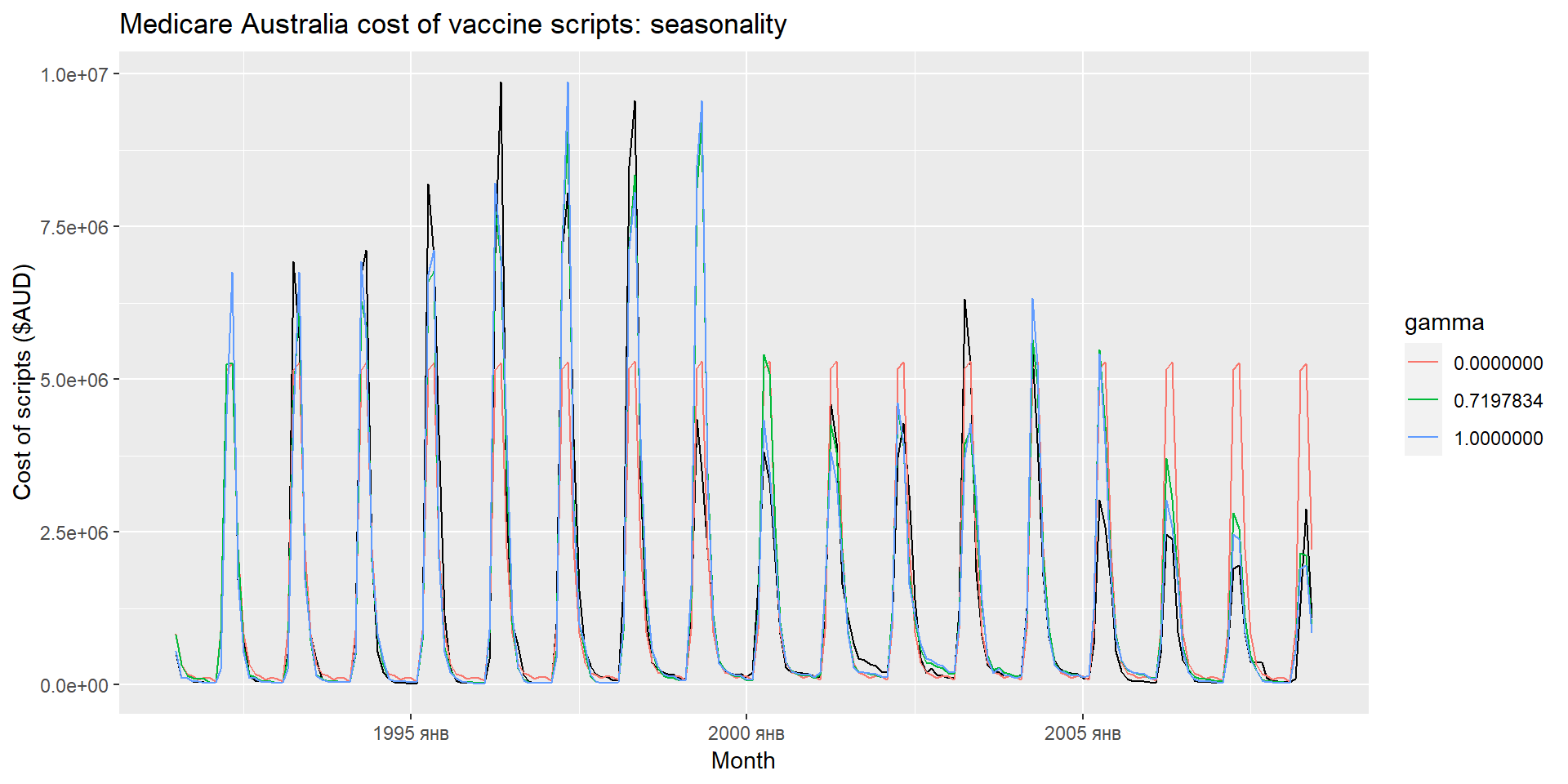
ETS(A,A,A)

Адитивна модель Хольта-Вінтерса з адитивними залишками

Рівняння прогнозу: $\quad\quad\hat{y}_{t+h|t} = \ell_{t} + hb_{t} + s_{t+h-m(k+1)}$

Рівняння спостережень: $\quad y_t=\ell_{t-1}+b_{t-1}+s_{t-m} + \varepsilon_t$

Рівняння компонент: $\quad\quad\quad\ell_t=\ell_{t-1}+b_{t-1}+\alpha \varepsilon_t$ \[b_t=b_{t-1}+\beta \varepsilon_t \\ s_t = s_{t-m} + \gamma\varepsilon_t\]

Похибки прогнозу: $\varepsilon_{t} = y_t - \hat{y}_{t|t-1}$
$k$ ціла частина з $(h-1)/m$

Мультиплікативний метод Хольта-Вінтерса

Коли сезонні коливання змінюються пропорційно зміні рівнів ряду.

Компоненти: \[\hat{y}_{t+h|t} = (\ell_{t} + hb_{t})s_{t+h-m(k+1)} \\ \quad\quad\ell_{t} = \alpha \frac{y_{t}}{s_{t-m}} + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \\ \quad b_{t} = \beta^*(\ell_{t}-\ell_{t-1}) + (1 - \beta^*)b_{t-1} \\ \quad\quad s_{t} = \gamma \frac{y_{t}}{(\ell_{t-1} + b_{t-1})} + (1 - \gamma)s_{t-m}\]

$k$ ціла частина з $(h-1)/m$
Для адитивного методу $s_t$ у абсолютних значеннях: $\sum_i s_i \approx 0$
Для мультиплікативного методу $s_t$ у відносних значеннях: $\sum_i s_i \approx m$

ETS(M,A,M)

Мультиплікативний метод Хольта-Вінтерса з мультиплікативними залишками

Рівняння прогнозу: $\quad\quad\quad\hat{y}_{t+h|t} = (\ell_{t} + hb_{t}) s_{t+h-m(k+1)}$

Рівняння спостережень: $\quad y_t = (\ell_{t-1}+b_{t-1})s_{t-m}(1 + \varepsilon_t)$

Рівняння компонент: $\quad\quad\ell_t=(\ell_{t-1}+b_{t-1})(1+\alpha \varepsilon_t)$ \[\quad \quad b_t=b_{t-1} +\beta(\ell_{t-1}+b_{t-1}) \varepsilon_t \\ s_t = s_{t-m}(1 + \gamma\varepsilon_t)\]

Похибки прогнозу: $\varepsilon_{t} = (y_t - \hat{y}_{t|t-1})/\hat{y}_{t|t-1}$
$k$ ціла частина з $(h-1)/m$

Приклад: туризм Австралії

aus_holidays <- tourism %>%
  filter(Purpose == "Holiday") %>%
  summarise(Trips = sum(Trips))
fit <- aus_holidays %>%
  model(
    additive = ETS(Trips ~ error("A") + trend("A") + season("A")),
    multiplicative = ETS(Trips ~ error("M") + trend("A") + season("M"))
  )
fc <- fit %>% forecast()

Приклад: туризм Австралії

fc %>%
  autoplot(aus_holidays, level = NULL) +
  labs(y = "Тисяч", title = "Нічні поїздки")

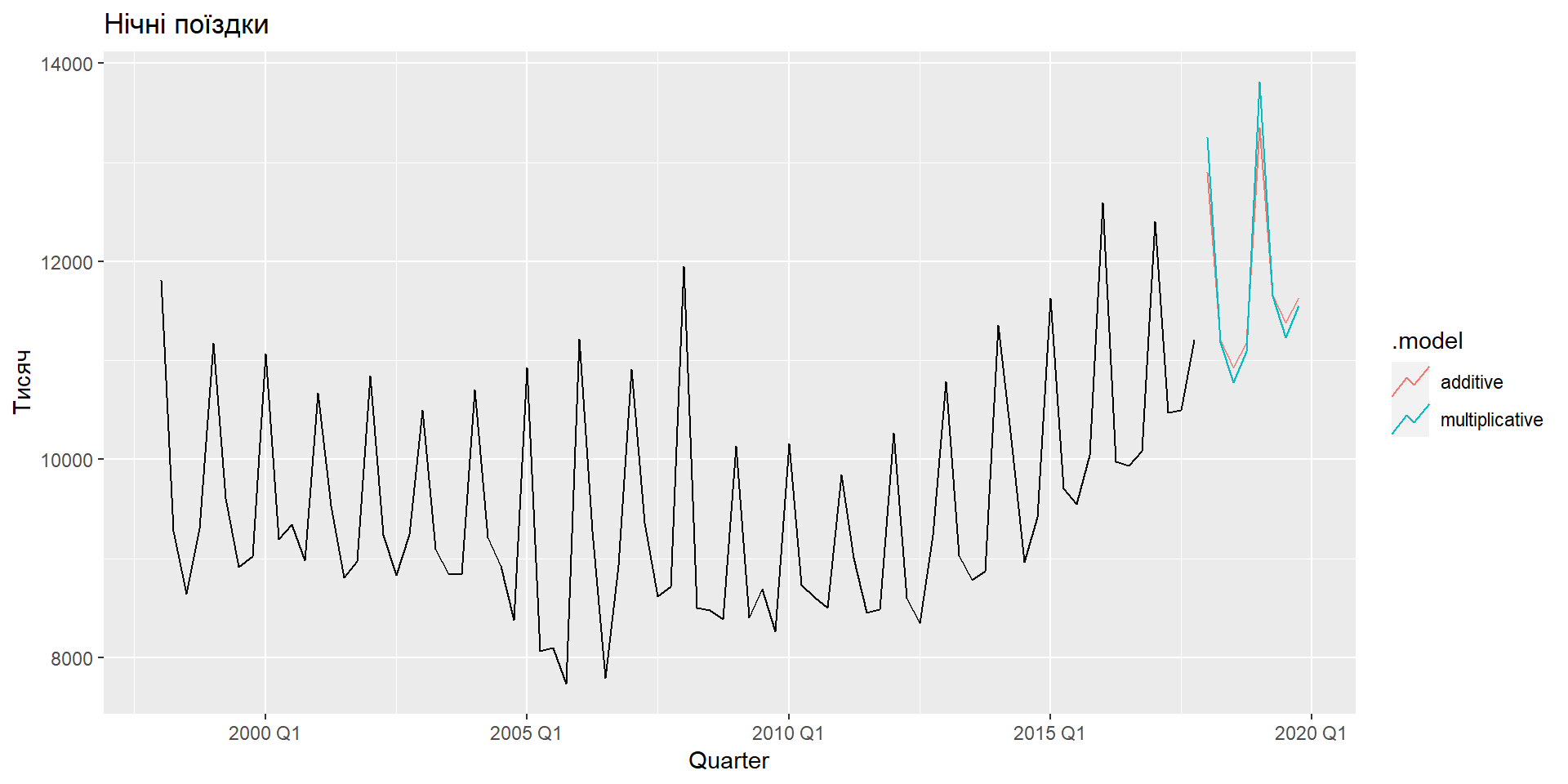
Компоненти

components(fit)

# A dable: 168 x 7 [1Q]
# Key:     .model [2]
# :        Trips = lag(level, 1) + lag(slope, 1) + lag(season, 4) + remainder
   .model   Quarter  Trips level slope season remainder
   <chr>      <qtr>  <dbl> <dbl> <dbl>  <dbl>     <dbl>
 1 additive 1997 Q1    NA    NA   NA    1512.      NA  
 2 additive 1997 Q2    NA    NA   NA    -290.      NA  
 3 additive 1997 Q3    NA    NA   NA    -684.      NA  
 4 additive 1997 Q4    NA  9899. -37.4  -538.      NA  
 5 additive 1998 Q1 11806. 9964. -24.5  1512.     433. 
 6 additive 1998 Q2  9276. 9851. -35.6  -290.    -374. 
 7 additive 1998 Q3  8642. 9700. -50.2  -684.    -489. 
 8 additive 1998 Q4  9300. 9694. -44.6  -538.     188. 
 9 additive 1999 Q1 11172. 9652. -44.3  1512.      10.7
10 additive 1999 Q2  9608. 9676. -35.6  -290.     290. 
# … with 158 more rows

Компоненти

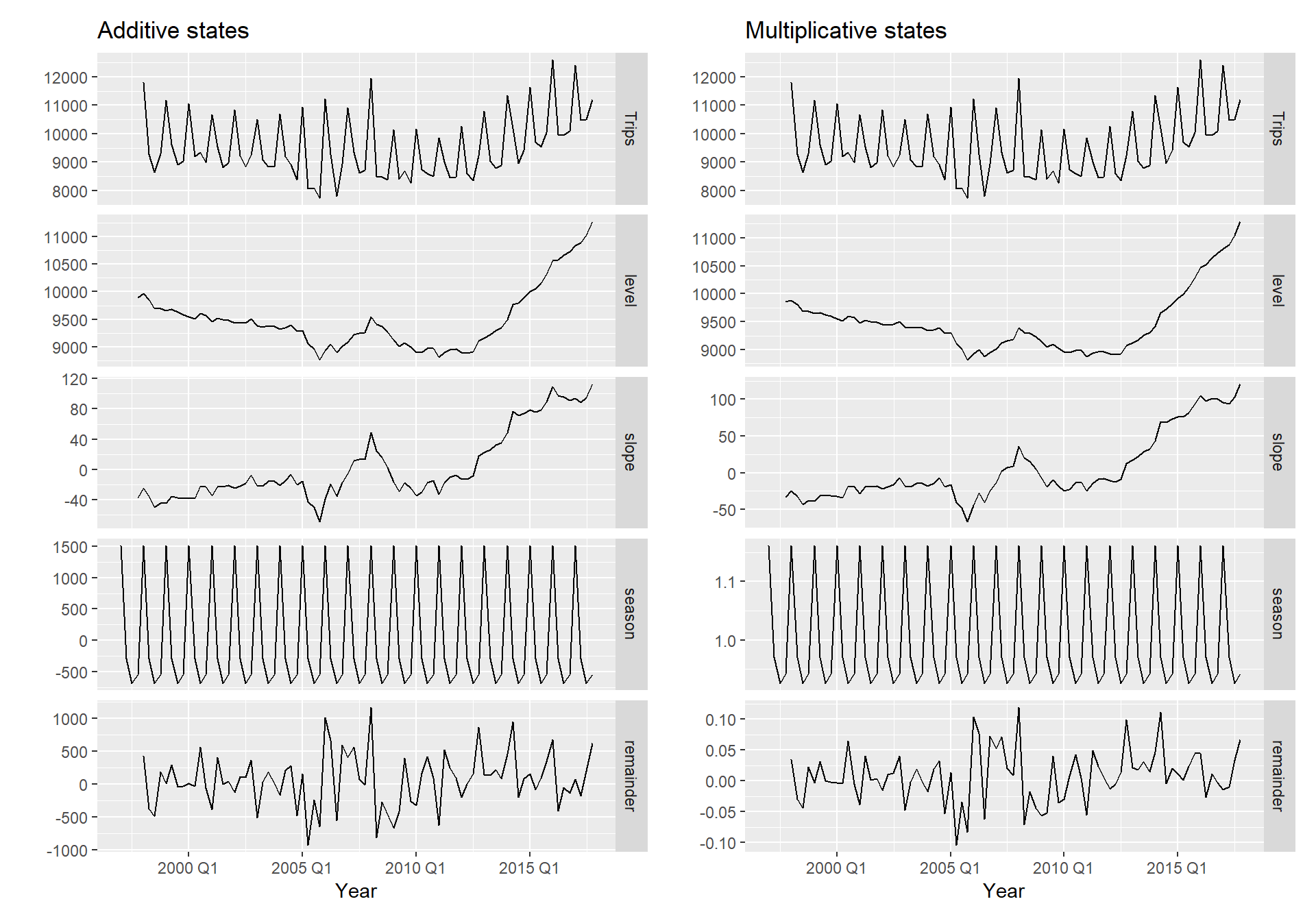
Демпфований метод Хольта-Вінтерса

Часто єдиний найточніший метод прогнозування для сезонних даних:

\[\hat{y}_{t+h|t} = [\ell_{t} + (\phi+\phi^2 + \dots + \phi^{h})b_{t}]s_{t+h-m(k+1)} \\ \ell_{t} = \alpha(y_{t} / s_{t-m}) + (1 - \alpha)(\ell_{t-1} + \phi b_{t-1})\\ b_{t} = \beta^*(\ell_{t} - \ell_{t-1}) + (1 - \beta^*)\phi b_{t-1} \\ s_{t} = \gamma \frac{y_{t}}{(\ell_{t-1} + \phi b_{t-1})} + (1 - \gamma)s_{t-m}\]

Хольт-Вінтерс для щоденних даних

 sth_cross_ped <- pedestrian %>%
  filter(Date >= "2016-07-01",
         Sensor == "Southern Cross Station") %>%
  index_by(Date) %>%
  summarise(Count = sum(Count)/1000)

sth_cross_ped %>%
  filter(Date <= "2016-07-31") %>%
  model(
    hw = ETS(Count ~ error("M") + trend("Ad") + season("M"))
  ) %>%
  forecast(h = "2 weeks") %>%
  autoplot(sth_cross_ped %>% filter(Date <= "2016-08-14")) +
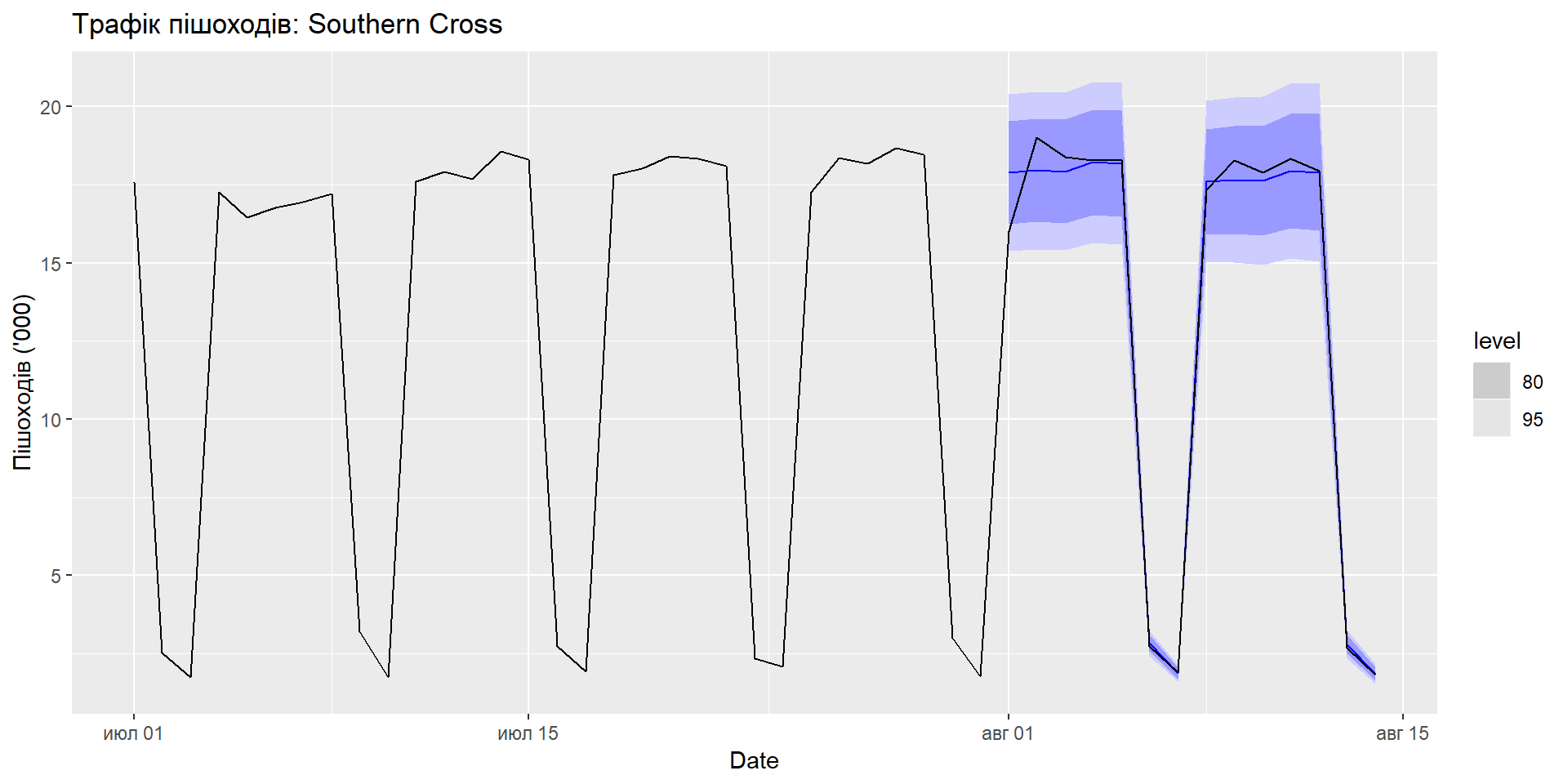
  labs(title = "Трафік пішоходів: Southern Cross",
       y="Пішоходів ('000)")

Хольт-Вінтерс для щоденних даних

Інноваційні моделі

Методи експоненціального згладжування

	Компонента сезонності
Компонента тренду	N (Відсутня)	A (Адитивна)	M (Мультиплікативна)
N (Відсутня)	(N,N)	(N,A)	(N,M)
A (Адитивний)	(A,N)	(A,A)	(A,M)
Ad (Адитивний демпфований)	(Ad, N)	(Ad, A)	(Ad, M)

$(N,N)$: Просте експоненціальне згаджування
$(A,N)$:    Лінійний метод Хольта
$(A_d,N)$: Адитивний демпфований тред
$(A,A)$:     Адитивний метод Хольта-Вінтерса
$(A,M)$:    Мультиплікативний метод Хольта-Вінтерса
$(A_d,M)$: Демпфований мультиплікативний метод Хольта-Вінтерса

ETS моделі

АДИТИВНІ ЗАЛИШКИ
	Компонента сезонності
Компонента тренду	N (Відсутня)	A (Адитивна)	M (Мультиплікативна)
N (Відсутня)	(A,N,N)	(A,N,A)	(A,N,M)
A (Адитивний)	(A,A,N)	(A,A,A)	(A,A,M)
Ad (Адитивний демпфований)	(A,Ad,N)	(A,Ad,A)	(A,Ad,M)

ETS моделі

МУЛЬТИПЛІКАТИВНІ ЗАЛИШКИ
	Компонента сезонності
Компонента тренду	N (Відсутня)	A (Адитивна)	M (Мультиплікативна)
N (Відсутня)	(M,N,N)	(M,N,A)	(M,N,M)
A (Адитивний)	(M,A,N)	(M,A,A)	(M,A,M)
Ad (Адитивний демпфований)	(M,Ad,N)	(M,Ad,A)	(M,Ad,M)

Моделі з адитивними залишками

Моделі з мультиплікативними залишками

Оцінювання ETS моделей

Параметри згладжування $\alpha$, $\beta$, $\gamma$ та $\phi$, а також початкові значення $\ell_0$, $b_0$, $s_0,s_{-1},\dots,s_{ -m+1}$ оцінюються шляхом максимізації “правдоподібності” = ймовірності даних, що випливають із зазначеної моделі.
Для моделей з адитивними помилками підхід еквівалентний мінімізації SSE.
Для моделей з мультиплікативними помилками підхід НЕ еквівалентний мінімізації SSE.

Оцінювання ETS моделей

Традиційно: * $0< \alpha,\beta^*,\gamma^*,\phi<1$ * У модель ми підставляємо $\beta=\alpha\beta^*$ та $\gamma=(1-\alpha)\gamma^*$ * Тому $0< \alpha <1$, $0 < \beta < \alpha$ та $0< \gamma < 1-\alpha$ * $0.8<\phi<0.98$ - для полегшення розрахунку

Допустимі обмеження: * Щоб запобігти впливу спостережень з далекого минулого на поточні прогнози. * Зазвичай (але не завжди) менші обмежування ніж в традиційному підході. * Наприклад, для ETS(A,N,N):
традиційно $0< \alpha <1$ припускається $0< \alpha <2$.

Вибір моделі

Інформаційний критерій Акаіке (AIC)

\[\text{AIC} = -2\log(\text{L}) + 2k\] де $L$ – правдоподібність, а $k$ – кількість параметрів моделі.

Скорегований AICc

\[\text{AIC}_{\text{c}} = \text{AIC} + \frac{2k(k+1)}{T-k-1}\] для корегування зміщення.

Баесовий інформаційний криетрій (BIC)

\[\text{BIC} = \text{AIC} + k[\log(T)-2].\]

Автоматизація прогнозування:

З роботи Hyndman та інших (IJF, 2002):

Застосовується кожна модель, яка відповідає даним.
Оптимізуються параметри та початкові значення за допомогою ММП (або іншого критерію).
Обирається найкращий метод за допомогою AICc:
Будується прогноз, використовуючи найкращий метод.
Обчислюються довірчі інтервали.

Метод дуже добре показав себе на змаганнях М3.

Приклад: населення країн світу

fit <- global_economy %>%
  mutate(Pop = Population / 1e6) %>%
  model(ets = ETS(Pop))

fit

# A mable: 263 x 2
# Key:     Country [263]
   Country                      ets
   <fct>                    <model>
 1 Afghanistan         <ETS(A,A,N)>
 2 Albania             <ETS(M,A,N)>
 3 Algeria             <ETS(M,A,N)>
 4 American Samoa      <ETS(M,A,N)>
 5 Andorra             <ETS(M,A,N)>
 6 Angola              <ETS(M,A,N)>
 7 Antigua and Barbuda <ETS(M,A,N)>
 8 Arab World          <ETS(M,A,N)>
 9 Argentina           <ETS(A,A,N)>
10 Armenia             <ETS(M,A,N)>
# … with 253 more rows

Приклад: населення країн світу

fit %>%
  forecast(h = 5)

# A fable: 1,315 x 5 [1Y]
# Key:     Country, .model [263]
   Country     .model  Year             Pop .mean
   <fct>       <chr>  <dbl>          <dist> <dbl>
 1 Afghanistan ets     2018    N(36, 0.012) 36.4 
 2 Afghanistan ets     2019    N(37, 0.059) 37.3 
 3 Afghanistan ets     2020     N(38, 0.16) 38.2 
 4 Afghanistan ets     2021     N(39, 0.35) 39.0 
 5 Afghanistan ets     2022     N(40, 0.64) 39.9 
 6 Albania     ets     2018 N(2.9, 0.00012)  2.87
 7 Albania     ets     2019   N(2.9, 6e-04)  2.87
 8 Albania     ets     2020  N(2.9, 0.0017)  2.87
 9 Albania     ets     2021  N(2.9, 0.0036)  2.86
10 Albania     ets     2022  N(2.9, 0.0066)  2.86
# … with 1,305 more rows

Приклад: електроенергія України

energy <- vroom("https://git.io/JDYAX") %>%
  pivot_longer(!time, names_to = "type", values_to = "value") %>%
   mutate(time = ymd_hms(time)) %>%
   as_tsibble(index = time, key = type)

energy

# A tsibble: 750,541 x 3 [1h] <UTC>
# Key:       type [11]
   time                type  value
   <dttm>              <chr> <dbl>
 1 2014-01-01 00:00:00 AES   10728
 2 2014-01-01 01:00:00 AES   10606
 3 2014-01-01 02:00:00 AES   10515
 4 2014-01-01 03:00:00 AES   10475
 5 2014-01-01 04:00:00 AES   10427
 6 2014-01-01 05:00:00 AES   10473
 7 2014-01-01 06:00:00 AES   10469
 8 2014-01-01 07:00:00 AES   10493
 9 2014-01-01 08:00:00 AES   10479
10 2014-01-01 09:00:00 AES   10455
# … with 750,531 more rows

Приклад: електроенергія України

energy_fit <- energy %>%
  model(ets = ETS(value))

energy_fit

# A mable: 11 x 2
# Key:     type [11]
   type                  ets
   <chr>             <model>
 1 AES         <ETS(A,Ad,N)>
 2 CONSUMPTION  <ETS(M,N,M)>
 3 GAES_GEN     <ETS(A,N,A)>
 4 GAES_PUMP    <ETS(A,N,A)>
 5 GES          <ETS(A,N,A)>
 6 TEC         <ETS(M,Ad,M)>
 7 TES          <ETS(M,N,M)>
 8 UK_BLR_RUS   <ETS(A,N,A)>
 9 UK_EURO      <ETS(A,N,A)>
10 UK_MLD       <ETS(A,N,A)>
11 VDE         <ETS(A,Ad,A)>

Приклад: електроенергія України

energy_fit %>%
  filter(type == "VDE") %>%
  report()

Series: value 
Model: ETS(A,Ad,A) 
  Smoothing parameters:
    alpha = 0.8048643 
    beta  = 0.0001001706 
    gamma = 0.1951258 
    phi   = 0.9751766 

  Initial states:
     l[0]      b[0]      s[0]     s[-1]     s[-2]    s[-3]    s[-4]   s[-5]
 124.8749 0.4850034 -205.5111 -207.4407 -207.1193 -204.368 -185.616 -123.64
     s[-6]    s[-7]    s[-8]    s[-9]   s[-10]   s[-11]   s[-12]   s[-13]
 -18.78656 107.8249 234.3663 349.6245 423.2788 462.4296 449.4224 369.3013
   s[-14]   s[-15]    s[-16]    s[-17]    s[-18]    s[-19]    s[-20]   s[-21]
 230.1887 46.91798 -102.0972 -180.2585 -201.2115 -208.0023 -208.1248 -207.123
    s[-22]   s[-23]
 -206.8092 -207.246

  sigma^2:  8130.499

    AIC    AICc     BIC 
1373796 1373796 1374070

Приклад: електроенергія України

energy_fit %>%
  filter(type == "VDE") %>%
  components(energy_fit)

# A dable: 68,255 x 8 [1h] <UTC>
# Key:     type, .model [1]
# :        value = lag(level, 1) + 0.975176649672342 * lag(slope, 1) +
#   lag(season, 24) + remainder
   type  .model time                value level slope season remainder
   <chr> <chr>  <dttm>              <dbl> <dbl> <dbl>  <dbl>     <dbl>
 1 VDE   ets    2013-12-31 00:00:00    NA    NA    NA -207.         NA
 2 VDE   ets    2013-12-31 01:00:00    NA    NA    NA -207.         NA
 3 VDE   ets    2013-12-31 02:00:00    NA    NA    NA -207.         NA
 4 VDE   ets    2013-12-31 03:00:00    NA    NA    NA -208.         NA
 5 VDE   ets    2013-12-31 04:00:00    NA    NA    NA -208.         NA
 6 VDE   ets    2013-12-31 05:00:00    NA    NA    NA -201.         NA
 7 VDE   ets    2013-12-31 06:00:00    NA    NA    NA -180.         NA
 8 VDE   ets    2013-12-31 07:00:00    NA    NA    NA -102.         NA
 9 VDE   ets    2013-12-31 08:00:00    NA    NA    NA   46.9        NA
10 VDE   ets    2013-12-31 09:00:00    NA    NA    NA  230.         NA
# … with 68,245 more rows

Приклад: електроенергія України

energy_fit %>%
  filter(type == "VDE") %>%
  components(energy_fit) %>%
  autoplot()

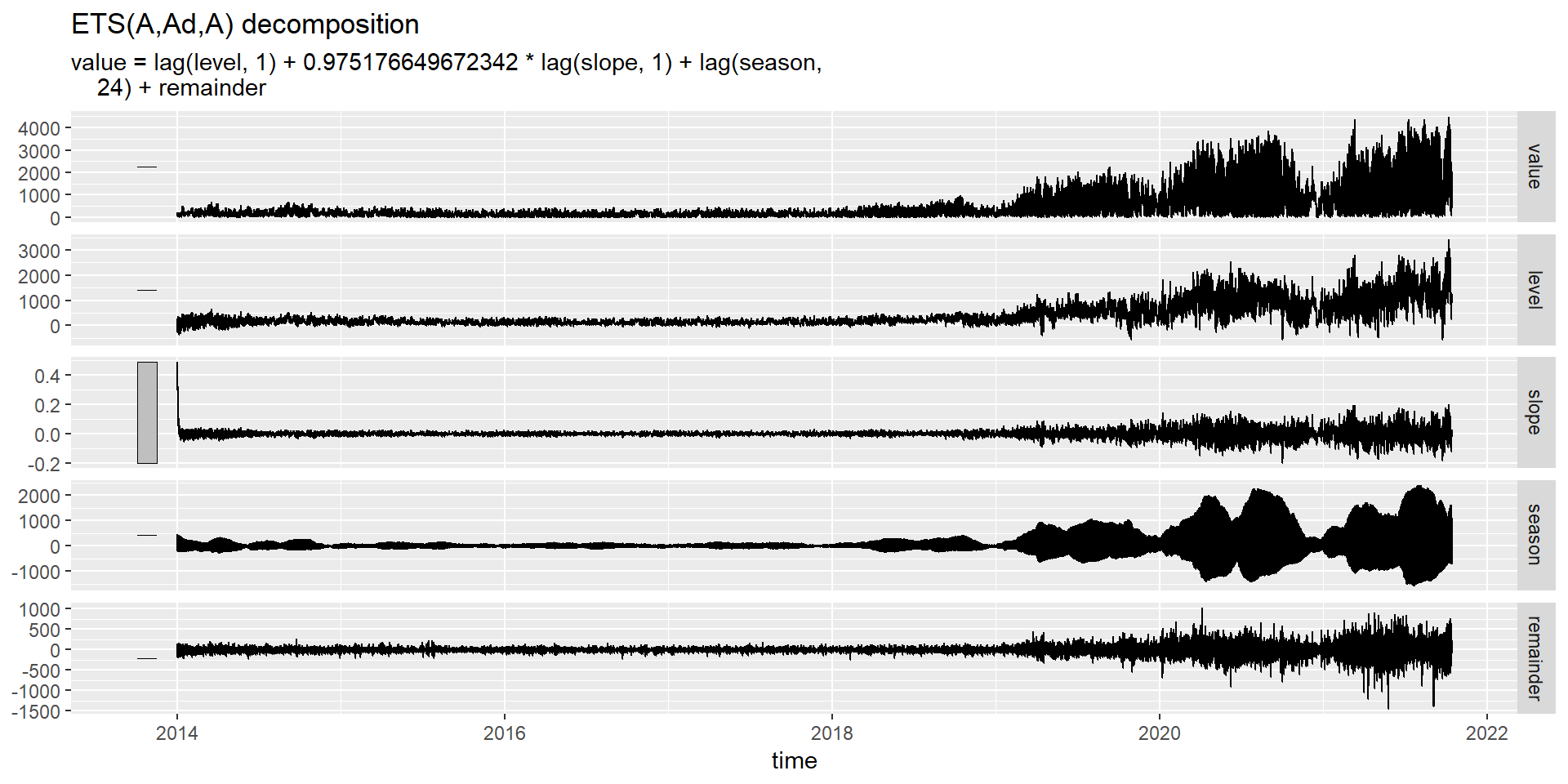
Приклад: електроенергія України

energy_fit %>% forecast()

# A fable: 528 x 5 [1h] <UTC>
# Key:     type, .model [11]
   type  .model time                         value .mean
   <chr> <chr>  <dttm>                      <dist> <dbl>
 1 AES   ets    2021-10-13 23:00:00  N(9951, 2205) 9951.
 2 AES   ets    2021-10-14 00:00:00  N(9951, 4687) 9951.
 3 AES   ets    2021-10-14 01:00:00  N(9951, 7403) 9951.
 4 AES   ets    2021-10-14 02:00:00 N(9951, 10312) 9951.
 5 AES   ets    2021-10-14 03:00:00 N(9951, 13382) 9951.
 6 AES   ets    2021-10-14 04:00:00 N(9951, 16584) 9951.
 7 AES   ets    2021-10-14 05:00:00 N(9951, 19892) 9951.
 8 AES   ets    2021-10-14 06:00:00 N(9951, 23287) 9951.
 9 AES   ets    2021-10-14 07:00:00 N(9951, 26753) 9951.
10 AES   ets    2021-10-14 08:00:00 N(9951, 30276) 9951.
# … with 518 more rows

Приклад: електроенергія України

energy_fit %>%
  forecast() %>%
  filter(type == "VDE") %>%
  autoplot(energy %>% filter_index("2021-09-01" ~ .)) +
  labs(title = "Прогноз соживання ВДЕ України", y = "МВт", x = NULL)

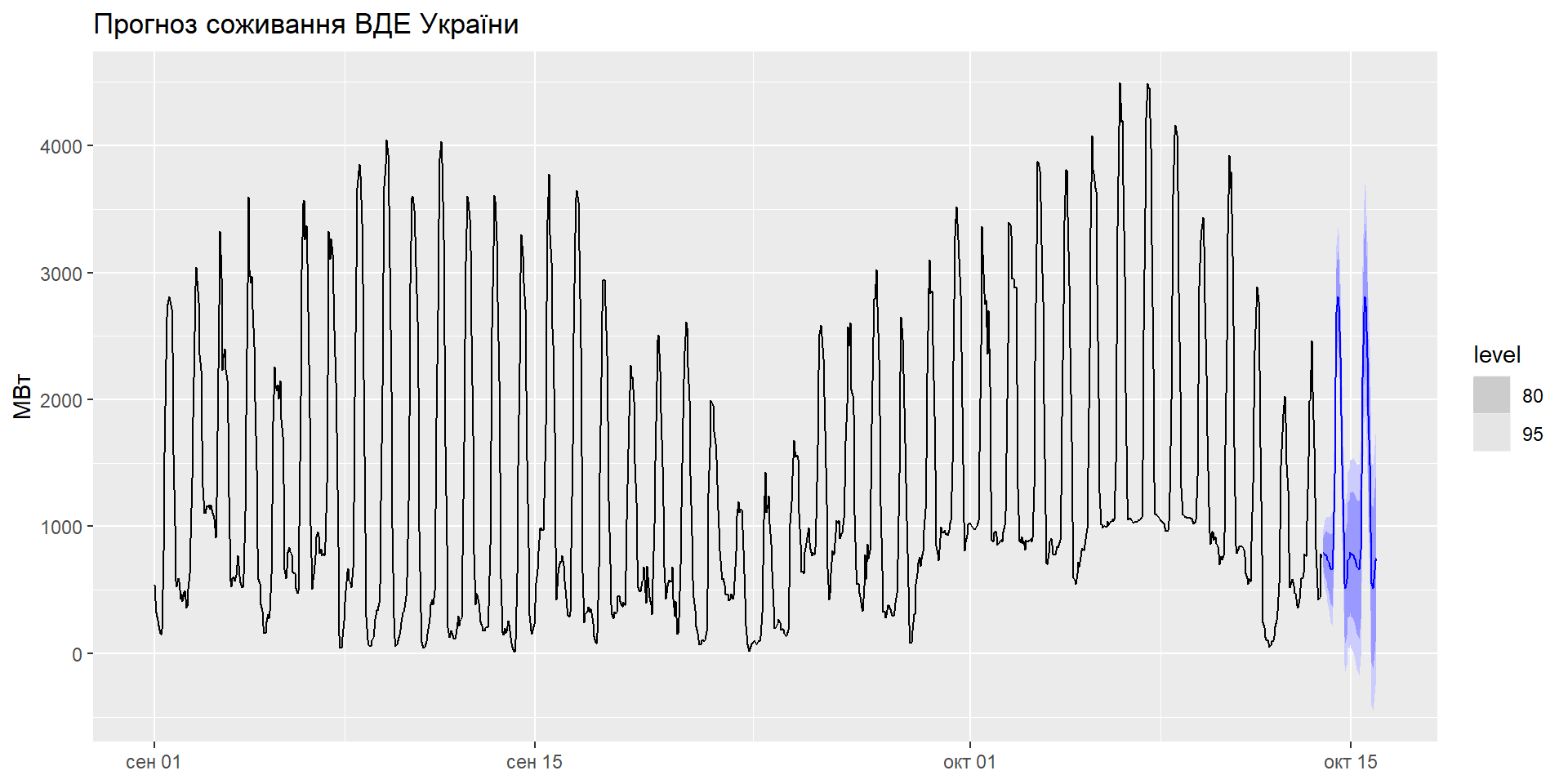
Залишки

Звичайні: \[\hat{e}_t = y_t - \hat{y}_{t|t-1}\]

Просунуті (іноваційні): * Адитивні \[\hat\varepsilon_t = y_t - \hat{y}_{t|t-1}\]

Мультиплікативні \[\hat\varepsilon_t = \frac{y_t - \hat{y}_{t|t-1}}{\hat{y}_{t|t-1}}\]

Приклад: електроенергія України

tes_fit <- energy_fit %>%
  filter(type == "TES") %>%
  report()

Series: value 
Model: ETS(M,N,M) 
  Smoothing parameters:
    alpha = 0.8509127 
    gamma = 0.1386315 

  Initial states:
     l[0]     s[0]    s[-1]    s[-2]    s[-3]    s[-4]    s[-5]    s[-6]
 7215.222 0.885151 1.077347 0.906587 1.020852 1.181553 1.067999 1.252148
    s[-7]    s[-8]    s[-9]   s[-10]   s[-11]   s[-12]   s[-13]    s[-14]
 1.159245 1.212238 1.129374 1.207462 1.174475 1.162923 1.064444 0.9882759
    s[-15]    s[-16]   s[-17]    s[-18]    s[-19]    s[-20]    s[-21]    s[-22]
 0.9559876 0.9943594 0.944768 0.8241083 0.7233081 0.7095042 0.7773208 0.7607846
    s[-23]
 0.8197847

  sigma^2:  0.0021

    AIC    AICc     BIC 
1508282 1508282 1508528

Приклад: електроенергія України

residuals(tes_fit)
residuals(tes_fit, type = "response")

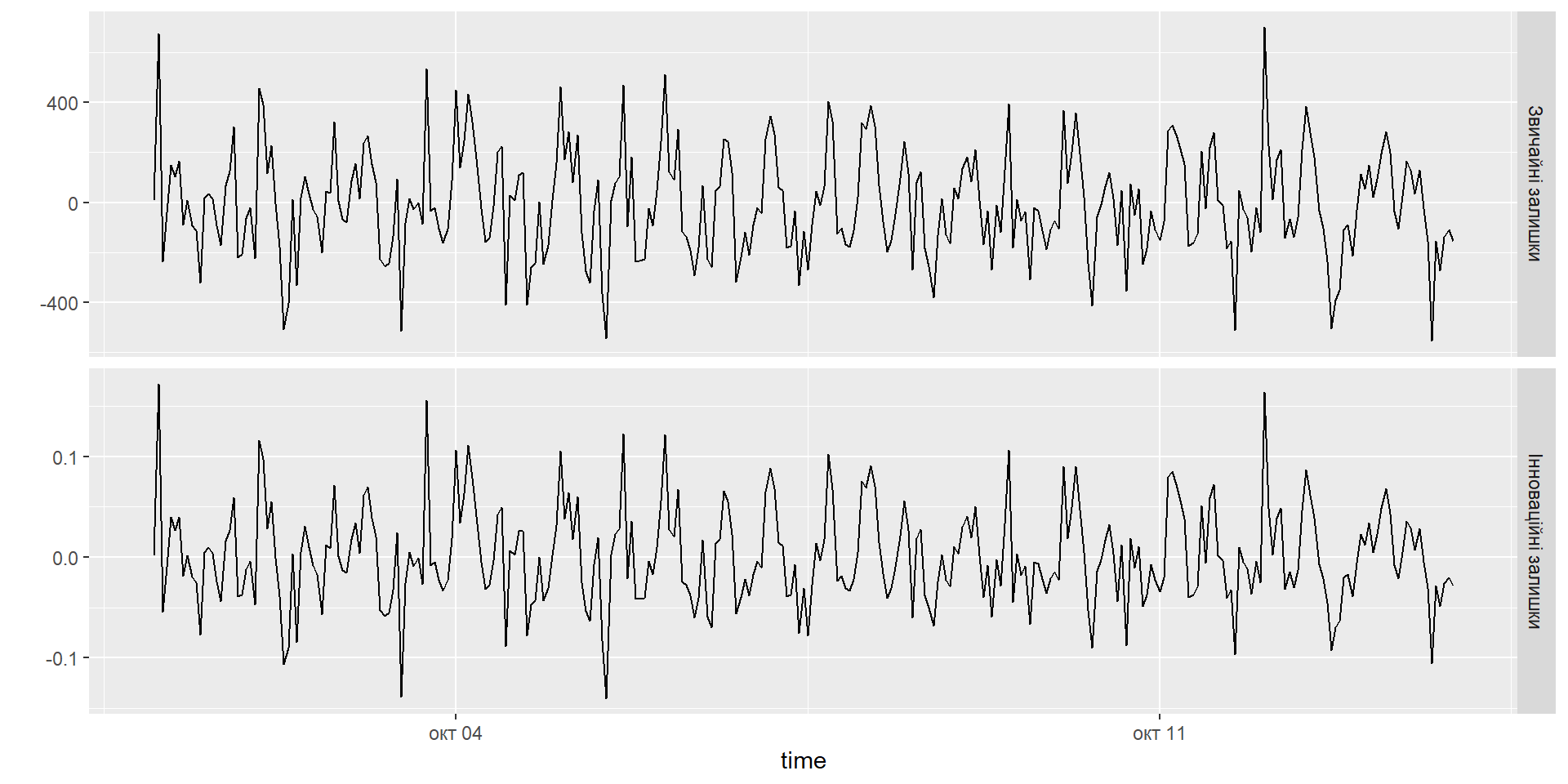
Приклад: електроенергія України

.code70[

tes_fit %>%
  augment()

# A tsibble: 68,231 x 7 [1h] <UTC>
# Key:       type, .model [1]
   type  .model time                value .fitted .resid  .innov
   <chr> <chr>  <dttm>              <dbl>   <dbl>  <dbl>   <dbl>
 1 TES   ets    2014-01-01 00:00:00  6044   5915.  129.   0.0218
 2 TES   ets    2014-01-01 01:00:00  6038   5591.  447.   0.0799
 3 TES   ets    2014-01-01 02:00:00  5865   6101. -236.  -0.0387
 4 TES   ets    2014-01-01 03:00:00  5524   5385.  139.   0.0257
 5 TES   ets    2014-01-01 04:00:00  5506   5610. -104.  -0.0186
 6 TES   ets    2014-01-01 05:00:00  5346   6291. -945.  -0.150 
 7 TES   ets    2014-01-01 06:00:00  5343   6290. -947.  -0.151 
 8 TES   ets    2014-01-01 07:00:00  5324   5772. -448.  -0.0776
 9 TES   ets    2014-01-01 08:00:00  5366   5183.  183.   0.0354
10 TES   ets    2014-01-01 09:00:00  5431   5519.  -88.0 -0.0159
# … with 68,221 more rows

Деякі нестабільні моделі

Деякі комбінації (Error, Trend, Seasonal) можуть призвести до чисельних труднощів;
Це: ETS(A,N,M), ETS(A,A,M), ETS(A,Ad,M);
Моделі з мультиплікативними помилками корисні для позитивних даних, але є нестабільними з даними, що містять нулі або від’ємні значення. У цьому випадку будуть застосовані лише шість повністю адитивних моделей.

Прогнозування з експоненціальним згладжуванням

Прогнозування з ETS моделями

Традиційний точковий прогноз: повторіть рівняння для $t=T+1,T+2,\dots,T+h$ і встановіть усі $\varepsilon_t=0$ для $t>T$.

Довірчі інтервали: можна отримати лише за допомогою моделей.

ДІ будуть відрізнятися між моделями з адитивними та мультиплікативними помилками.

Для більшості ETS моделей ДІ: \[\hat{y}_{T+h|T} \pm c \sigma_h\] де $c$ - показник ймовірності, а $\sigma_h$ стандартне відхилення прогнозу

Прогнозування з ETS моделями

Для ETS моделей стандартне відхилення розраховується залежно від моделі, наприклад:

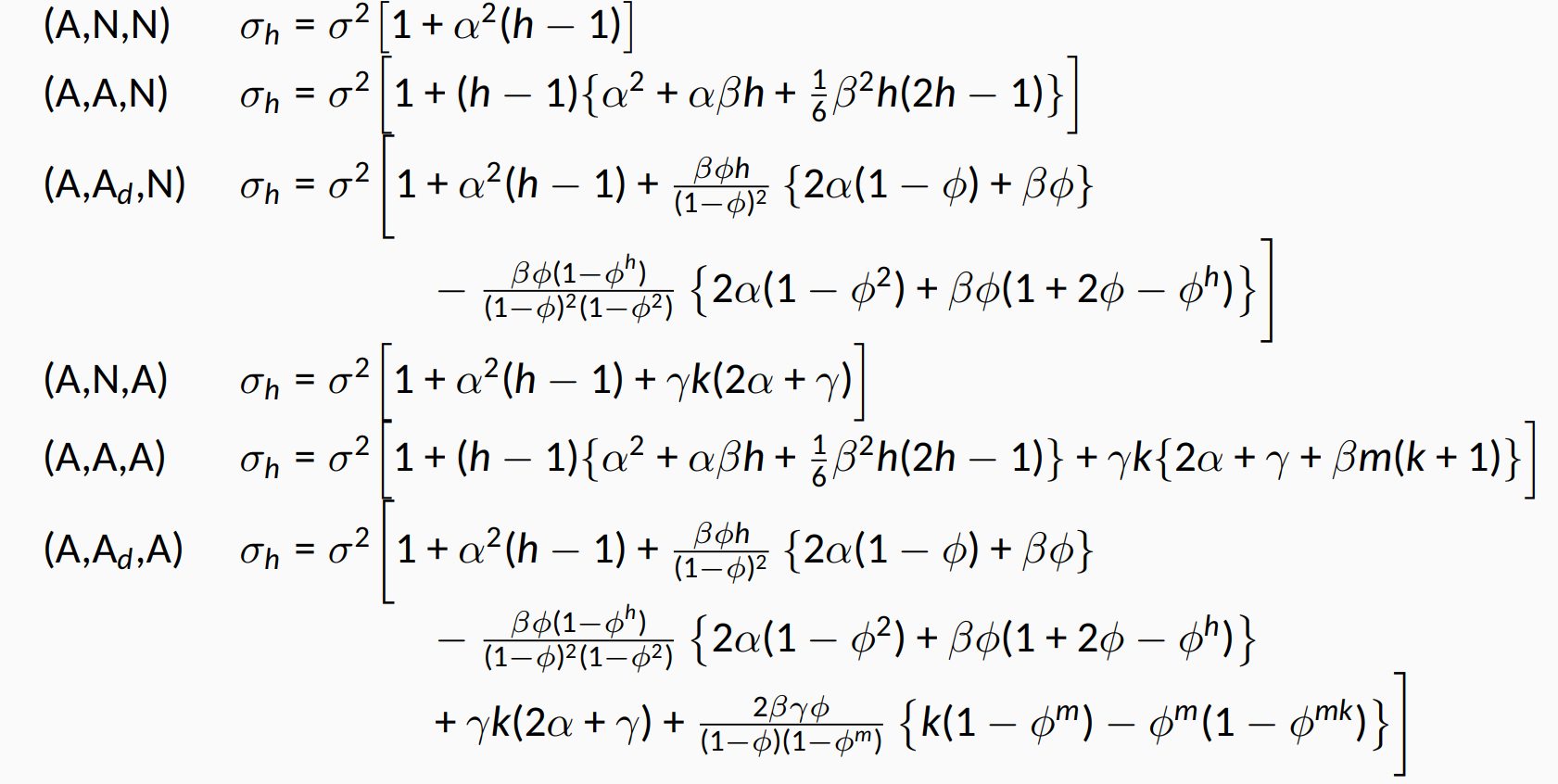
Приклад: продаж ліків

h02 <- PBS %>%
  filter(ATC2 == "H02") %>%
  summarise(Cost = sum(Cost))
h02 %>%
  autoplot(Cost)

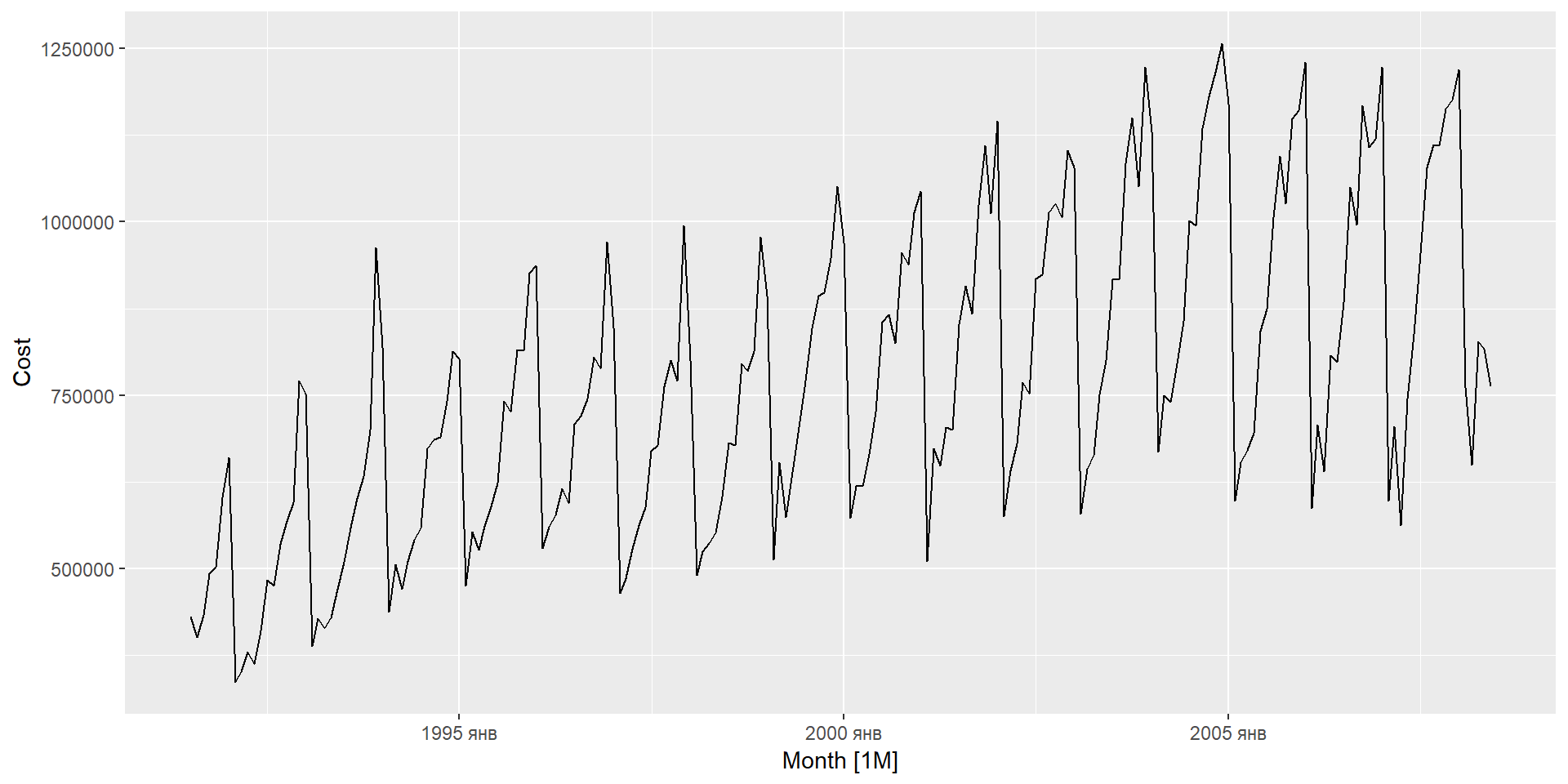
Приклад: продаж ліків

h02 %>%
  model(ETS(Cost)) %>%
  report()

Series: Cost 
Model: ETS(M,Ad,M) 
  Smoothing parameters:
    alpha = 0.3071016 
    beta  = 0.0001006793 
    gamma = 0.0001007181 
    phi   = 0.977528 

  Initial states:
     l[0]    b[0]      s[0]     s[-1]     s[-2]     s[-3]
 417268.7 8205.82 0.8716807 0.8259747 0.7562808 0.7733338
     s[-4]    s[-5]    s[-6]    s[-7]    s[-8]    s[-9]   s[-10]
 0.6872373 1.283821 1.324616 1.180067 1.163601 1.104801 1.047963
    s[-11]
 0.9806235

  sigma^2:  0.0046

     AIC     AICc      BIC 
5515.212 5518.909 5574.938

Приклад: продаж ліків

h02 %>%
  model(ETS(Cost ~ error("A") + trend("A") + season("A"))) %>%
  report()

Series: Cost 
Model: ETS(A,A,A) 
  Smoothing parameters:
    alpha = 0.1702163 
    beta  = 0.006310854 
    gamma = 0.4545987 

  Initial states:
     l[0]     b[0]      s[0]     s[-1]     s[-2]     s[-3]
 409705.9 9097.111 -99075.37 -136602.3 -191496.1 -174530.8
     s[-4]    s[-5]    s[-6]    s[-7]    s[-8]    s[-9]  s[-10]
 -241436.7 210643.8 244644.2 145368.2 130569.6 84457.69 39131.7
    s[-11]
 -11673.71

  sigma^2:  3498869384

     AIC     AICc      BIC 
5585.278 5588.568 5641.686

Приклад: продаж ліків

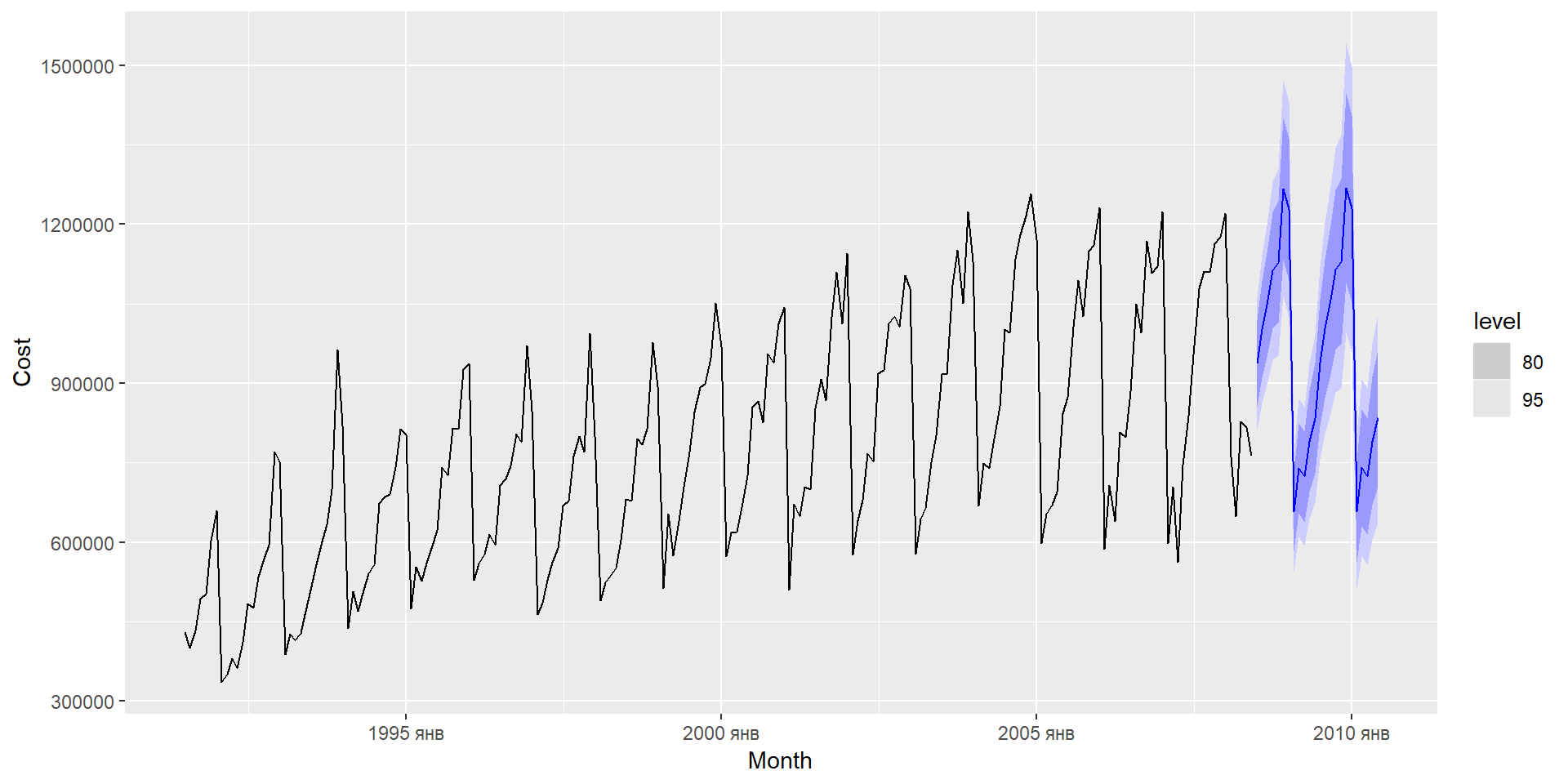
h02 %>% model(ETS(Cost)) %>% forecast() %>% autoplot(h02)

Приклад: продаж ліків

h02 %>%
  model(
    auto = ETS(Cost),
    AAA = ETS(Cost ~ error("A") + trend("A") + season("A"))
  ) %>%
  accuracy()

Model	MAE	RMSE	MAPE	MASE	RMSSE
auto	38649.04	51102.24	4.988983	0.6375806	0.6891173
AAA	43378.40	56784.23	6.047574	0.7155993	0.7657394

Дякую за увагу!

ihor.miroshnychenko@kneu.ua

Спостереження	\(\alpha = 0.2\)	\(\alpha = 0.4\)	\(\alpha = 0.6\)	\(\alpha = 0.8\)
\(y_t\)	0.2	0.4	0.6	0.8
\(y_{t-1}\)	0.16	0.24	0.24	0.16
\(y_{t-2}\)	0.128	0.144	0.096	0.032
\(y_{t-3}\)	0.1024	0.0864	0.0384	0.0064
\(y_{t-4}\)	0.0819	0.0518	0.0154	0.0013
\(y_{t-5}\)	0.0655	0.0311	0.0061	0.0003