04 - Декомпозиція часових рядів
Прогнозування часових рядів
Ігор Мірошниченко
КНЕУ::ІІТЕ
оновлено: 2022-10-11
Перетворення часових рядів
На душу населення
Коригування на інфляцію
Товар, куплений сьогодні за умовні ₴10,000 це не те саме, що ₴10,000 десять років назад.
Тому досить часто ціни на товар приводять до базового року.
Для створення таких коригувань використовують індекс цін.
Якщо \(z_t\) - це індекс цін, а \(y_t\) - ціна товару у \(t\) році, тоді скорегована ціна: \[x_t=y_t/z_t*z_{t-k}\]
Коригування на інфляцію
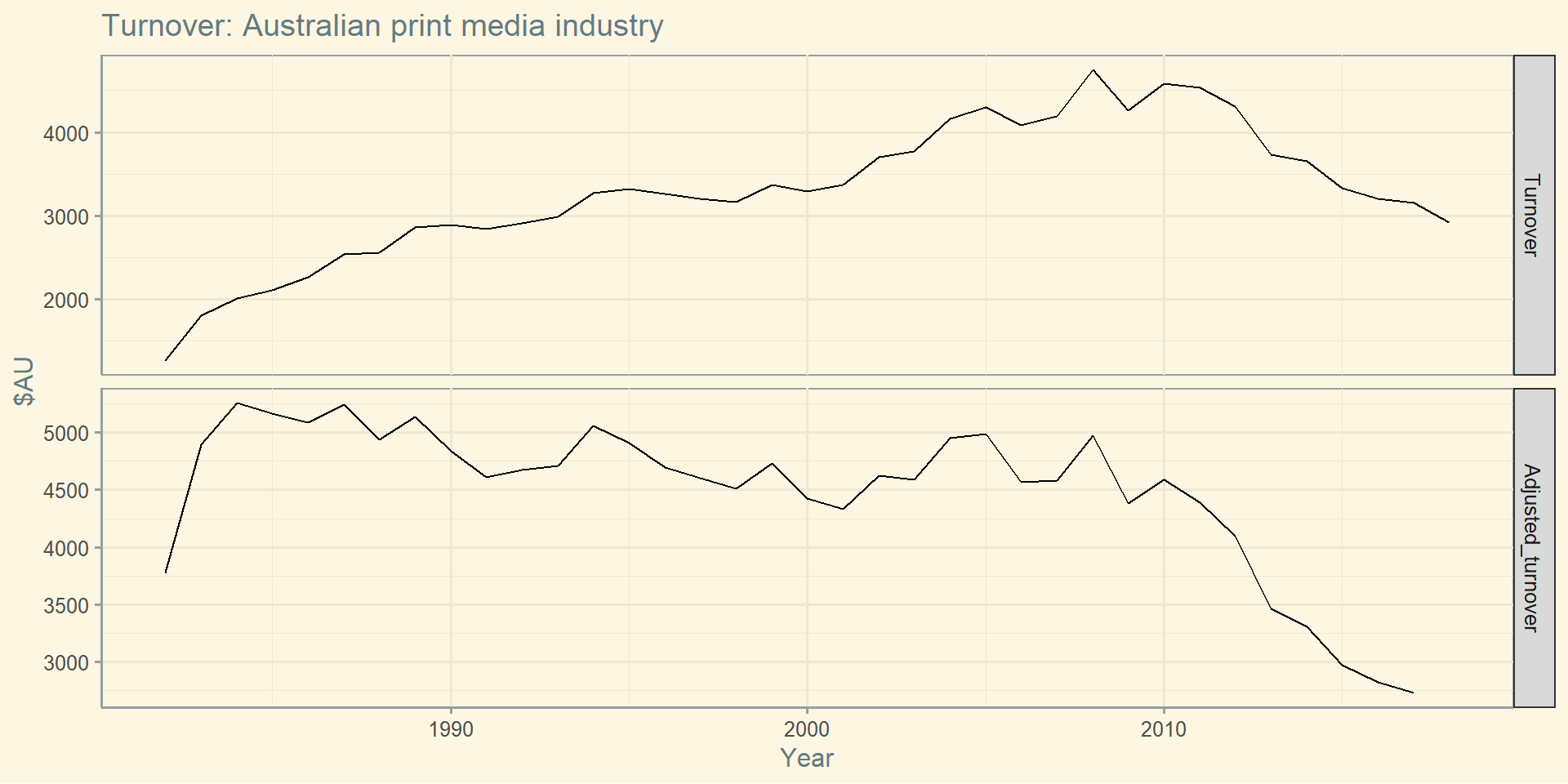
Математичні перетворення
Якщо спостерігається різна дисперсія на різних рівнях часового ряду є сенс використати перетворення даних.
В такому випадку ориріганльні дані \(y_1,y_2,...,y_n\) перетворюються у \(w_1,w_2,...,w_n\) за певною формулою або правилом.
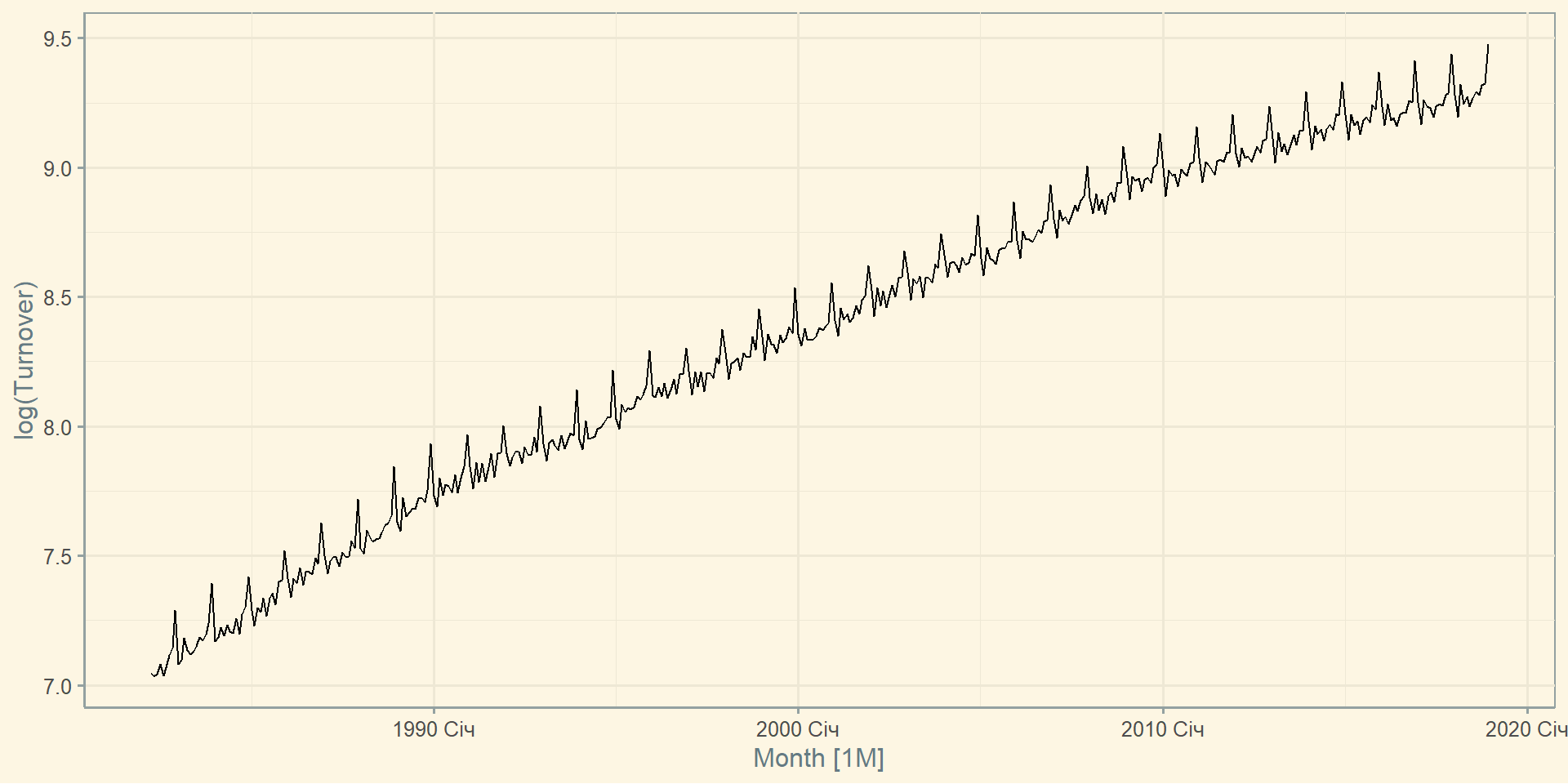
Наприклад через лагорифмування, \(w_t = log(y_t)\)
Математичні перетворення
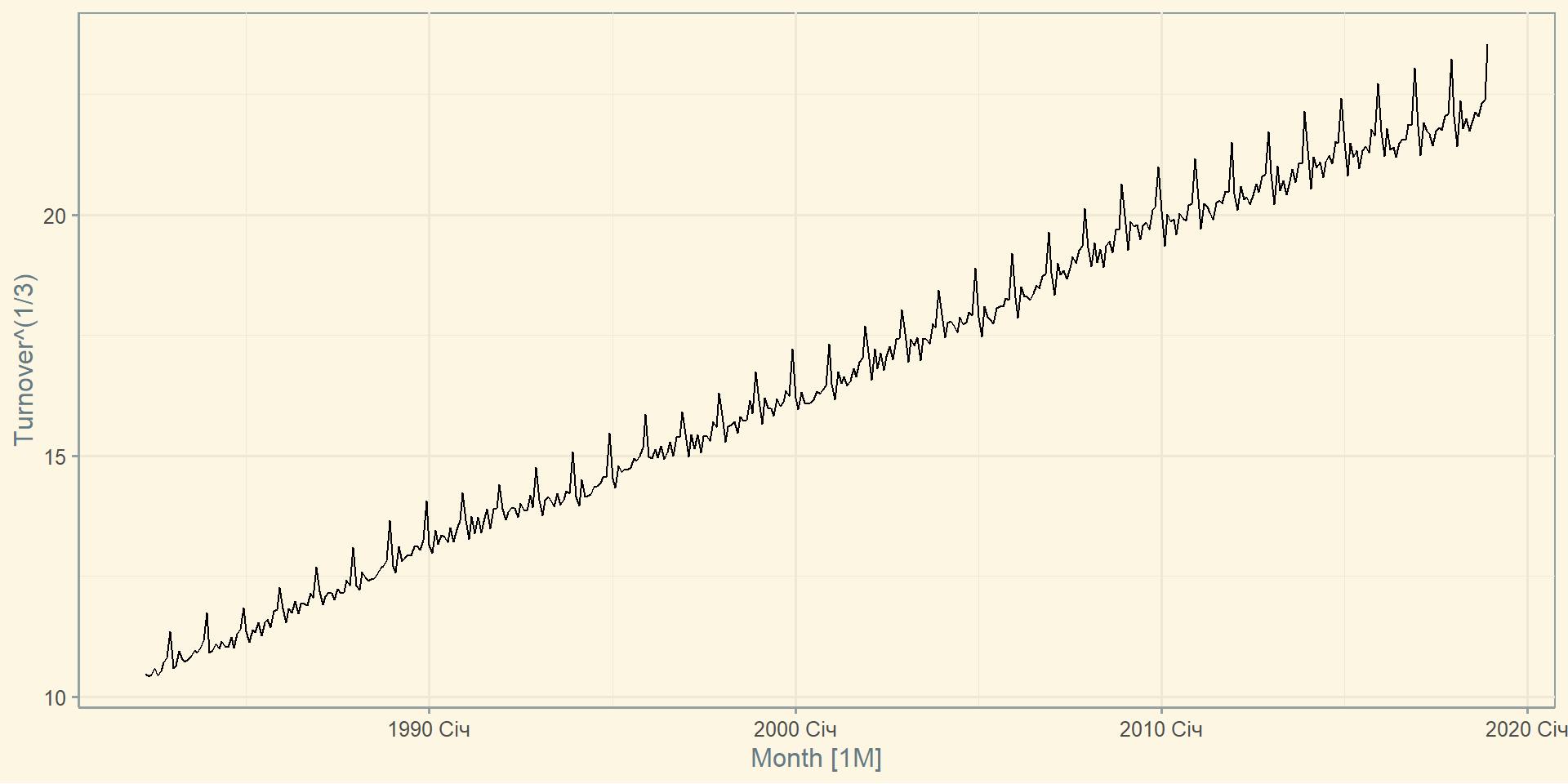
Існують й інші методи перетворення даних. Наприклад корінь квадратний, кубічний корінь тощо.
| Назва | Формула | Сила перетворення |
|---|---|---|
| Корінь квадратний | \(w_t = \sqrt{y_t}\) | \(\downarrow\) |
| Корінь кубічний | \(w_t = \sqrt[3]{y_t}\) | Збільшення |
| Логарифм | \(w_t = \log(y_t)\) | сили |
Логарифми корисні, оскільки їх можна інтерпретувати: зміна значень на 1 у логарифмі відповідає множенню на 10 у реальних значеннях.
Математичні перетворення
Перетворення Бокса-Кокса
Корисним сімейством перетворень, що включає як логарифми, так і степенні перетворення, є сімейство перетворень Бокса-Кокса, які залежать від параметра \(\lambda\): \[w_t = \begin{cases}log(y_t) & \quad \lambda = 0; \\ (y_t^\lambda-1)/\lambda ,&\quad \lambda \ne 0.\end{cases}\] * \(\lambda=1\): (Без перетворень) * \(\lambda=\frac12\): (Квадратний корінь + лінійне перетворення) * \(\lambda=0\): (Натуральний логарифм) * \(\lambda=-1\): (Зворотнє перетворення + 1)
Перетворення Бокса-Кокса
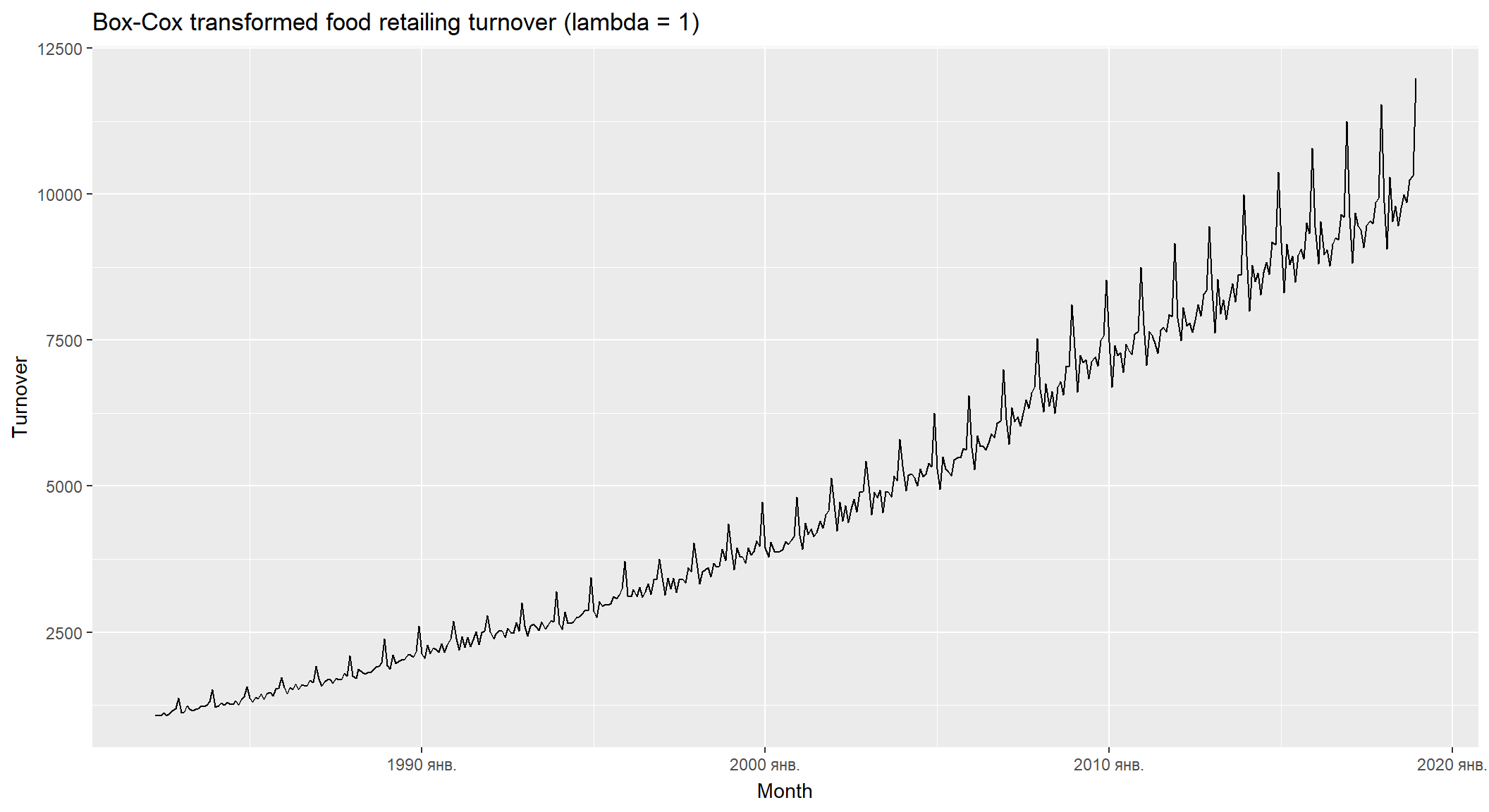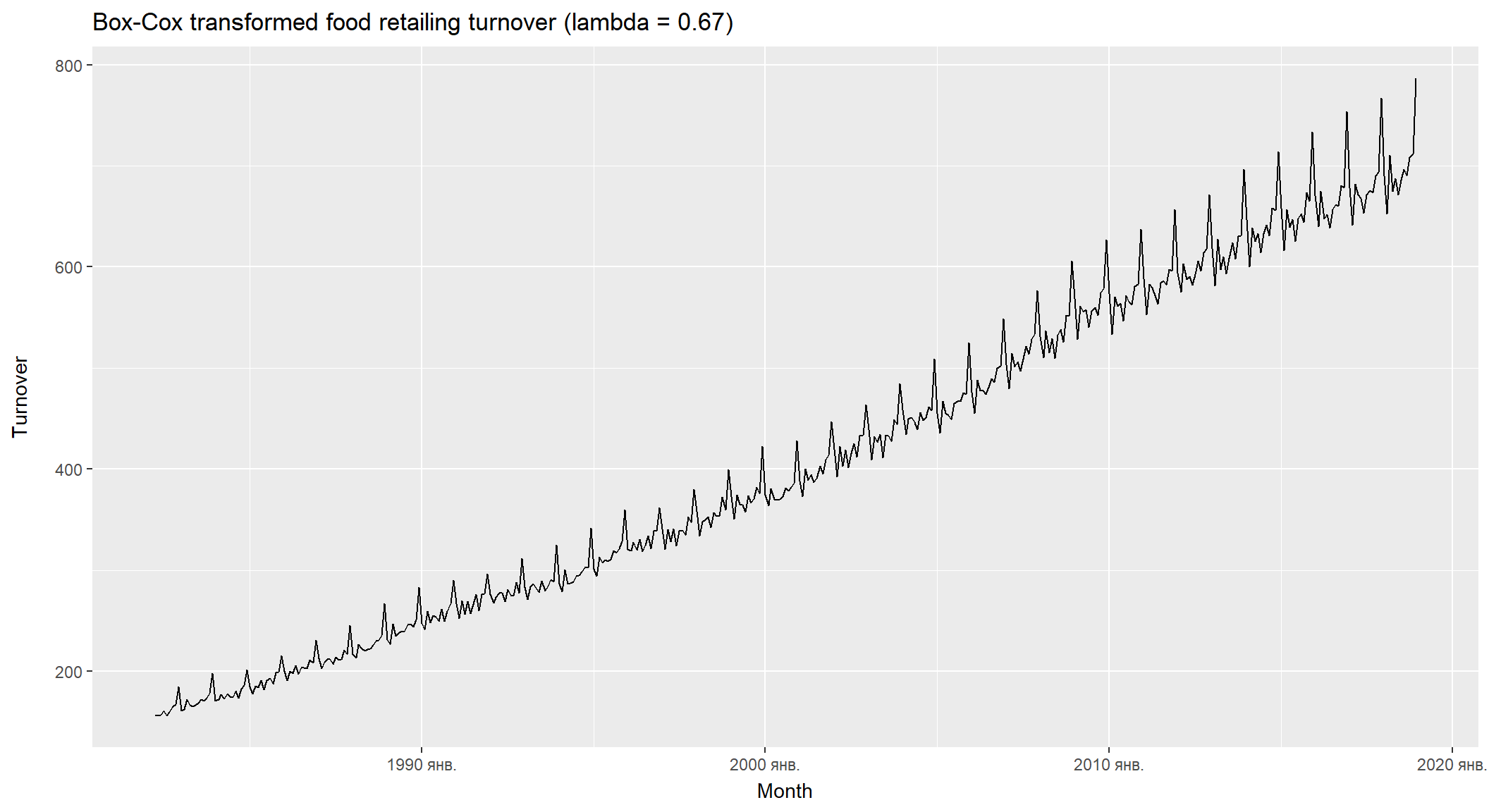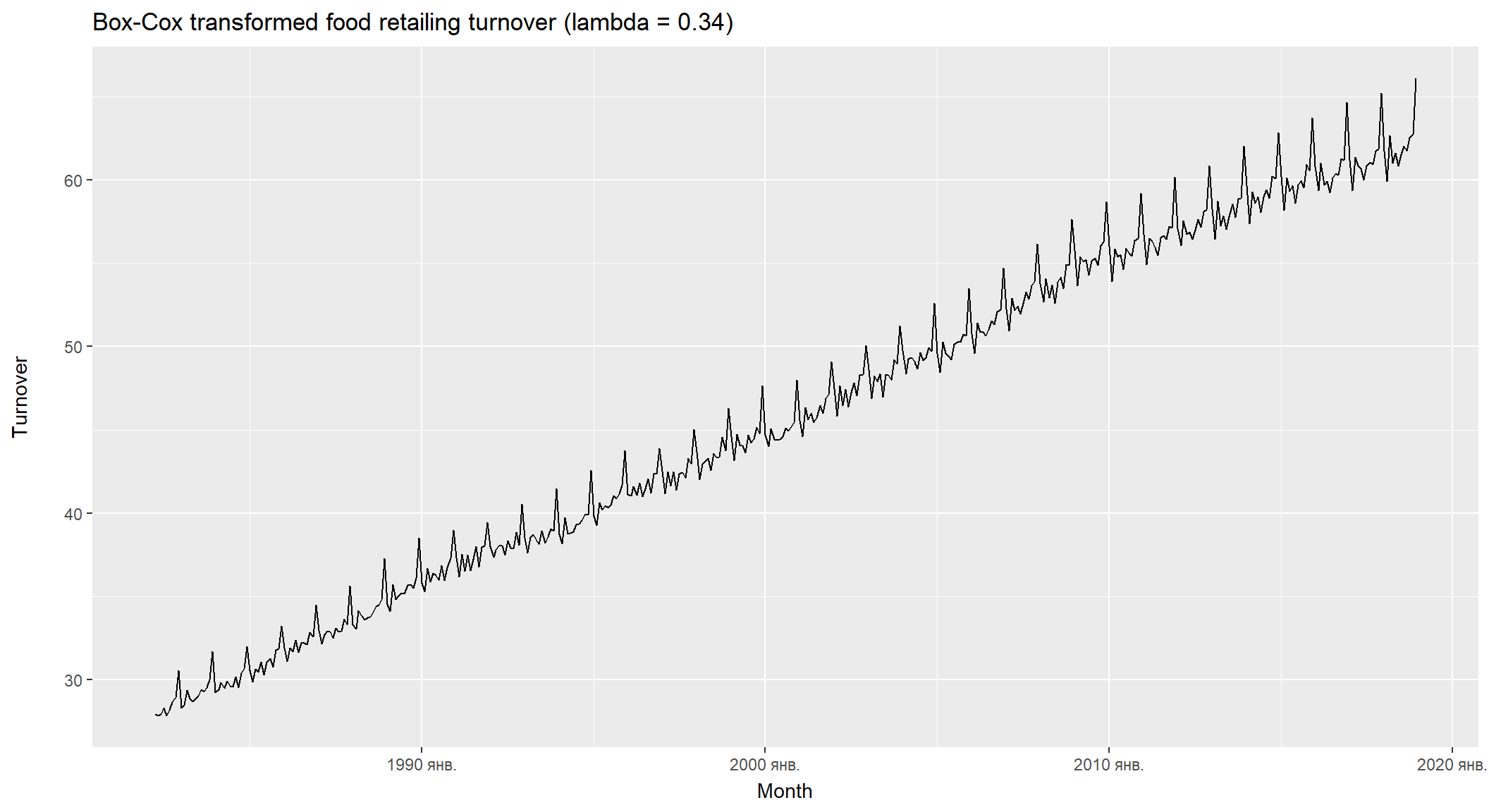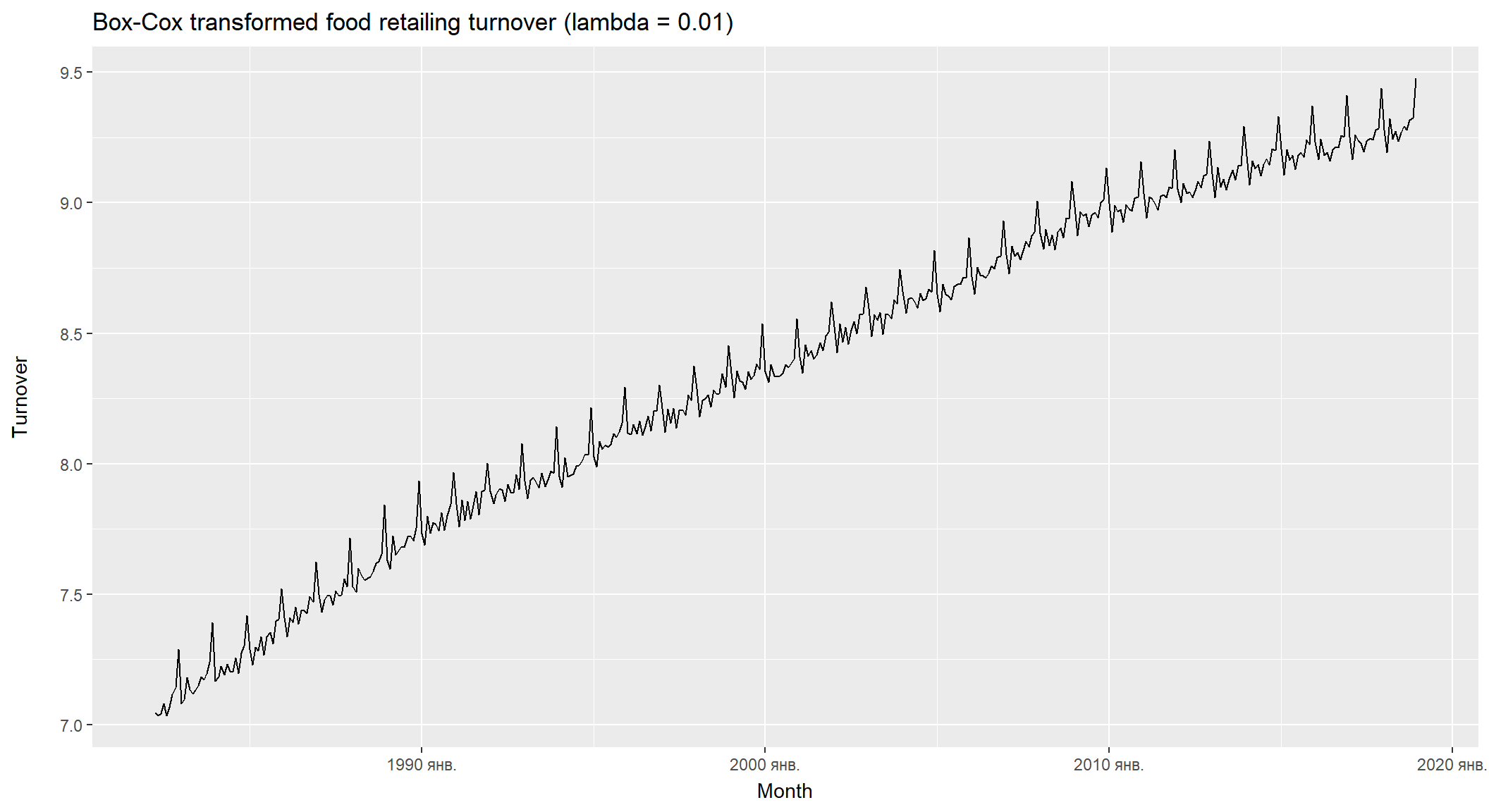
Перетворення Бокса-Кокса
- \(\lambda\) намагається врівноважити сезонні коливання та випадкові зміни у часовому ряді.
- Завжди перевіряйте результати.
- Низьке значення \(\lambda\) може дати надзвичайно великі інтервали прогнозування.
Перетворення Бокса-Кокса
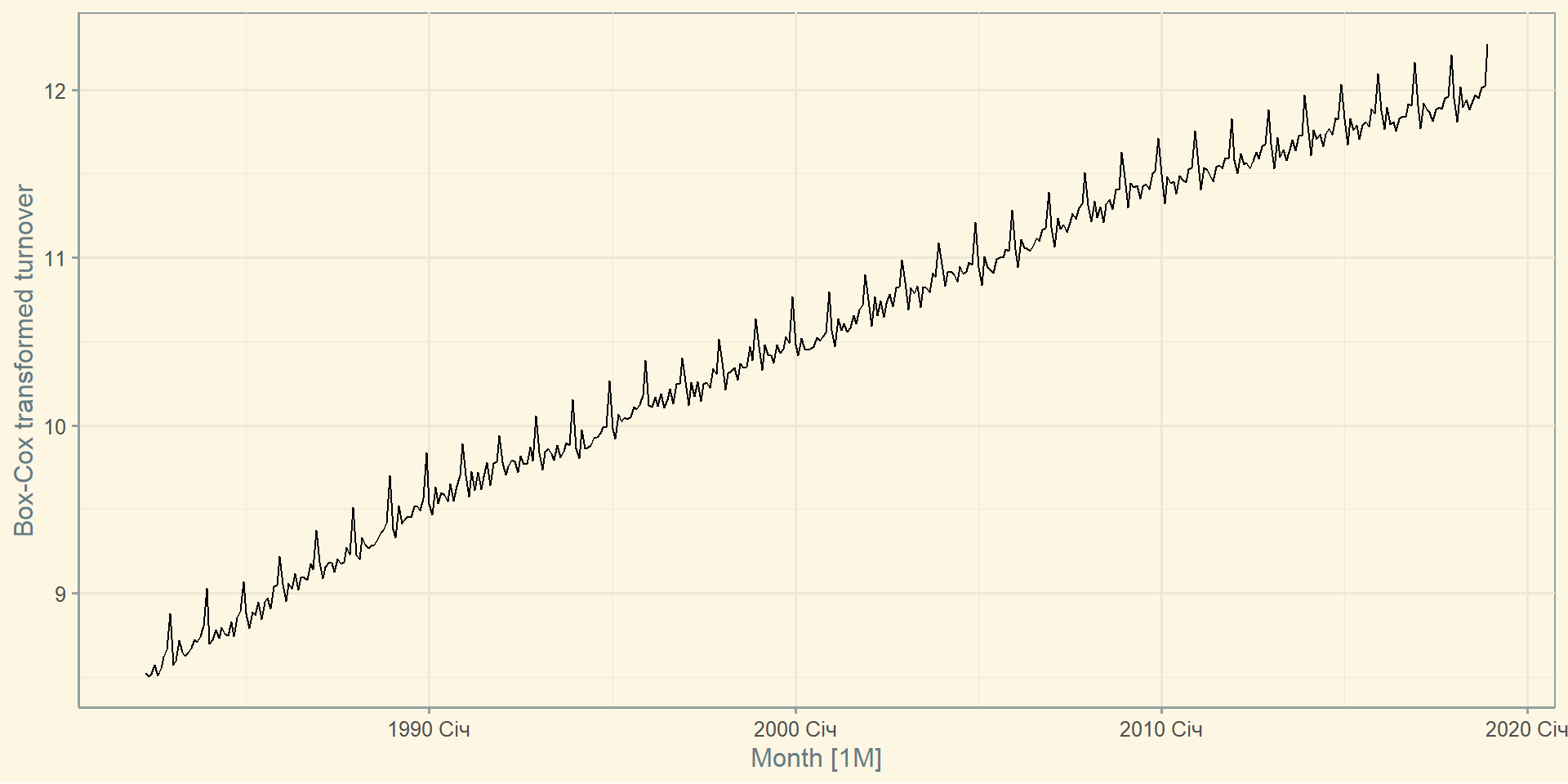
Рекомендації
Часто жодних перетворень не потрібно.
Прості перетворення легше інтерпретувати.
Перетворення можуть мати дуже великий вплив на довірчі інтервали.
Якщо деякі дані нульові або від’ємні, використовуйте \(\lambda> 0\).
log1p()може бути корисним для даних з нулями.Вибір лагу - це простий спосіб змусити прогнози бути позитивними
Для отримання прогнозів у реальній шкалі, необхідно провести зворотнє перетворення (обробляється автоматично у
fable).
Декомпозиція часового ряду
Загальні положення
\[y_t = f(S_t, T_t, R_t)\] де \(y_t=\) часовий ряд в момент часу \(t\)
\(T_t=\) тренд-циклічна компонента в момент часу \(t\)
\(S_t=\) сезонна компонента в момент часу \(t\)
\(R_t=\) залишки в момент часу \(t\)
Адитивна декомпозиція: \(y_t = S_t + T_t + R_t.\)
Мультиплікативна декомпозиція: \(y_t = S_t \times T_t \times R_t.\)
Загальні положення
Адитивна модель підходить, якщо величина сезонних коливань не змінюється залежно від рівня.
Якщо сезонні коливання залежать від рівнів ряду, то краще використовувати мультиплікативну модель.
Мультиплікативна декомпозиція більш поширена в економічних рядах
Альтернатива: використовуйте перетворення Бокса-Кокса, а потім використовуйте адитивну декомпозицію
Логарифми перетворюють мультиплікативну декомпозицію у адитивну:
\[y_t = S_t \times T_t \times R_t \quad\Rightarrow\quad \log y_t = \log S_t + \log T_t + \log R_t.\]
US Retail Employment
us_retail_employment <- us_employment %>%
filter(year(Month) >= 1990, Title == "Retail Trade") %>%
select(-Series_ID)
us_retail_employment# A tsibble: 357 x 3 [1M]
Month Title Employed
<mth> <chr> <dbl>
1 1990 Січ Retail Trade 13256.
2 1990 Лют Retail Trade 12966.
3 1990 Бер Retail Trade 12938.
4 1990 Кві Retail Trade 13012.
5 1990 Тра Retail Trade 13108.
6 1990 Чер Retail Trade 13183.
7 1990 Лип Retail Trade 13170.
8 1990 Сер Retail Trade 13160.
9 1990 Вер Retail Trade 13113.
10 1990 Жов Retail Trade 13185.
# … with 347 more rowsUS Retail Employment
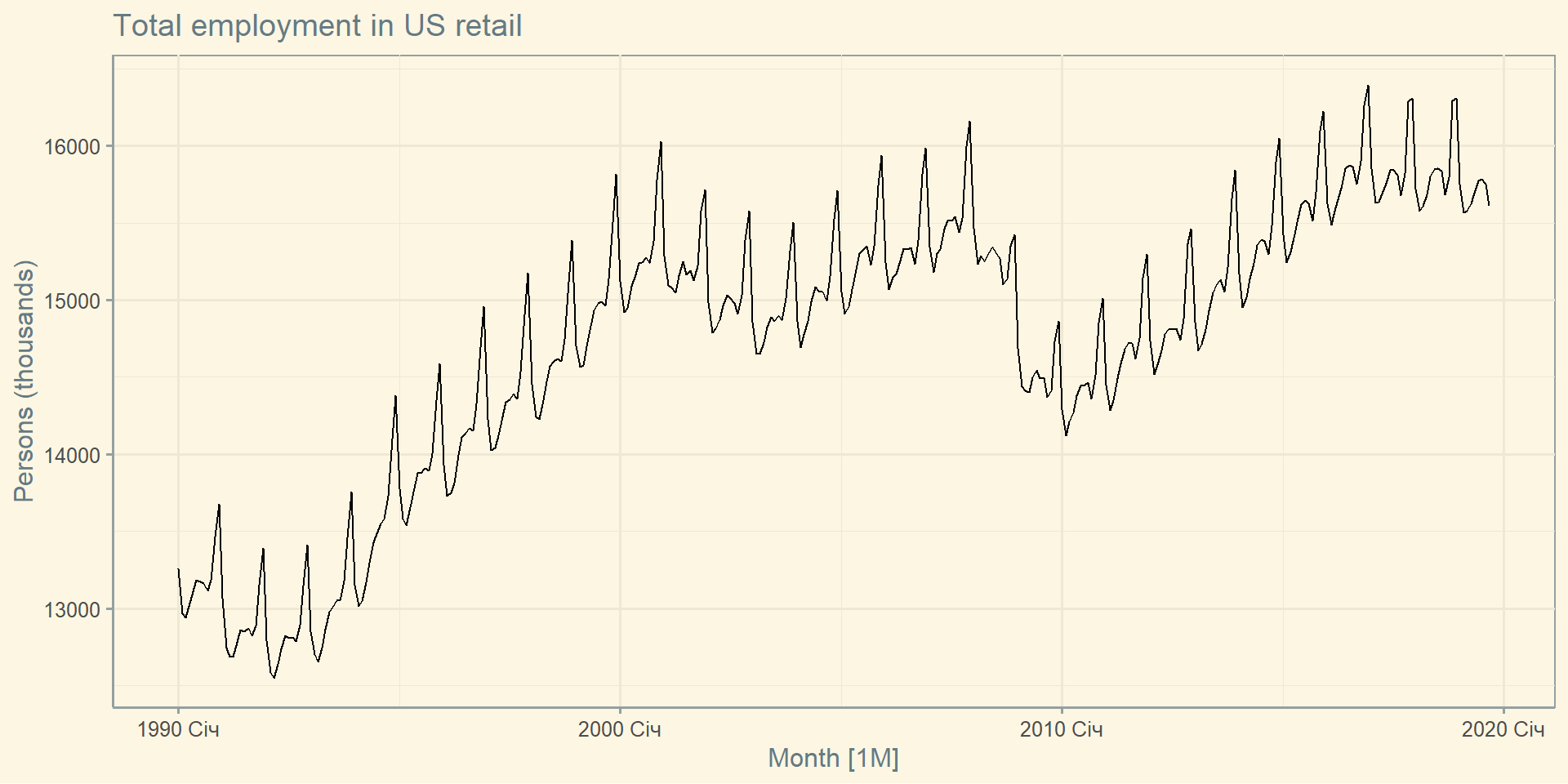
US Retail Employment
US Retail Employment
# A dable: 357 x 7 [1M]
# Key: .model [1]
# : Employed = trend + season_year + remainder
.model Month Employed trend season_year remainder season_adjust
<chr> <mth> <dbl> <dbl> <dbl> <dbl> <dbl>
1 stl 1990 Січ 13256. 13288. -33.0 0.836 13289.
2 stl 1990 Лют 12966. 13269. -258. -44.6 13224.
3 stl 1990 Бер 12938. 13250. -290. -22.1 13228.
4 stl 1990 Кві 13012. 13231. -220. 1.05 13232.
5 stl 1990 Тра 13108. 13211. -114. 11.3 13223.
6 stl 1990 Чер 13183. 13192. -24.3 15.5 13207.
7 stl 1990 Лип 13170. 13172. -23.2 21.6 13193.
8 stl 1990 Сер 13160. 13151. -9.52 17.8 13169.
9 stl 1990 Вер 13113. 13131. -39.5 22.0 13153.
10 stl 1990 Жов 13185. 13110. 61.6 13.2 13124.
# … with 347 more rowsUS Retail Employment
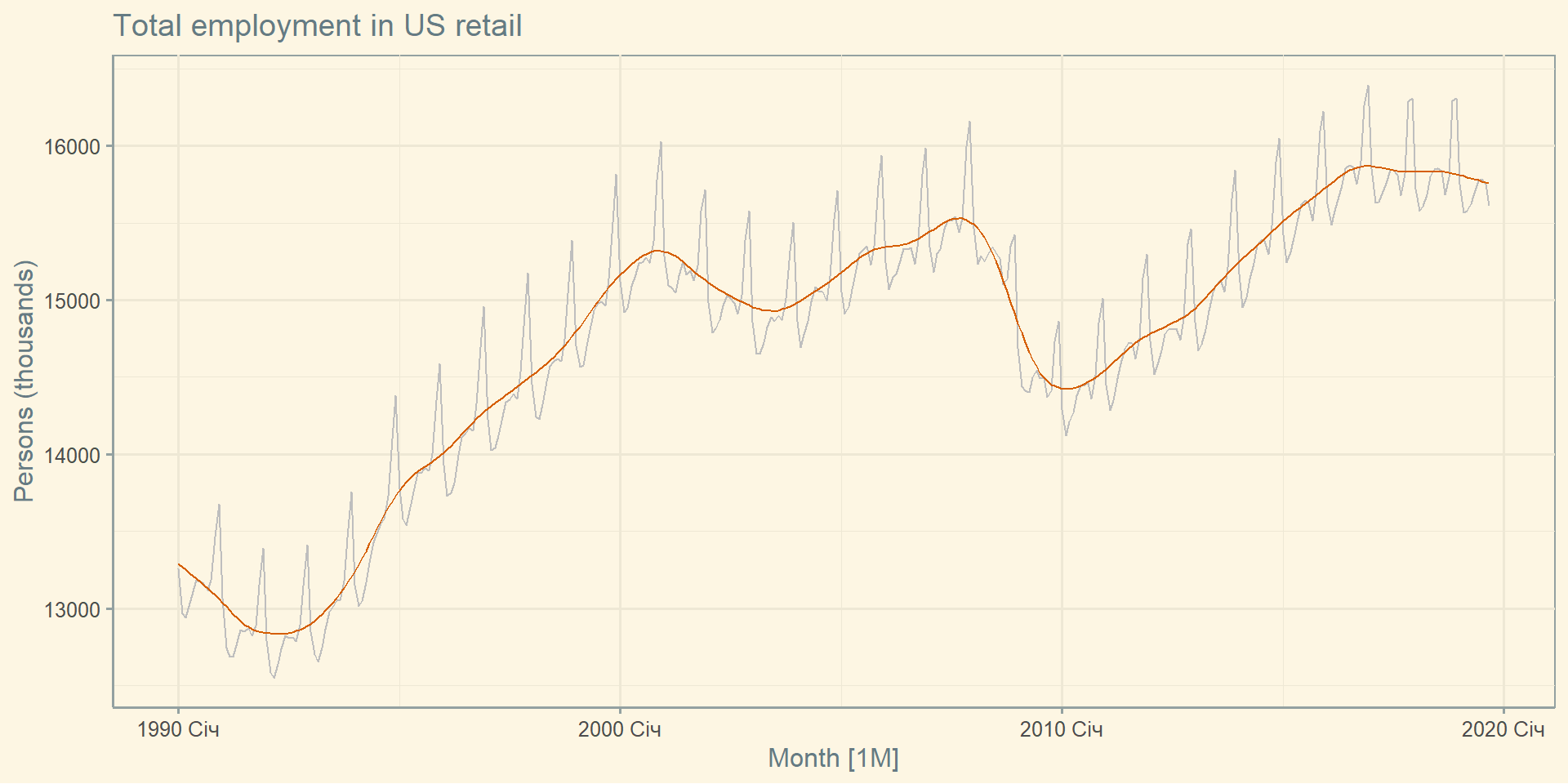
US Retail Employment
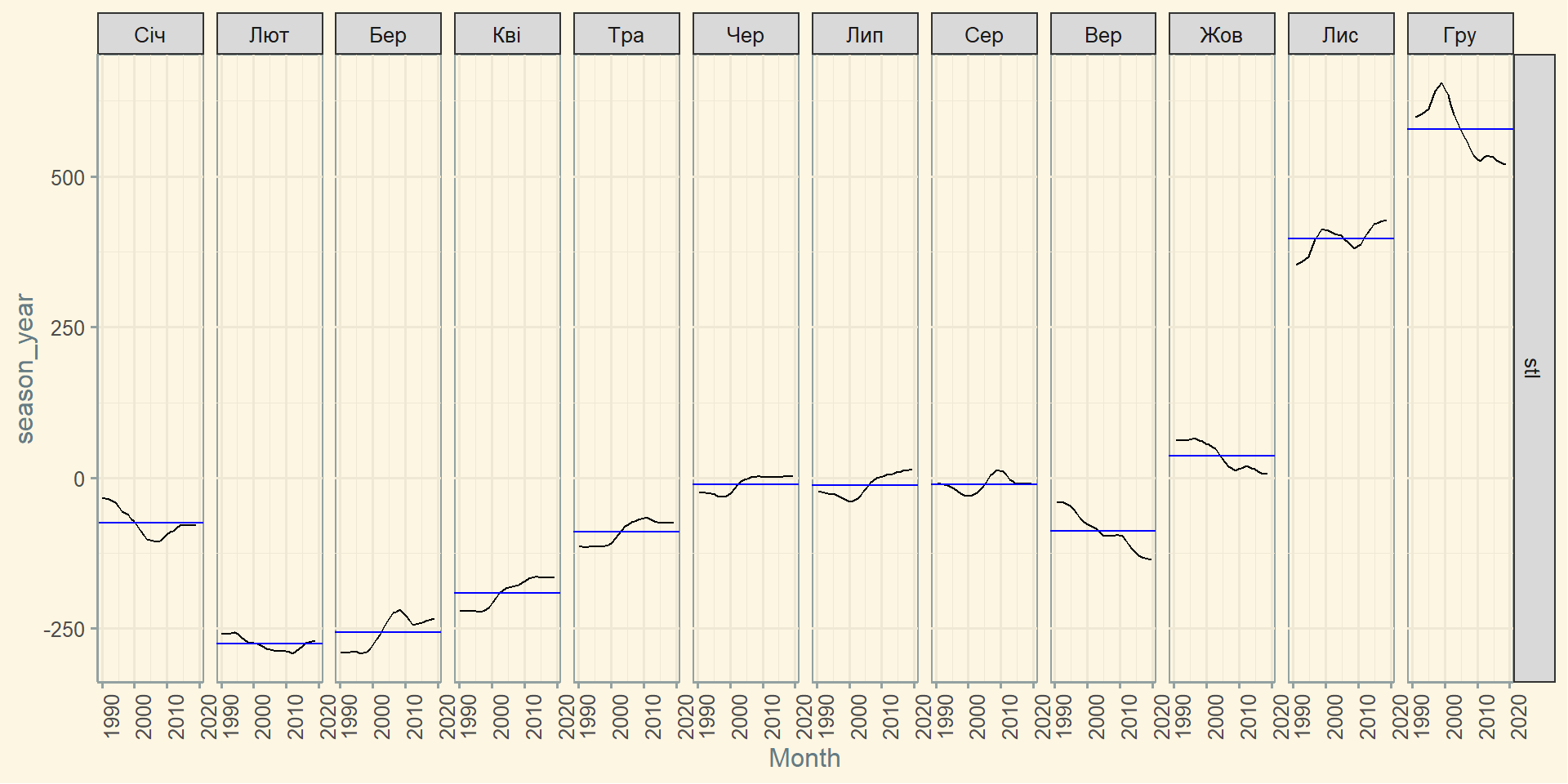
Сезонно-скорегований ряд
Простий спосіб обчислення сезонно скоригованих даних.
Адитивна декомпозиція: \[y_t - S_t = T_t + R_t\]
Мультиплікативна декомпозиція: \[y_t / S_t = T_t \times R_t\]
US Retail Employment
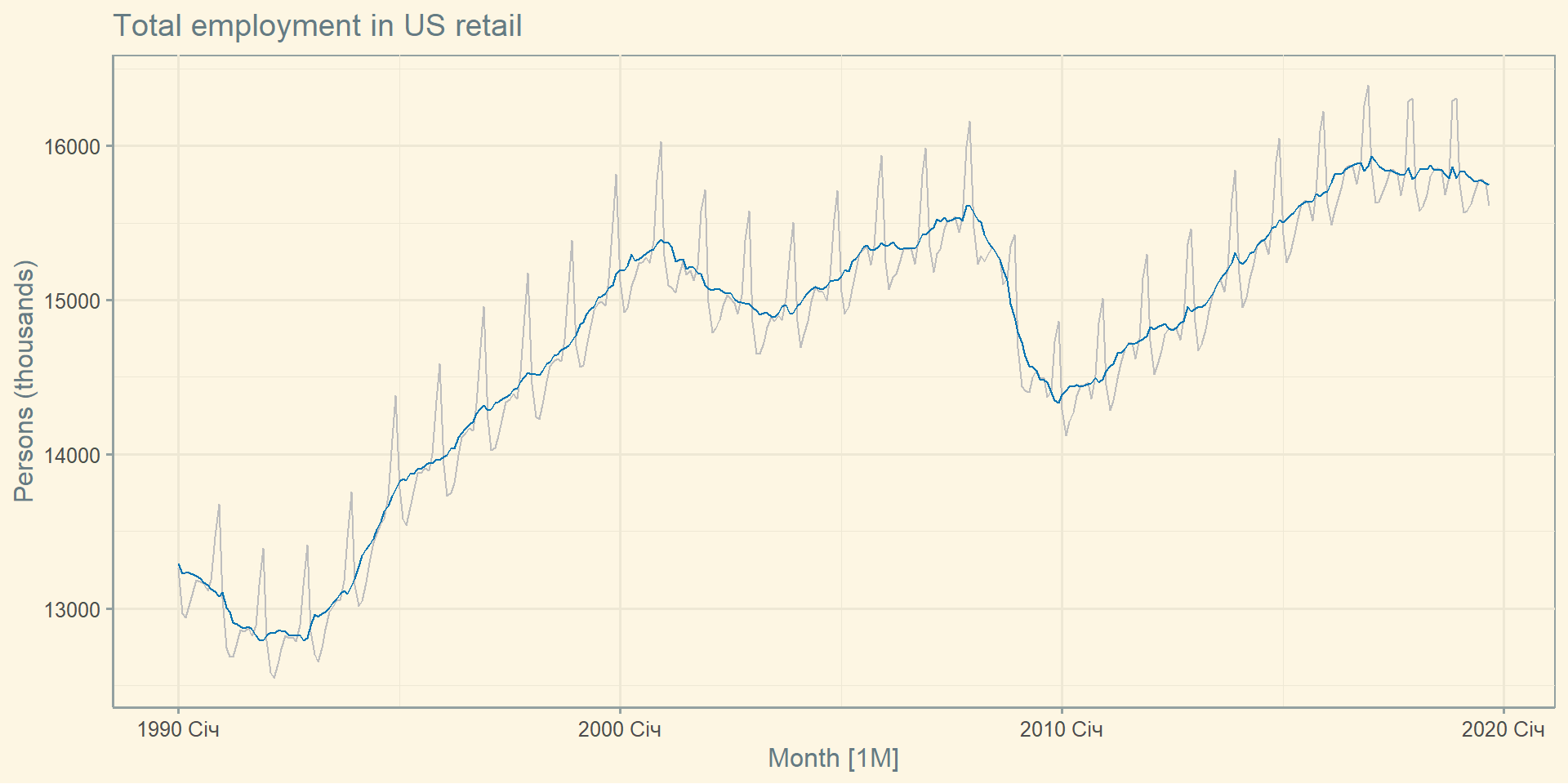
Сезонно-скорегований ряд
Ми використовуємо оцінки \(S\) на основі минулих значень для сезонного коригування поточної вартості.
Сезонно скориговані ряди відображають залишки, а також тенденцію.
Для пошуку поворотних моментів краще використовувати тренд-циклічну компоненту.
Історія декмпозиції часових рядів
Класичний метод виник у 1920-х роках.
Метод Census II введений у 1957 році. Основа для методу X-11 та його варіантів (включаючи X-12-ARIMA, X-13-ARIMA)
Метод STL, запроваджений у 1983 році
TRAMO/SEATS представлені в 1990-х роках.
Національні управління статистики
ABS використовує X-12-ARIMA
Бюро перепису населення США використовує X-13ARIMA-SEATS
Статистичне управління Канади використовує X-12-ARIMA
ONS (Великобританія) використовує X-12-ARIMA
EuroStat використовує X-13ARIMA-SEATS
X-11 декмпозиція
Переваги
Відносно стійка до викидів
Повністю автоматизований підхід для тренду та сезонних змін
Широко впроваджено на економічних даних протягом тривалого періоду часу.
Недоліки
Немає прогнозних/довірчих інтервалів
Спеціальний метод без базової моделі
Розроблено лише для квартальних та місячних даних
Розширення: X-12-ARIMA і X-13-ARIMA
Методи X-11, X-12-ARIMA та X-13-ARIMA засновані на розкладі CENSUS II.
Вони дозволяють коригувати дані відносно торгових днів та інших пояснювальних змінних.
Відомі викиди можна опустити.
Розглядається робота з відсутніми значеннями.
Можна враховувати свята (наприклад, Великдень, День праці).
X-13ARIMA-SEATS
Переваги
На основі моделі
Плавна оцінка тенденції
Дозволяє будувати оцінки на кінець періоду
Дозволяє змінювати сезонність
Розроблено для економічних даних
Недоліки
- Розроблено лише для квартальних та місячних даних
STL декомпозиція
STL декомпозиція
STL: «Сезонна та трендова декомпозиція за допомогою LOESS (“LOcal regrESSions”, метод локальних полиноміальних регресій)
Дуже універсальний і потужний інструмент
На відміну від X-12-ARIMA, STL впорається з будь-яким типом сезонності.
Сезонна компонента може змінюватися з часом, а швидкість змін контролюється користувачем.
Плавність тренд-циклу також контролюється користувачем.
Робаста до викидів
Не потребує коригування торгового дня чи календаря.
Тільки адитивна.
Візьміть логарифми, щоб отримати мультиплікативну декомпозицію.
Використовуйте перетворення Бокса-Кокса, щоб отримати інші декомпозиції.
STL декомпозиція
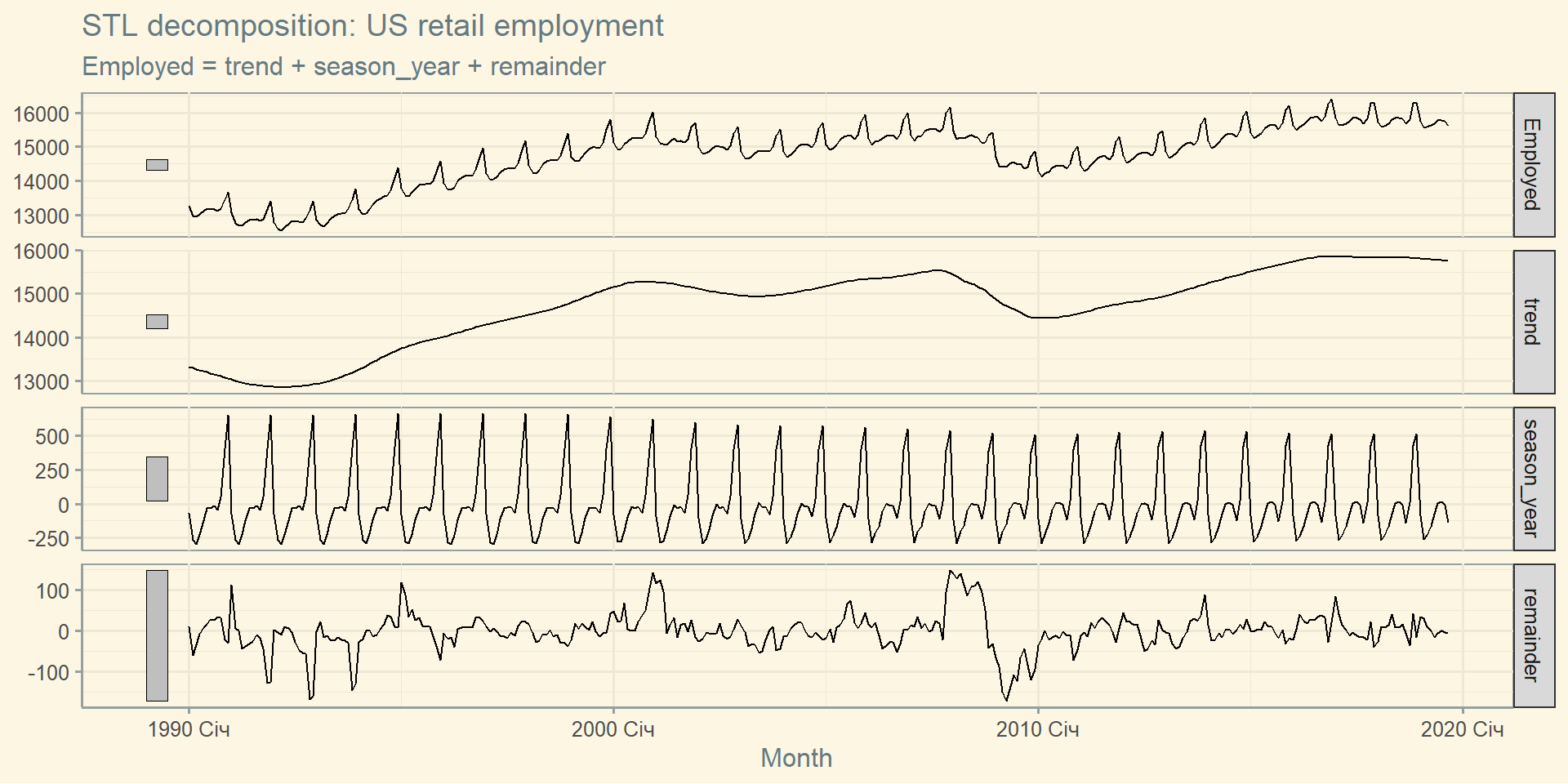
STL декомпозиція
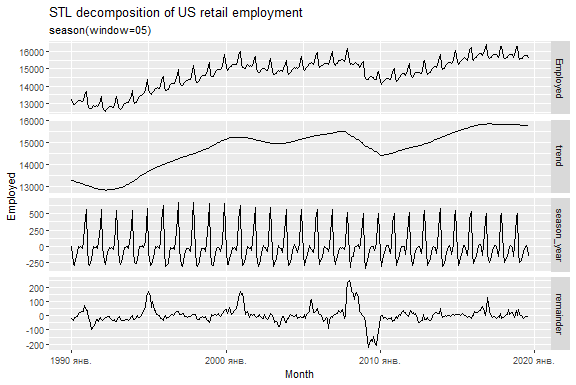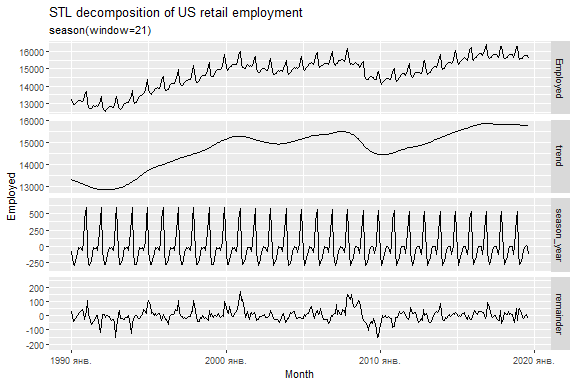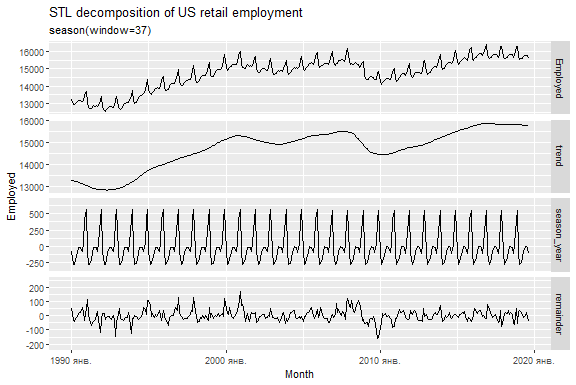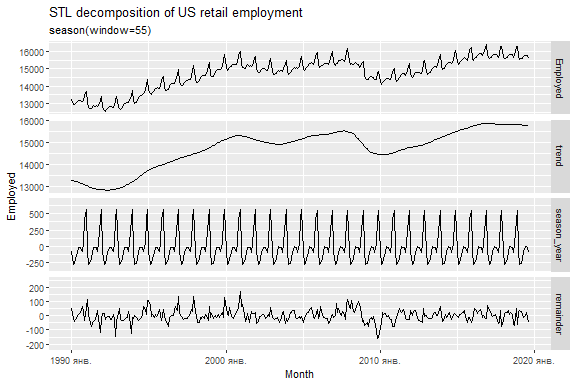
STL декомпозиція
# A dable: 357 x 7 [1M]
# Key: .model [1]
# : Employed = trend + season_year + remainder
.model Month Emplo…¹ trend seaso…² remai…³ seaso…⁴
<chr> <mth> <dbl> <dbl> <dbl> <dbl> <dbl>
1 STL(Employed ~ season(window… 1990 Січ 13256. 13294. -2.16 -36.2 13258.
2 STL(Employed ~ season(window… 1990 Лют 12966. 13273. -260. -47.3 13226.
3 STL(Employed ~ season(window… 1990 Бер 12938. 13252. -289. -25.1 13227.
4 STL(Employed ~ season(window… 1990 Кві 13012. 13231. -221. 2.25 13233.
5 STL(Employed ~ season(window… 1990 Тра 13108. 13209. -111. 9.96 13219.
6 STL(Employed ~ season(window… 1990 Чер 13183. 13188. -18.8 14.1 13202.
7 STL(Employed ~ season(window… 1990 Лип 13170. 13166. -17.9 22.1 13188.
8 STL(Employed ~ season(window… 1990 Сер 13160. 13144. -2.53 18.1 13162.
9 STL(Employed ~ season(window… 1990 Вер 13113. 13122. -34.0 25.3 13147.
10 STL(Employed ~ season(window… 1990 Жов 13185. 13100. 54.3 30.7 13131.
# … with 347 more rows, and abbreviated variable names ¹Employed, ²season_year,
# ³remainder, ⁴season_adjustus_retail_employment %>%
model(STL(Employed ~ trend(window=15) +
season(window="periodic"),
robust = TRUE)
) %>% components()# A dable: 357 x 7 [1M]
# Key: .model [1]
# : Employed = trend + season_year + remainder
.model Month Emplo…¹ trend seaso…² remai…³ seaso…⁴
<chr> <mth> <dbl> <dbl> <dbl> <dbl> <dbl>
1 "STL(Employed ~ trend(window… 1990 Січ 13256. 13247. -80.8 89.9 13337.
2 "STL(Employed ~ trend(window… 1990 Лют 12966. 13235. -273. 4.72 13240.
3 "STL(Employed ~ trend(window… 1990 Бер 12938. 13223. -258. -26.5 13197.
4 "STL(Employed ~ trend(window… 1990 Кві 13012. 13211. -186. -12.6 13198.
5 "STL(Employed ~ trend(window… 1990 Тра 13108. 13198. -88.4 -1.74 13197.
6 "STL(Employed ~ trend(window… 1990 Чер 13183. 13186. -8.47 5.67 13191.
7 "STL(Employed ~ trend(window… 1990 Лип 13170. 13173. -10.9 8.17 13181.
8 "STL(Employed ~ trend(window… 1990 Сер 13160. 13157. -11.5 13.5 13171.
9 "STL(Employed ~ trend(window… 1990 Вер 13113. 13142. -88.0 59.2 13201.
10 "STL(Employed ~ trend(window… 1990 Жов 13185. 13116. 39.0 29.8 13146.
# … with 347 more rows, and abbreviated variable names ¹Employed, ²season_year,
# ³remainder, ⁴season_adjusttrend(window = ?)контролює змінність тренду.season(window = ?)контролює зміну сезонної складової.season(window = 'periodic')еквівалентно нескінченному вікну.
STL декомпозиція
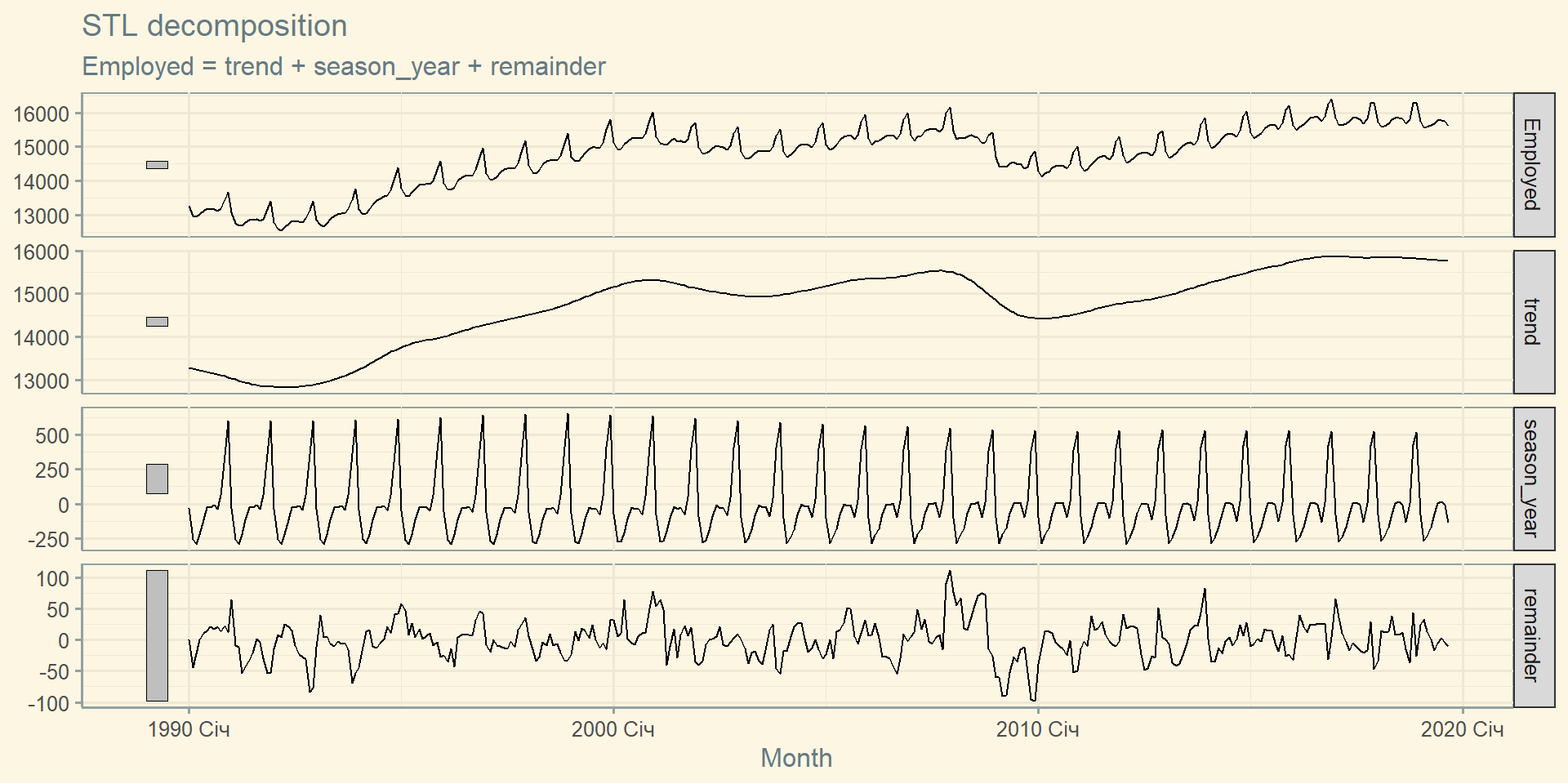
STL декомпозиція
Алгоритм, який ітеративно оновлює тренд та сезонність.
Починається з \(\hat{T}_t=0\)
Використовує суміш loess та ковзних середніх для послідовного уточнення тренду та сезонних оцінок.
Вікно тренду контролює пропускну здатність, що застосовується до десезоналізованих значень.
Сезонне вікно контролює пропускну здатність, що використовується для підсерії без тренду.
Вікно сезону за замовчуванням = 13
Дякую за увагу!
ihor.miroshnychenko@kneu.ua