02 - Порівняння середніх: t-розподіл

Кількісні методи в економіці

Ігор Мірошниченко

КНЕУ::ІІТЕ

оновлено: 2022-10-02

t-розподіл

Одновибірковий t-тест

Ми не знаємо стандартного відхилення в генеральній сукупності!

Ми оцінюємо стандартне відхилення в ГС на основі стандартного відхилення вибірки. В таких випадках тестова статистика розподілена не нормально, а за t-розподілом (Стьюдента).

\[t = \frac{\overline{x} - \mu} {s_x / \sqrt{N}}\]

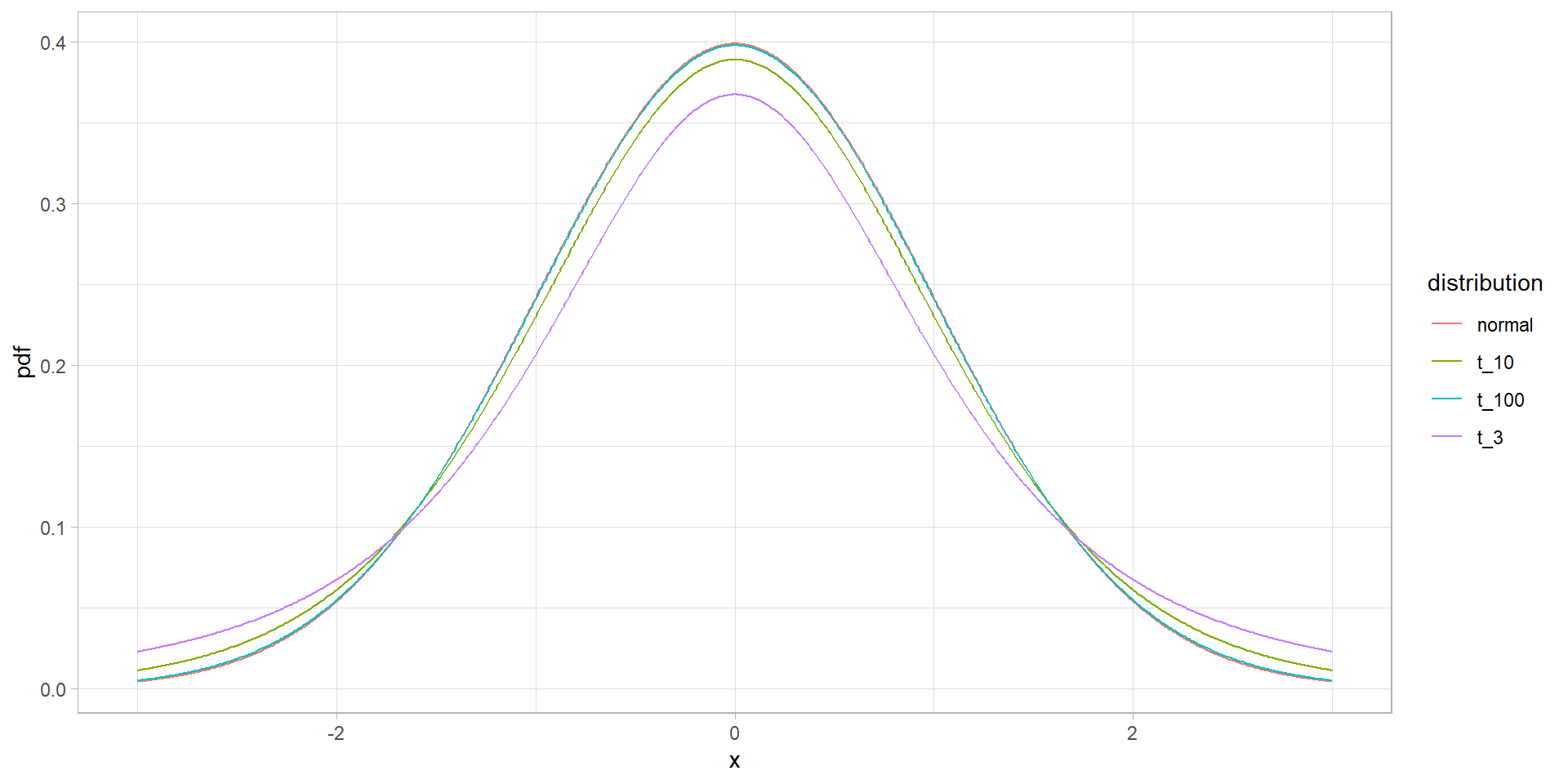
Форма цього розподілу дуже схожа на форму нормального розподілу, але має більш важкі “хвости” розподілу.

При ступеняха свободи k → ∞, розподіл Стьюдента дуже схоже на нормальний розподіл. І поріг при якому його приймають схожим буде при k ~ 30. Але що таке ступінь свободи розподілу?

Припустимо ми знаємо, чому дорівнює вибіркове середнє, тоді нам необхідно знати тільки \(n-1\) елементів вибірки, щоб безпомилково визначити чому дорівнює останній \(n\) елемент. Це не зовсім пояснює природу походження ступеня свободи, але дає алгоритм його знаходження.

t-розподіл

tibble(x = seq(-3, 3, .01),
       t_3 = dt(x, df = 3),
       t_10 = dt(x, df = 10),
       t_100 = dt(x, df = 100),
       normal = dnorm(x)) %>%
  pivot_longer(cols = -x, values_to = 'pdf', names_to = 'distribution') %>%
  ggplot(aes(x = x, y = pdf, colour = distribution))+
  geom_line()+
  theme_light()

Приклад

Порахуємо t-статистику на симульованих даних:

set.seed(2022)
samp <- rnorm(100, 100, 15)
m <- mean(samp)
sem <- sd(samp)/sqrt(length(samp))
t <- (m - 100)/sem
t

[1] 1.360131

І порівняємо з z-статистикою:

(m - 100) / (15/sqrt(100))

[1] 1.38746

Приклад

Порахуємо все одразу

t.test(samp, mu = 100)


    One Sample t-test

data:  samp
t = 1.3601, df = 99, p-value = 0.1769
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  99.04506 105.11732
sample estimates:
mean of x 
 102.0812

p-value

(1 - pt(t, df = length(samp) - 1))*2

[1] 0.1768777

Розберемо формулу

\[t = \frac{\overline{x} - \mu} {s_x / \sqrt{N}}\]

\(s_x / \sqrt{N}\) - це стандартна похибка середнього, тобто стандартне відхилення вибіркових середніх.
\(\sqrt{N}\): чим більша вибірки тим точніша наша вибірка, але зв’язок нелінійний. Тобто на малих вибірках додаткові спостереження дають значно більший приріст точності, ніж додаткові спостереження на великих вибірках.
\(s_x\): дисперсія вибірки. Чим більша дисперсія, тим більше значень нам потрібно для досягнення точності ГС. Чим менша дисперсія, тим менша стандартна похибка середнього.
\(s_x = \sqrt{\frac{\sum(x_i - \overline{x})^2}{n-1}}\). Чому в знаменнику \(n-1\)? Якби ми рахували дисперсію не від вибіркового середнього, а від середнього ГС, то дисперсія була б зі зміщенням. Тому для отримання незміщеної оцінки дисперсії необхідно ділити на \(n-1\).

Khan Academy

Порівняння середніх вибірок

t-тест

Є два різновиди t-тесту: залежний t-тест і незалежний t-тест.

Залежні тести припускають, що кожному значенню в одній вибірці ми можемо поставити відповідне значення з іншої вибірки. Зазвичай це повторні вимірювання якої-небудь ознаки в різні моменти часу.

У незалежних тестах немає можливості співстави одне значення з іншим. Ми вже не можемо безпосередньо співвіднести значення в двох вибірках один з одним, більш того, розмір двох вибірок може бути різним!

Залежний t-тест	Незалежний t-тест
`t.test(..., paired = TRUE)`	`t.test(..., paired = FALSE)`

Порівняння середніх вибірок

t-тест

Розглянемо задачу: > При порівнянні доходу двох груп отримали наступні результати:

	\(\overline{x}\)	\(sd_x\)	\(n\)
Група 1	89.9	11.3	20
Група 2	80.7	11.7	20

Ми хочемо дізнатися чи відрізняється дохід у цих двох груп. Для цього використаємо t-тест.

Нульова гіпотеза буде говорити про те, дохід від групи не залежить і середній дохід досліджуваних груп однаковий. Альтерантивна гіпотеза буде говорити про те, що дохід в групах різний.

Порівняння середніх вибірок

t-тест

Якби була вірна нульова гіпотеза, то це б означало, що обидві вибірки належать до однієї ГС.

Тому, якщо ми будемо багато разів повторювати наступний експеримент: беремо навмання дві вибірки з однієї з тієї ж ГС і рахуємо різницю середніх значень цих вибірок, то ми отримаємо нормальний розподіл різниць середніх значень навмання взятих вибірок з однієї і тієї ж ГС з параметрами нормального розподілу:

\[M = 0\]

\[D = se^2\]

Однак, ми вже з’ясували, що насправді ми отримуємо не нормально-розподілену величину, а величину, розподілену за розподілом Стьюдента з деяким параметром ступеня свободи \(df\).

Порівняння середніх вибірок

t-тест

Розрахунок параметрів розподілу Стьюдента

Стандарта похибка:

\[se=\sqrt{\frac{sd^2_1}{n_1} + \frac{sd^2_2}{n_2}}=\sqrt{\frac{11.3^2}{20} + \frac{11.7^2}{20}}\]

Тобто стандартна похибка середнього буде розраховуватися через знання стандартних відхилень вибірок і кількості елементів в них.

t-критерий:

\[t = \frac{(\bar{x_1} - \bar{x_2})+(M_{група\,1} - M_{група\,2})}{se} = \frac{(89.9 -80.7)}{\sqrt{\frac{11.3^2}{20} + \frac{11.7^2}{20}}} \approx 2.5\]

За підсумком ми отримали, що t-критерій дорівнює ~ 2.5. Це означає, що різниця між вибірковими середніми відхилилася на 2.5σ від вибіркового середнього рівного 0.

Порівняння середніх вибірок

t-тест

За допомогою калькулятора дізнаємося відсоток потраплять в область, коли відхилення досягають більше \(2.5σ\).

Для цього в калькуляторі виберемо t-розподіл з параметром \(df = df_1 + df_2 = n_1 - 1 + n_2 -1 = n_1 + n_2 -2 = 38\)
Зазначимо межі розподілу: ліва -2.5 і права 2.5
Отримаємо p-value = 0.016
Висновок:

Отримане p-value = 0.016 менше порога відхилення нульової гіпотези p-value <0.05. Значить, ми можемо сміливо відхиляти нульову гіпотезу і говорити про те, що дані вибірки належать різним генеральним сукупність, а отже дохід у цих груп різний

Замість калькулятора можна використовувати табличні значення t-розподілу.

t-тест

Порівняння середніх вибірок: візуалізація Порівняння середніх вибірок: візуалізація

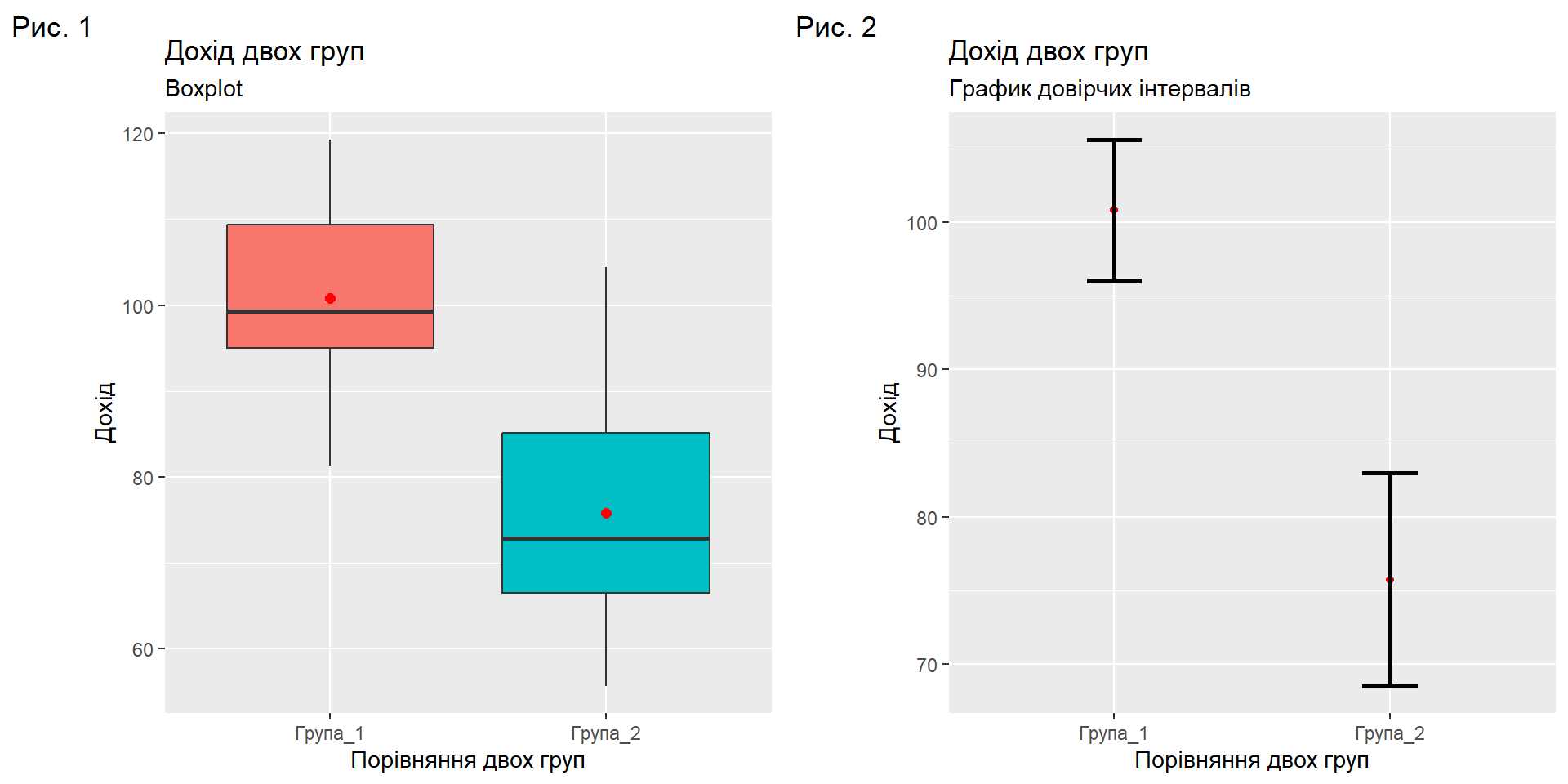
Порівняння середніх вибірок

t.test(df$Група_1, df$Група_2, var.equal = TRUE)


    Two Sample t-test

data:  df$Група_1 and df$Група_2
t = 6.0478, df = 38, p-value = 4.895e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 16.68494 33.47506
sample estimates:
mean of x mean of y 
  100.815    75.735

Припущення

Припущення 1: нормальність

Щоб p-value був коректним, деякі допущення повинні бути виконані:

Нормальність розподілу. Це найвідоміше допущення, але напевно найменш важливе. Існує твердження, що вибірки повинні бути взяті з нормального розподілу. Це не зовсім так: так, вірно, це достатня умова, але не необхідне. В першу чергу, важливо саме вибіркове розподіл (середніх різниць або різниць середніх), яке досягається за рахунок центральної граничної теореми особливо при великій вибірці. Звідси і всі правила в дусі “для t-тесту розподіл має бути нормальним, але якщо n> 30, то це не обов’язково.” Звідки саме 30? Так нізвідки, просто. Як і з усіма точними числами в статистиці.

Для перевірки на нормальність окрім QQ-plot існують статистичні тести, наприклад тест Шапіро-Уілка shapiro.test()

Припущення 1: нормальність

shapiro.test(df$Група_1)


    Shapiro-Wilk normality test

data:  df$Група_1
W = 0.96342, p-value = 0.6142

У нашому випадку p-value більше 0.05, що логічно: ми взяли цю вибірку саме з нормального розподілу.

Якщо p-value менше рівня α, який у нас стандартно 0.05, то ми можемо відкинути нульову гіпотезу про те, що вибірка взята з нормального розподілу. Якщо це так, то нам потрібно, по ідеї, відмовитися від t-тесту і використовувати непараметричний тест, який не має вимог до розподілу досліджуваної змінної.

Припущення 1: нормальність

Однак проведення тесту на нормальність для перевірки припущення про нормальність - річ досить безглузда.

Справа в тому, що тест Шапіро-Уілкі - це такий же статистичний тест, як і всі інші: чим більше вибірка, тим з більшою ймовірністю він “зловить” відхилення від нормальності, чим менше вибірка, тим з меншою ймовірністю він виявить навіть серйозні відхилення від нормальності.

А нам-то потрібно навпаки! При великій вибірці відхилення від нормальності нам не особливо страшні, а при маленькій тест все одно нічого не виявить.

Більш того, ідеально нормальних розподілів в природі взагалі майже не існує! А це означає, що при досить великій вибірці тест Шапіро-Уілкі практично завжди буде знаходити відхилення від нормальності. Все це робить його малоінформативною при тестуванні допущення про нормальність. Це ж вірно і для інших тестів на нормальність.

Припущення 2: гомогенність дисперсії

Для незалежного t-тесту вибірки повинні бути взяті з розподілу з однаковими дисперсіями. Однак це не так критично із застосуванням поправки Уелча.

Припущення 3: незалежність значень

Незалежність значень (або пар) у вибірці. Типовим прикладом порушення незалежності є випадок, коли t-тест застосовується на неусереднених значеннях.

Непараметричні аналоги t-тесту

Якщо вибірка не дуже велика і взята з сильно асиметричного розподілу або вибірка представляє собою порядкові дані, то можна скористатися непараметричних альтернативами для t-тесту.

Непараметричні тести не мають припущень про розподіл, що робить їх більш універсальними. Більшість подібних тестів передбачають перетворення даних в ранги, тобто всередині цих тестів відбувається перетворення в рангову шкалу. Таке перетворення може знизити статистичну потужність тесту і привести до підвищення ймовірності помилки другого роду.

Непараметричні аналоги t-тесту

Тест Уилкоксона

Непараметричний аналог двостороннього залежного t-тесту називається тестом Уилкоксона. Функція для нього називається wilcox.test(), і вона має такий же синтаксис, як і t.test().

x <- c(1.83,  0.50,  1.62,  2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)
wilcox.test(x, y, paired = TRUE)


    Wilcoxon signed rank exact test

data:  x and y
V = 40, p-value = 0.03906
alternative hypothesis: true location shift is not equal to 0

Непараметричні аналоги t-тесту

Тест Манна-Уїтні

Непараметричним аналогом двостороннього незалежного t-тесту є тест Манна-Уїтні. Для нього теж використовується функція wilcox.test(), тільки в даному випадку з параметром paired = FALSE.

wilcox.test(x, y, paired = FALSE)


    Wilcoxon rank sum test with continuity correction

data:  x and y
W = 58, p-value = 0.1329
alternative hypothesis: true location shift is not equal to 0

Непараметричні аналоги t-тесту

Залежний t-тест:	Незалежний t-тест:
`t.test(..., paired = TRUE)`	`t.test(..., paired = FALSE)`
Тест Уилкоксона	Тест Манна-Уїтні
`wilcox.test(..., paired = TRUE)`	`wilcox.test(..., paired = FALSE)`

Приклад

library(tidyverse)
library(gapminder)

mean <- gapminder %>% 
  group_by(country) %>% 
  summarise(mean_life = mean(lifeExp)) %>% 
  expand_grid(mean_1 = .$mean_life, mean_2 = .$mean_life)

country <- gapminder %>% 
  group_by(country) %>% 
  summarise(mean_life = mean(lifeExp)) %>% 
  expand_grid(country_1 = .$country, country_2 = .$country)

Приклад

bind_cols(country1 = country$country_1, 
          mean1 = mean$mean_1, 
          country2 = country$country_2, 
          mean2 = mean$mean_2) %>% 
  mutate(diff = abs(mean1 - mean2)) %>% 
  filter(diff != 0) %>% 
  distinct() %>% 
  arrange(diff) %>% 
  slice(seq(1, nrow(.), by = 2))

# A tibble: 10,011 x 5
   country1         mean1 country2      mean2    diff
   <fct>            <dbl> <fct>         <dbl>   <dbl>
 1 Bolivia           52.5 Congo, Rep.    52.5 0.00267
 2 Eritrea           46.0 Zambia         46.0 0.00292
 3 Belgium           73.6 Israel         73.6 0.00408
 4 Costa Rica        70.2 Poland         70.2 0.00450
 5 Chad              46.8 Yemen, Rep.    46.8 0.00683
 6 Cambodia          47.9 Tanzania       47.9 0.00958
 7 Hong Kong, China  73.5 United States  73.5 0.0143 
 8 Congo, Dem. Rep.  44.5 Niger          44.6 0.0149 
 9 Nepal             49.0 Swaziland      49.0 0.0161 
10 Kenya             52.7 Zimbabwe       52.7 0.0178 
# ... with 10,001 more rows

Приклад

data <- gapminder %>% 
  filter(country %in% c("Eritrea", "Zambia")) 

t.test(data$gdpPercap ~ data$country)


    Welch Two Sample t-test

data:  data$gdpPercap by data$country
t = -9.4275, df = 19.492, p-value = 1.069e-08
alternative hypothesis: true difference in means between group Eritrea and group Zambia is not equal to 0
95 percent confidence interval:
 -998.3154 -636.0784
sample estimates:
mean in group Eritrea  mean in group Zambia 
             541.0025             1358.1994

Дякую за увагу!

ihor.miroshnychenko@kneu.ua