01 - Розвідувальний аналіз даних
Кількісні методи в економіці
Ігор Мірошниченко
КНЕУ::ІІТЕ
оновлено: 2022-09-30
Про мене
- Мірошниченко Ігор Вікторович
- кандидат економічних наук
- доцент кафедри математичного моделювання і статистики КНЕУ
- викладач Міжнародного інституту бізнесу (MBA)
ihor.miroshnychenko@kneu.ua
Типи даних
Типи даних
- Числові
- неперервні
- дискретні
- Категоріальні
- двійкові
- порядкові
Типи даних
Неперервні (continuous) - дані, які можуть приймати будь-які числові значення
Дискретні (discrete) - дані, які приймають тільки цілочисельні значення
Категоріальні (categorical) - дані, які набувають тільки окремих значень.
Бінарні / двійкові (binary) - дані лише з двома категоріями
Порядкові - дані з вираженою впорядкованістю
Міри центральної тенденції
Міри центральної тенденції
Середнє арифметичне
Сума всіх значень, що поділено на їх кількість.
\[\overline{x}=\frac{\sum_{i}^{n}x_i}{n}\]
Усічене середнє значення
Різновид середнього, яке обчислюється шляхом відкидання фіксованого числа відсортованих значень з кожного кінця послідовності і потім взяття середнього арифметичного решти значень
\[\overline{x} = \frac{\sum_{i=p+1}^{n-p}x_i}{n-2p}\]
p - кількість найбільших та найменших значень.
Середнє зважене
Надаємо різну вагу значенням
\[\overline{x_w} = \frac{\sum_{i}^{n}w_ix_i}{\sum_{i}^{n}w_i}\]
- Деякі значення більш мінливі ніж інші, і мінливим значенням надається більша вага. Наприклад, якщо один з датчиків менш точний, його вагу можна понизити.
- Зібрані дані не однаково репрезентують різні групи. Наприклад, надати більшу вагу групі даних, яких представлено менше.
Медіана та робасті оцінки
Медіана - це число, ділить впорядковану множену значень навпіл.
Якщо число даних парне, серединним значенням є те, що не знаходиться в наборі даних фактично, а є середнім арифметичним двох значень, які ділять впорядковані дані на верхню і нижню половини.
Медіану називають робастою оцінкою центрального положення, оскільки вона стійка до викидів.
Викиди - це спостереження, які сильно відрізняються від інших даних.
Міри центральної тенденції
| country | continent | year | lifeExp | pop | gdpPercap |
|---|---|---|---|---|---|
| Afghanistan | Asia | 1952 | 28.801 | 8425333 | 779.4453 |
| Afghanistan | Asia | 1957 | 30.332 | 9240934 | 820.8530 |
| Afghanistan | Asia | 1962 | 31.997 | 10267083 | 853.1007 |
| Afghanistan | Asia | 1967 | 34.020 | 11537966 | 836.1971 |
| Afghanistan | Asia | 1972 | 36.088 | 13079460 | 739.9811 |
| Afghanistan | Asia | 1977 | 38.438 | 14880372 | 786.1134 |
Міри центральної тенденції
Розрахуємо середнє, зважене середнє, усічене середнє та медіану для ВВП:
gapminder %>%
group_by(continent) %>%
summarise('середнє' = mean(gdpPercap),
'усічене середнє' = mean(gdpPercap, trim = 0.1),
'медіана' = median(gdpPercap)) %>%
knitr::kable()| continent | середнє | усічене середнє | медіана |
|---|---|---|---|
| Africa | 2193.755 | 1557.042 | 1192.138 |
| Americas | 7136.110 | 5823.602 | 5465.510 |
| Asia | 7902.150 | 4915.853 | 2646.787 |
| Europe | 14469.476 | 13532.972 | 12081.749 |
| Oceania | 18621.609 | 18059.966 | 17983.304 |
Міри центральної тенденції
Розрахуємо середньостатистичну кількість населення в країні, то повинні використовувати середнє зважене або медіану, щоб врахувати різну чисельність населення на кожному континенті.
gapminder %>%
group_by(continent) %>%
summarise('середнє' = mean(pop),
'зважене середнє' = weighted.mean(pop, w = lifeExp),
'медіана' = median(pop)) %>%
knitr::kable()| continent | середнє | зважене середнє | медіана |
|---|---|---|---|
| Africa | 9916003 | 10266549 | 4579311 |
| Americas | 24504795 | 26342188 | 6227510 |
| Asia | 77038722 | 78390133 | 14530831 |
| Europe | 17169765 | 17266114 | 8551125 |
| Oceania | 8874672 | 9013577 | 6403492 |
Мода
Значення ознаки, яке зустрічається максимально часто
Оцінки варіації
Оцінки варіації
Середнє абсолютне відхилення
Середнє абсолютних значень відхилень від середнього
\[MAE = \frac{\sum_{i=1}^{n}|x_i - \overline{x}|}{n}\]
Дисперсія
Сума квадратичних відхилень від середнього, поділена на \(n - 1\), де \(n\) - кількість даних
\[S^2 = \frac{\sum{(x - \overline{x})^2}}{n-1}\]
Стандартне відхилення
Квадратний корінь з дисперсії
\[S = \sqrt{S^2}\]
Оцінки варіації
Медіанне абсолютне відхилення від медіани (median absolute deviation, MAD)
Робаста оцінка варіабельності
\[MAD = median(|x_1 - m|, |x_2 - m|, ...,|x_N - m|)\]
m - медіана.
Розмах (range)
Різниця між найбільшим і найменшим значеннями в наборі даних
\[Range = max(x_i)-min(x_i)\]
Оцінки варіації
Процентиль (percentile)
Для того щоб запобігти чутливість до викидів, можна звернутися до розмаху даних після відкидання значень з кожного кінця. Ці типи оцінок формально грунтуються на різниці між процентилями.
У наборі даних P-й процентиль є таким значенням, що P відсотків значень приймає це значення або менше і (100 - P) відсотків значень приймає це значення або більше.
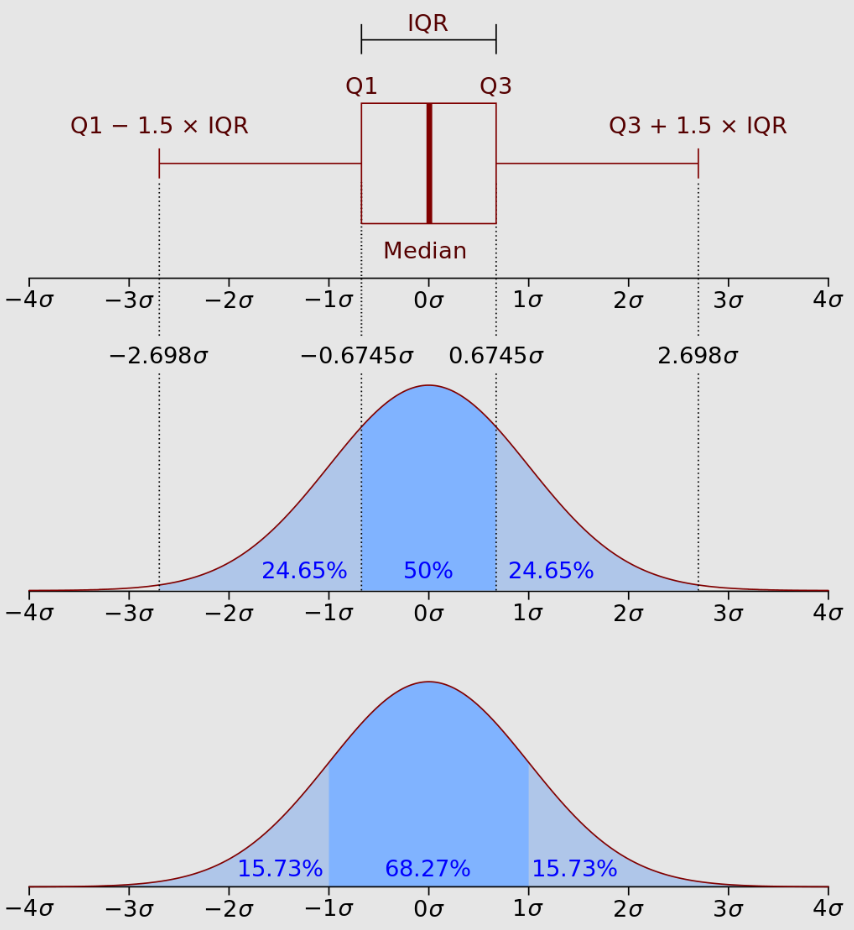
Міжквартальний розмах (IQR)
Різниця між 75-м і 25-м процентилями
Загальний перелік:
- Квантиль (quantile) - 3 рівні частини
- Квартиль (quartile) - 4 рівні частини
- Квінтіль (quintile) - 5 рівних частин
- Дециль (deciles) - 10 рівних частин
- Перцентиль (percentile) - 100 рівних частин
Оцінки варіації
| country | continent | year | lifeExp | pop | gdpPercap |
|---|---|---|---|---|---|
| Afghanistan | Asia | 1952 | 28.801 | 8425333 | 779.4453 |
| Afghanistan | Asia | 1957 | 30.332 | 9240934 | 820.8530 |
| Afghanistan | Asia | 1962 | 31.997 | 10267083 | 853.1007 |
| Afghanistan | Asia | 1967 | 34.020 | 11537966 | 836.1971 |
| Afghanistan | Asia | 1972 | 36.088 | 13079460 | 739.9811 |
| Afghanistan | Asia | 1977 | 38.438 | 14880372 | 786.1134 |
Процентилі рівня ВВП на душу населення
Основні статистичні візуалізації
Точкова діаграма
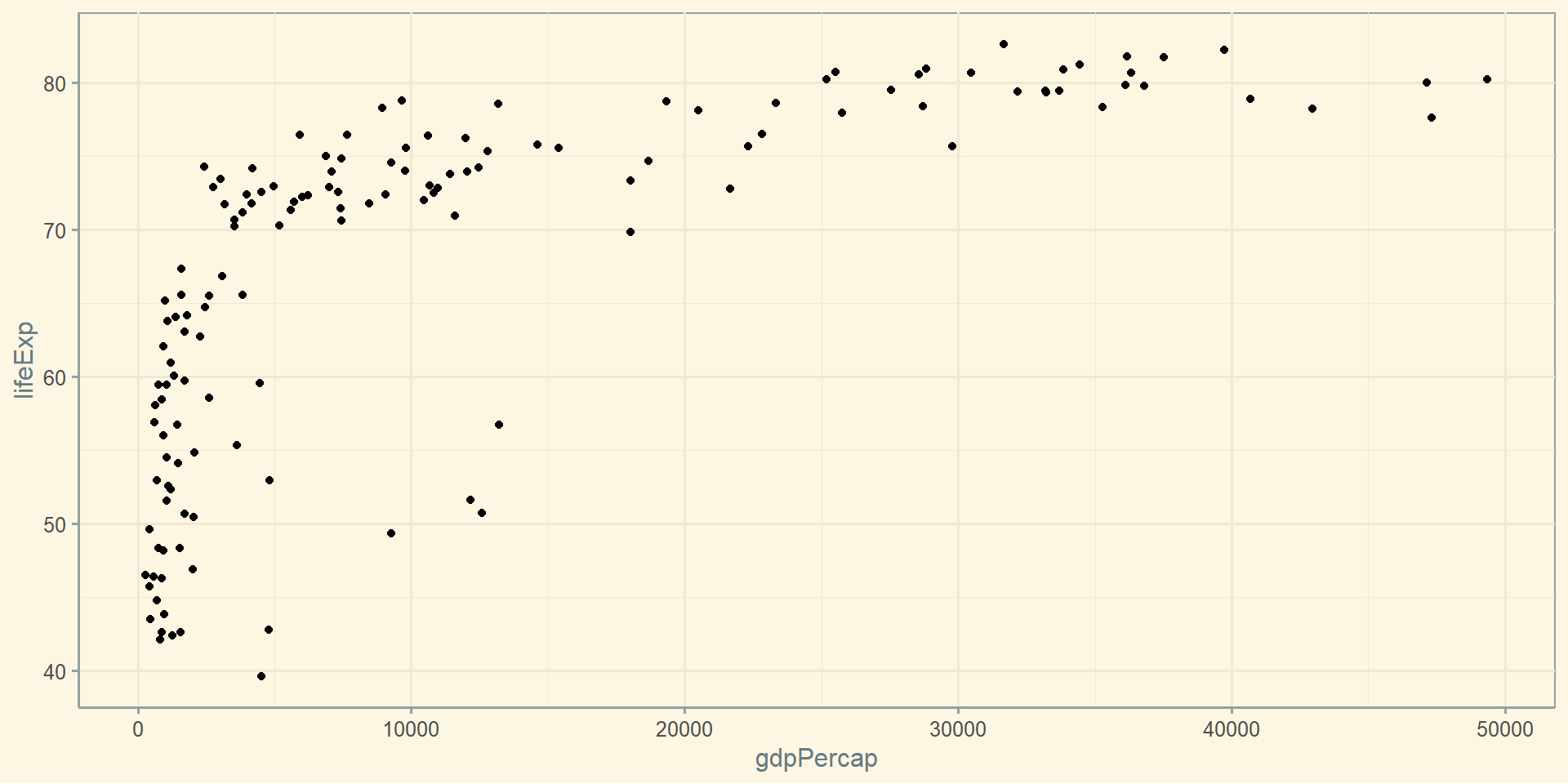
Точкова діаграма
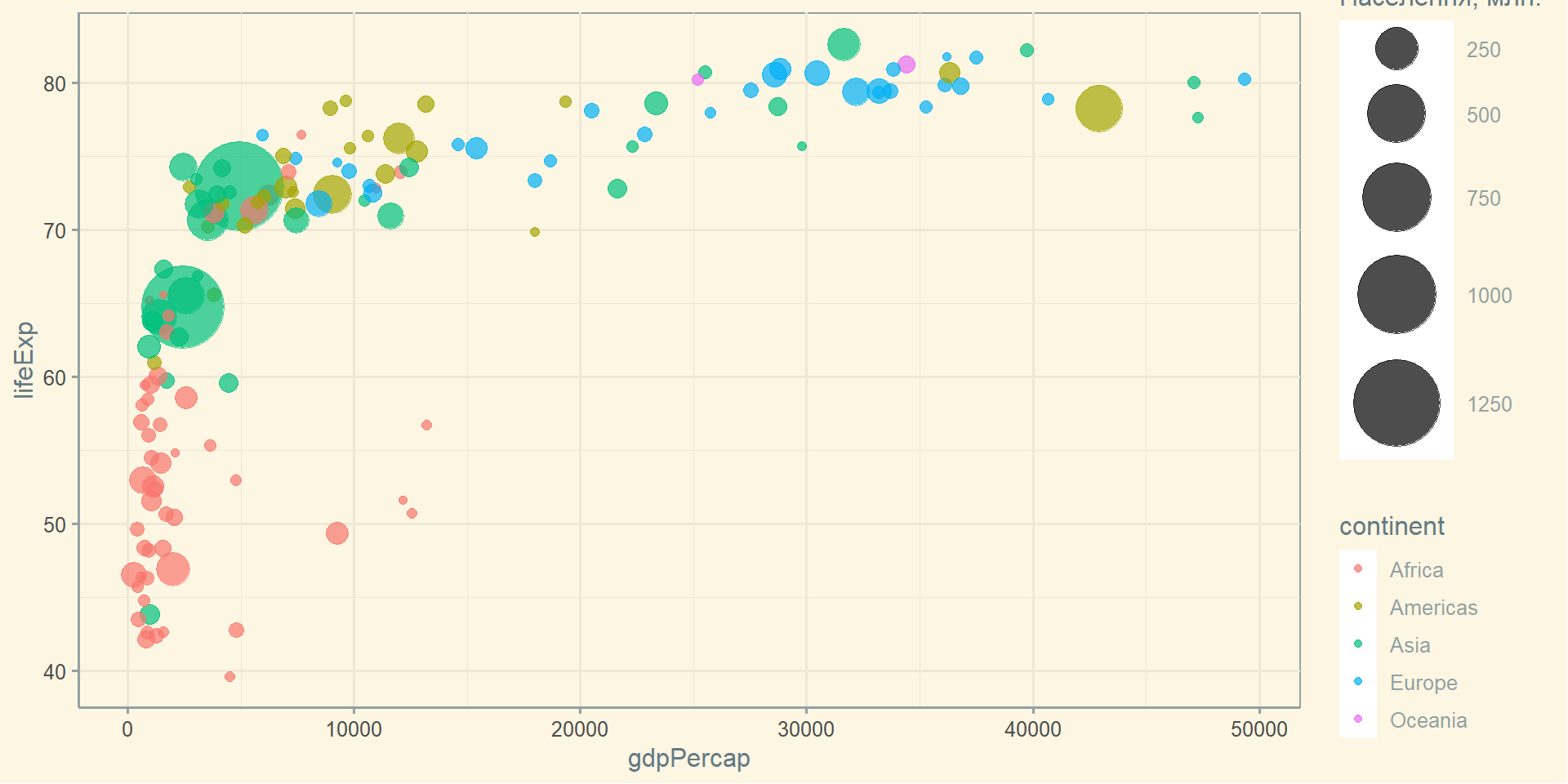
Box-plot
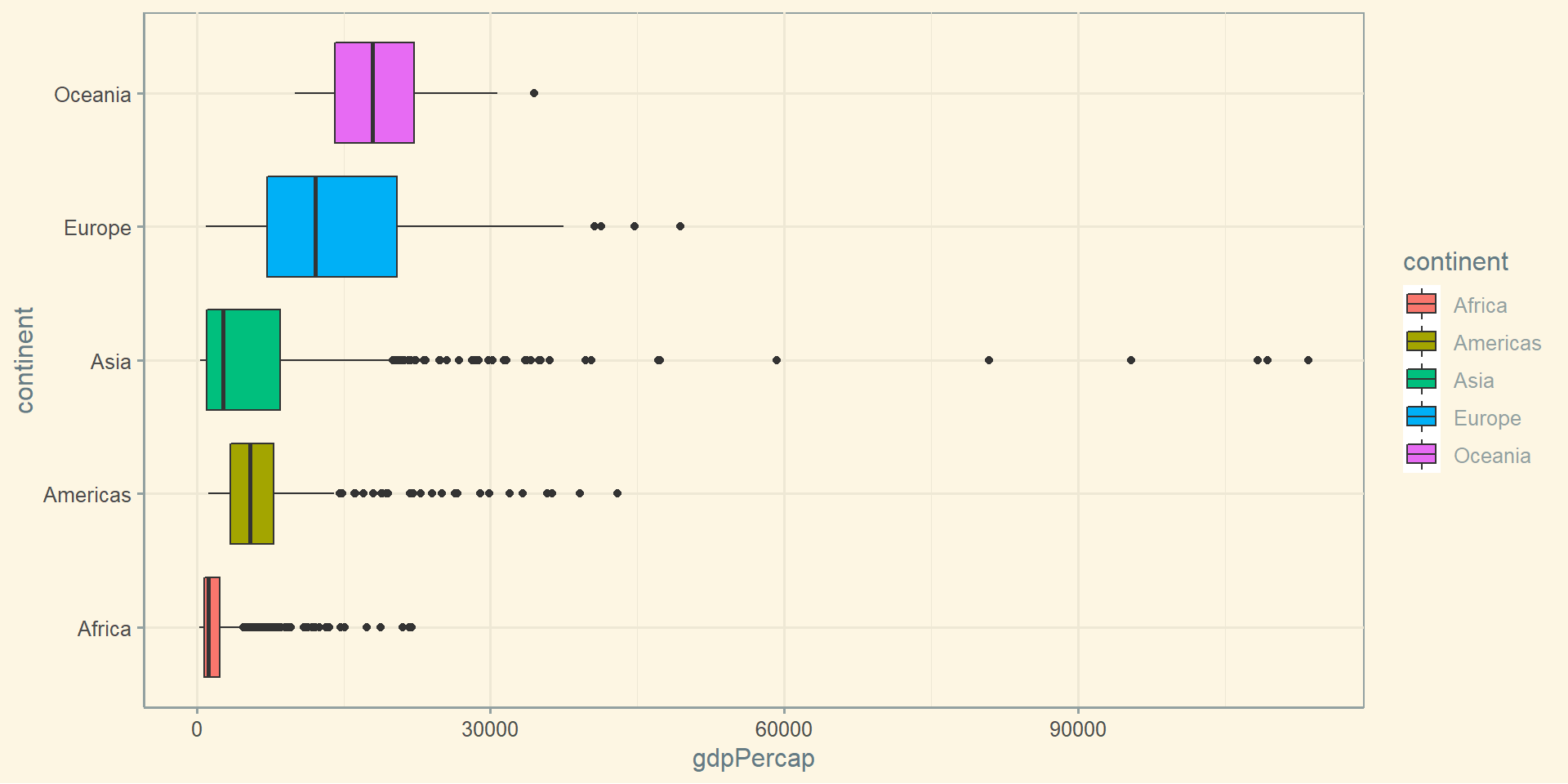
Скрипічний графік
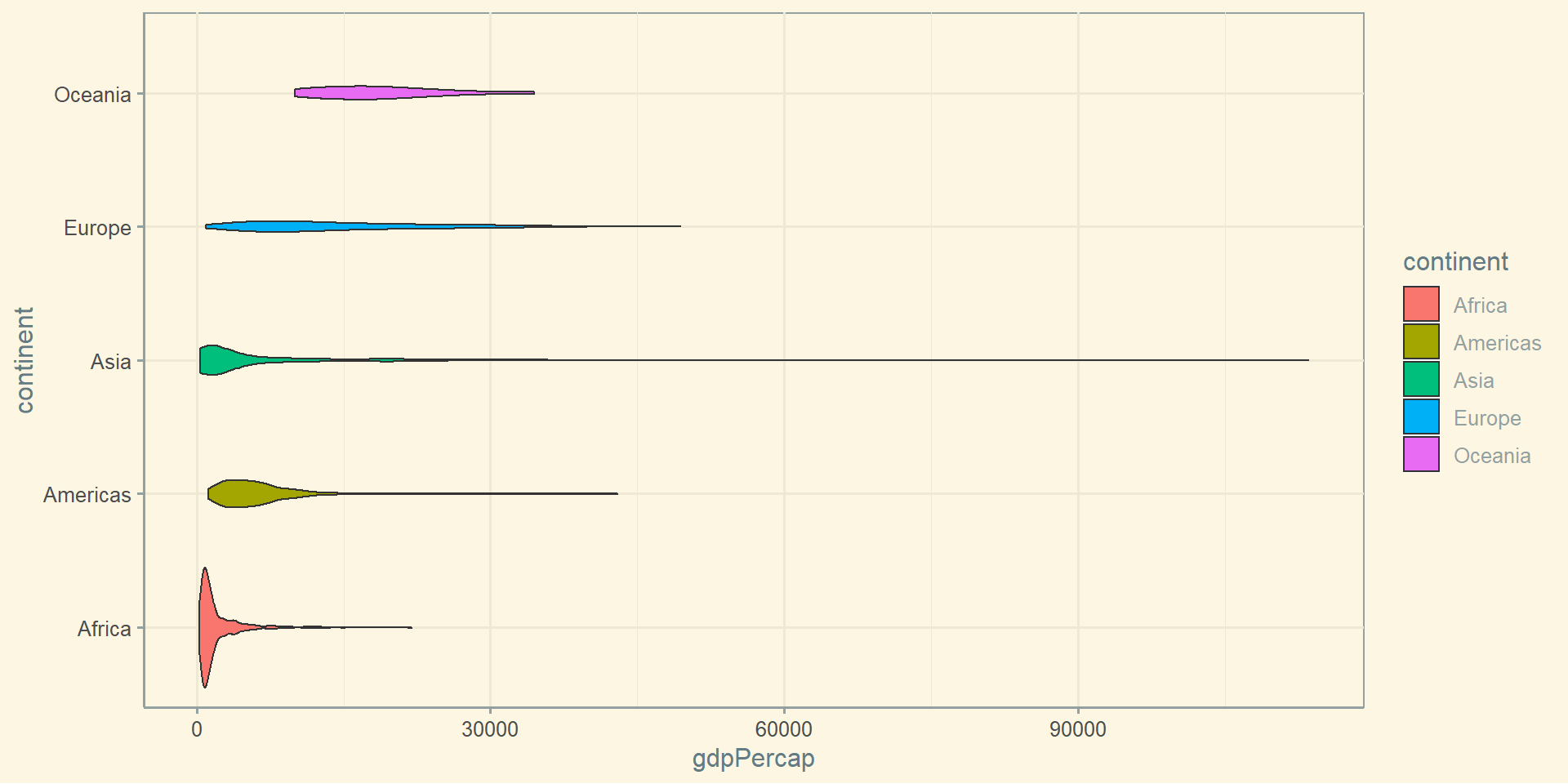
Гістограма
Графік, який показує як часто значення змінної зустрічається на певному проміжку
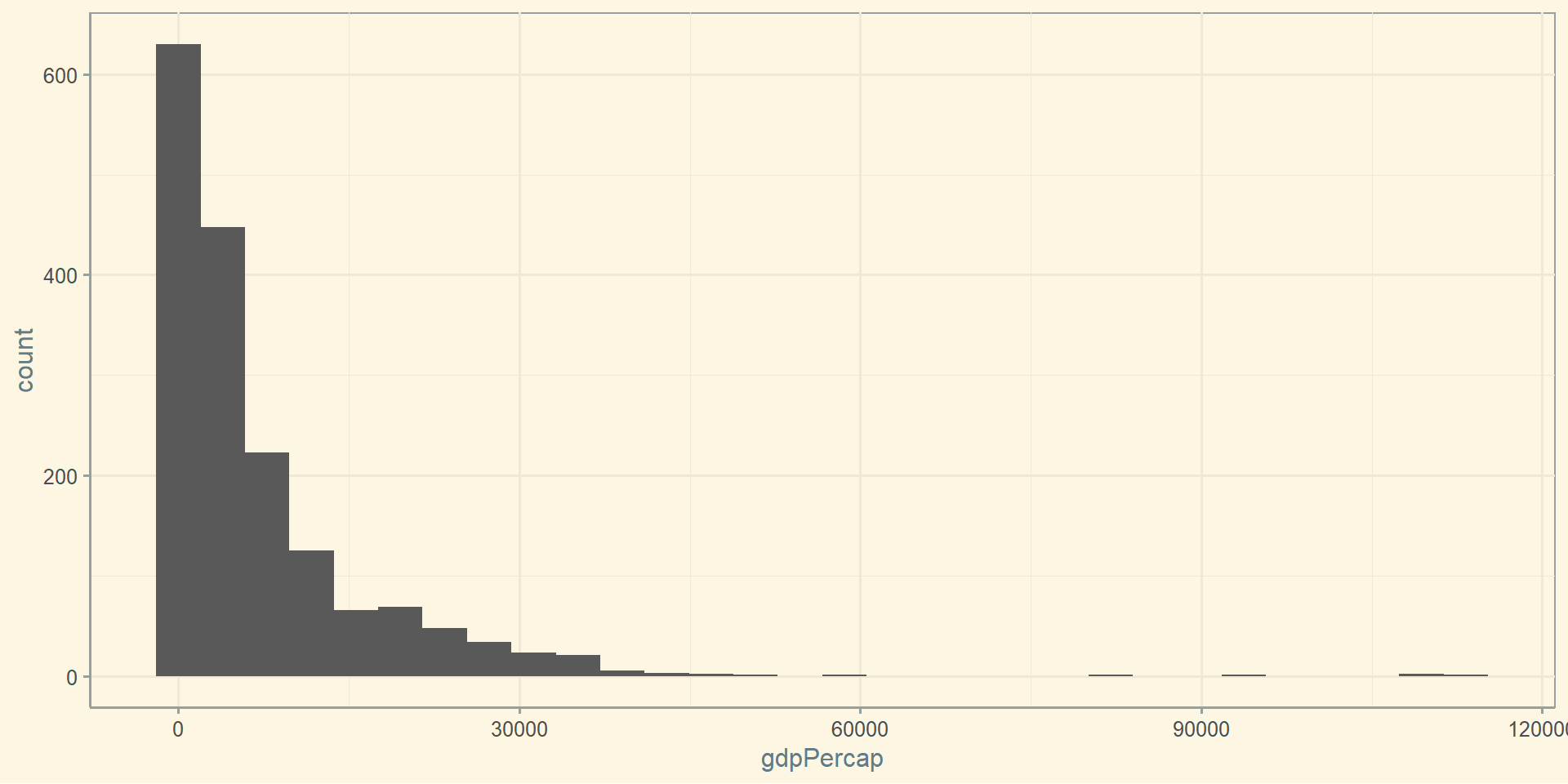
Графік щільності розподілу
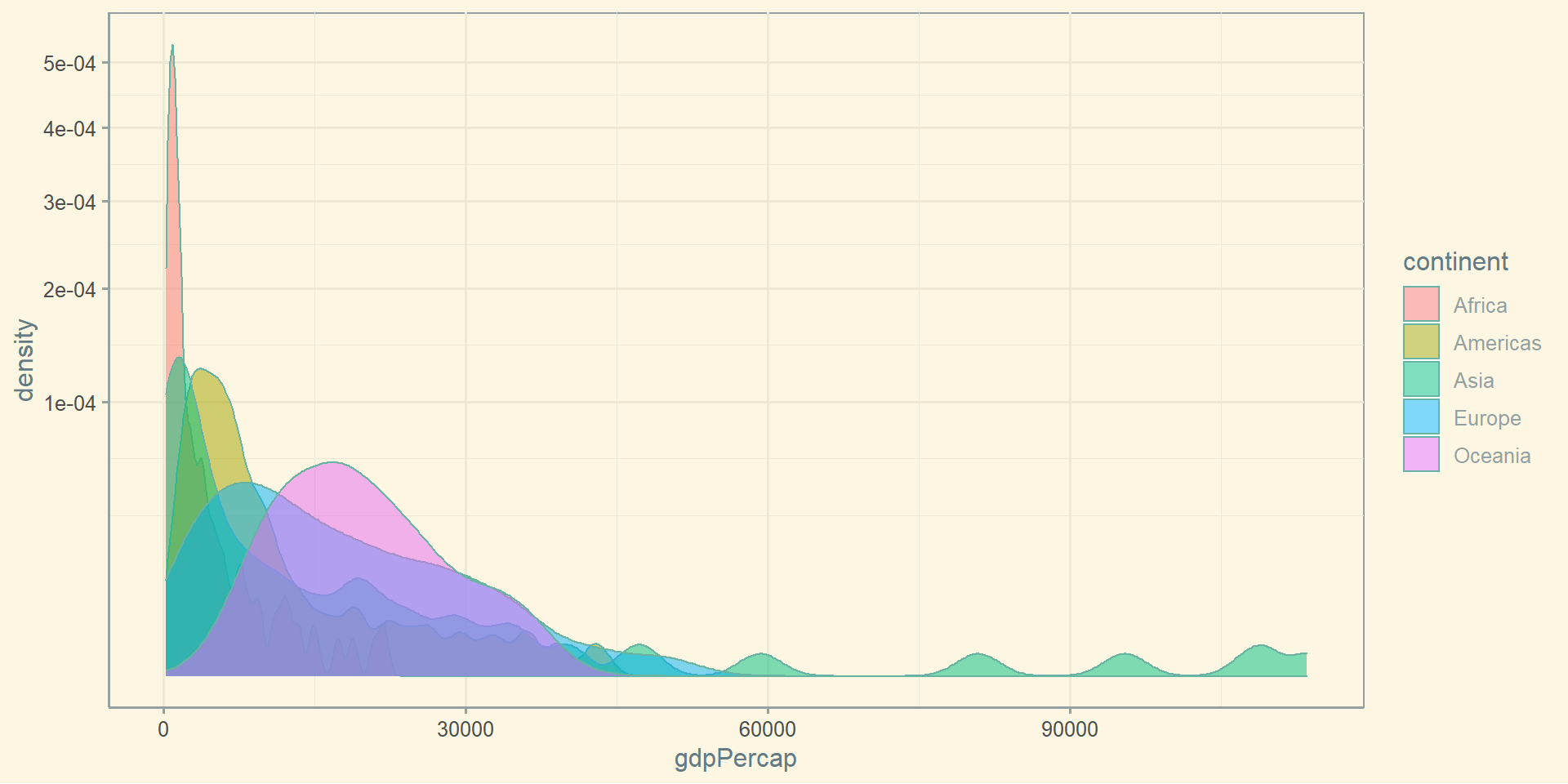
Стовпчаста діаграма
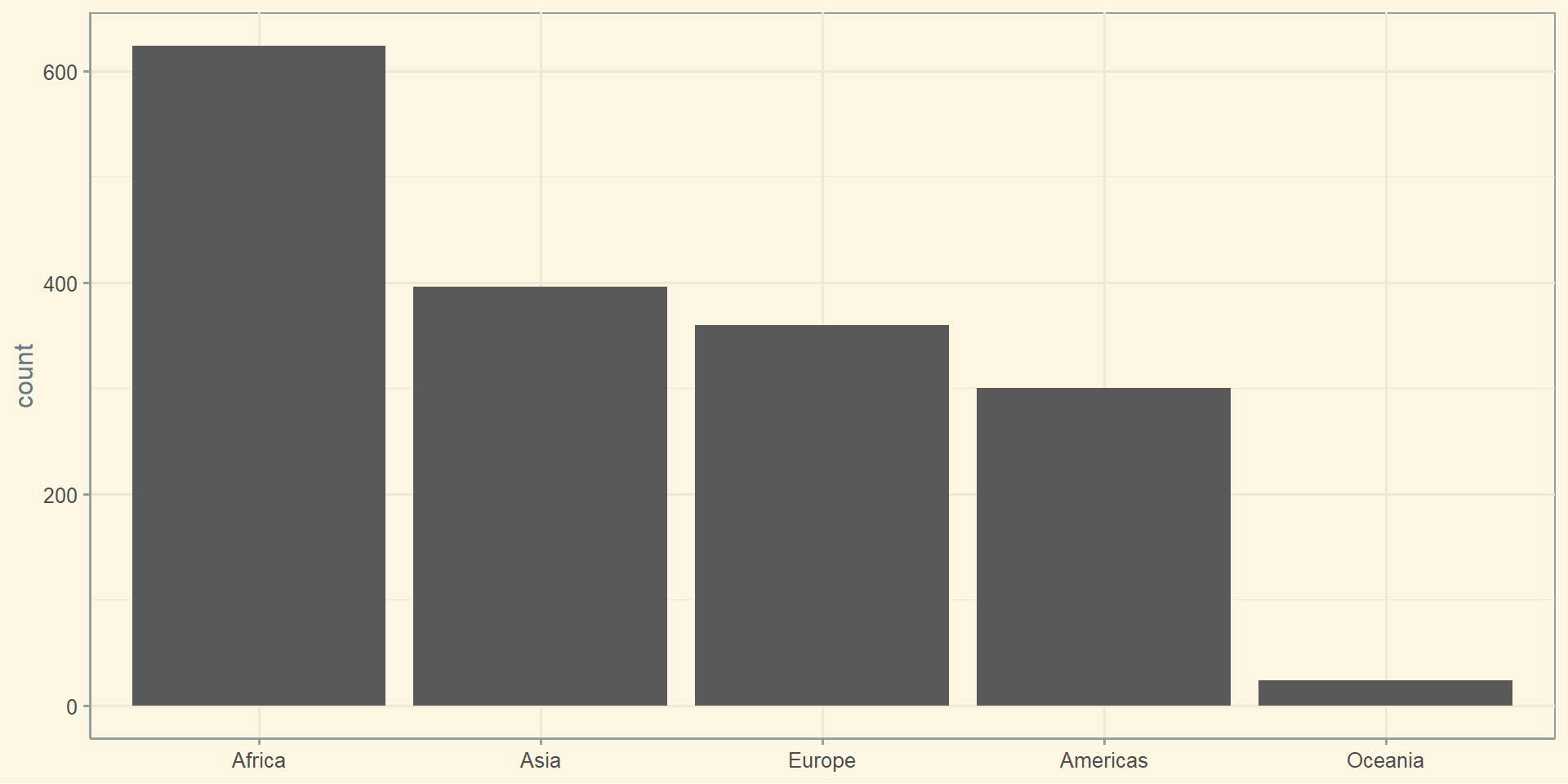
Кореляційна матриця
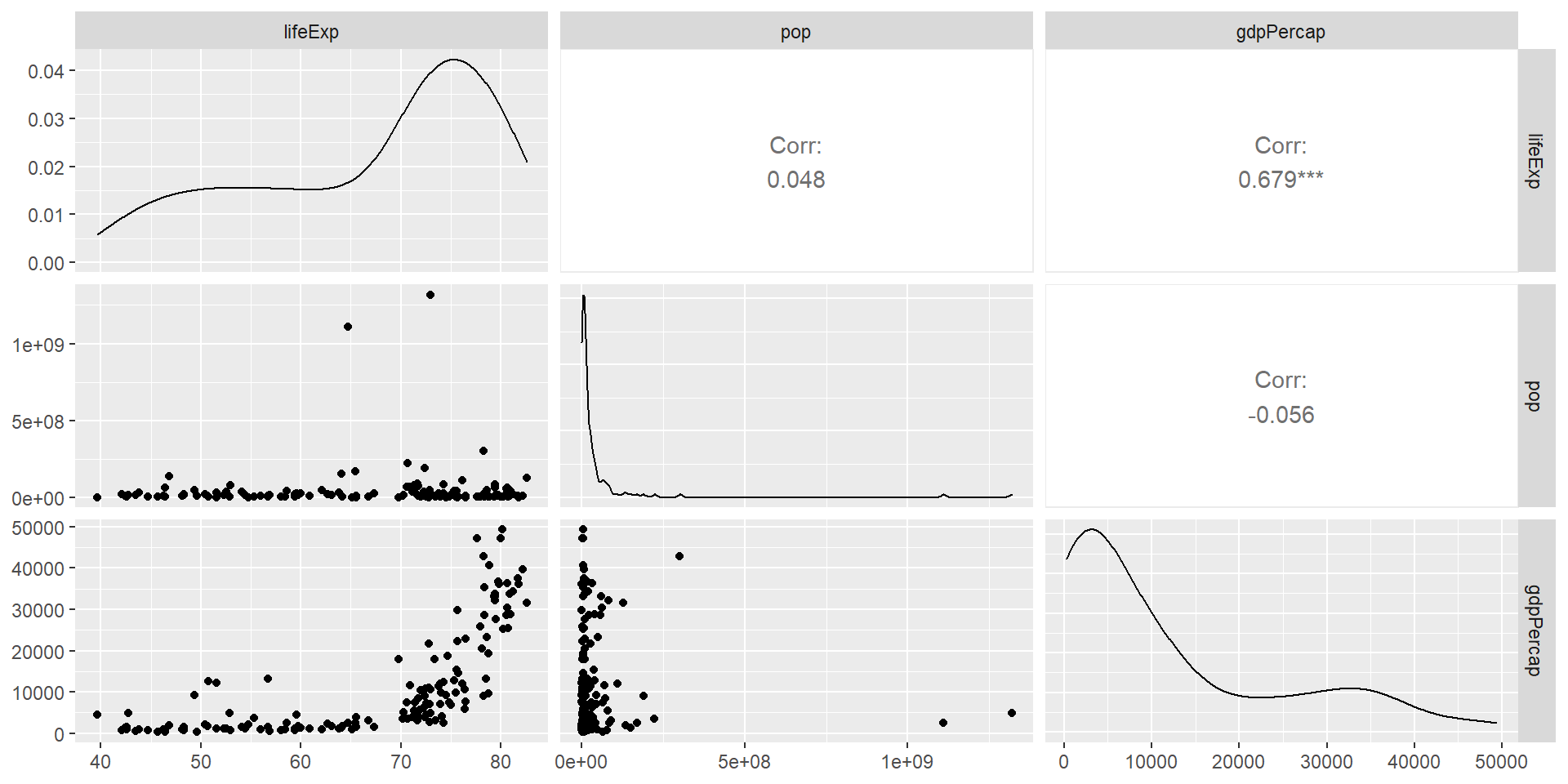
Кореляційна матриця
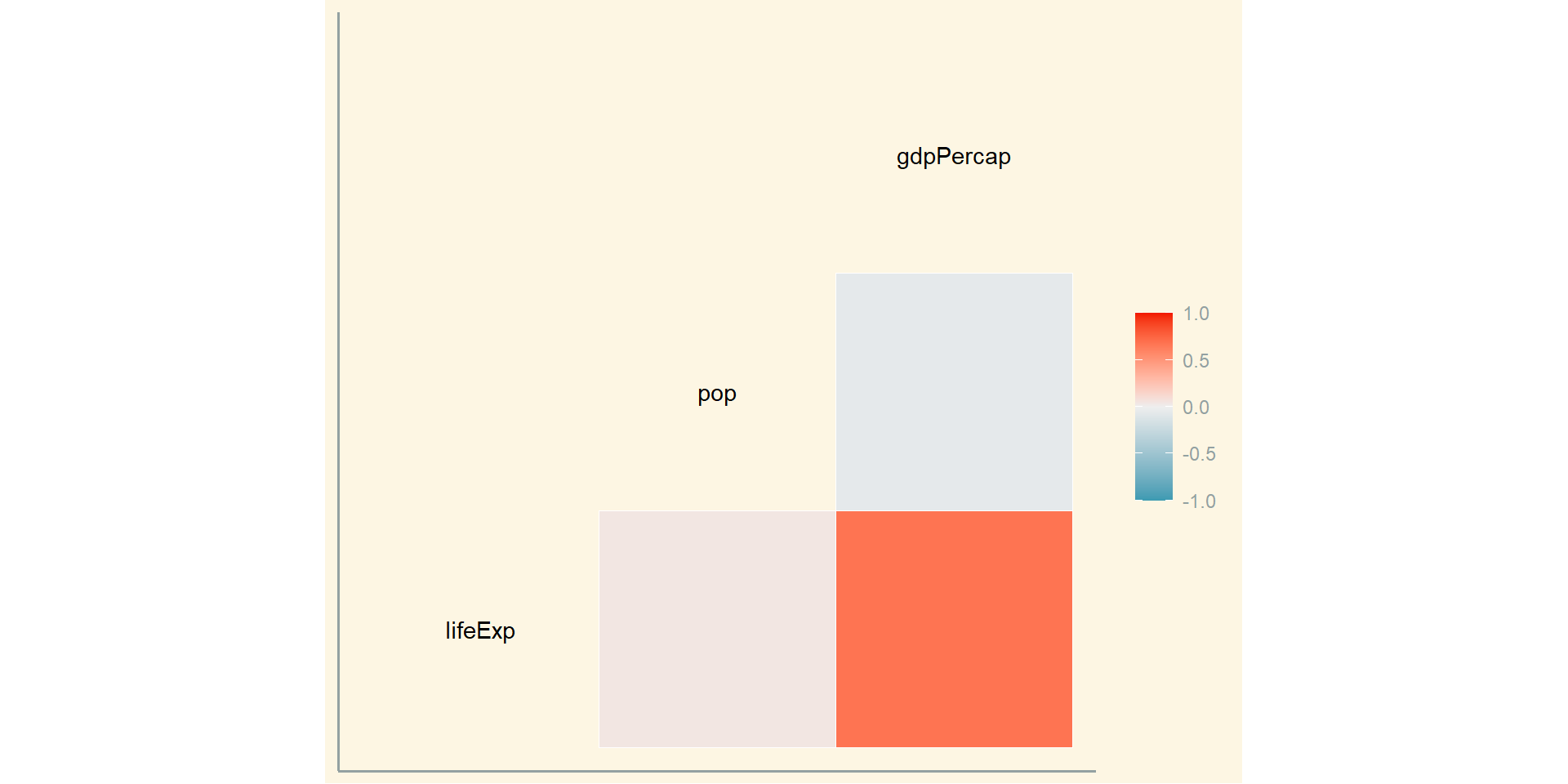
Вибірки даних
Вибірки даних
Генеральна сукупність
Множина всіх об’єктів, щодо яких робляться висновки в рамках дослідження.
Вибірка
Частина генеральної сукупності, яка охоплюється експериментом.

Типи вибірок
Проста випадкова (simple random sample) - вибірка, що отримується в результаті випадкового відбору без розбивки на страти.
- з поверненням
- без повернення
Стратифікована (stratified sampling) - поділ популяції на страти і випадковий відбір елементів з кожної страти
Групова вибірка (cluster sample) - члени популяції вибираються випадковим чином, з природних груп, що називаються «кластером».
Середнє вибірки vs. середнє генеральної сукупності
\(\overline{x}\) - форма запису для середнього вибірки.
\(\mu\) - форма запису для середнього генеральної сукупності
Властивості:
\(\mu = \frac{1}{n}\sum{x_i}\)
\(\sum{(x - \mu)} = 0\)
Умовні позначення
| Вибірка (sample) | Генеральна сукупність (population) | |
|---|---|---|
| Середнє (mean) | \(\overline{x}\) | \(\mu\) |
| Стандартне / середньоквадратичне відхилення (standart deviation) | \(s\), \(sd\) | \(\sigma\) |
| Дисперсія (variance) | \(s^2\), \(D\), \(Var\) | \(\sigma^2\), \(D\), \(Var\) |
| Стандартна похибка (standart error) | \(SE\), \(SEM\) | - |
| Коефіцієнт кореляції (correlation coef.) | \(r\) | \(p\) |
| Розмір вибірки (size) | \(n\) | \(N\) |
Систематична похибка відбору
Відноситься до практики упередженого підбору даних - свідомо чи несвідомо.
Таким чином, що вона призводить до оманливого або недовговічним висновку.
Нормальний розподіл
Нормальний розподіл
Унімодальний розподіл - розподіл, яке має тільки одну моду.
Нормальний розподіл - основний розподіл статистики. Його характерними рисами є унімодальність, симетричність, а також те, що відхилення спостережень від середнього підпорядковується ймовірнісному закону - законку нормального розподілу.
.svg.png)
Стандартний нормальний розподіл - це такий розподіл, в якому одиниці на осі x виражені в стандартних відхиленнях від середнього.
Нормальний розподіл
Формула нормального розподілу:
\[P(x) = \frac{e^{-(x - \mu)^{2}/(2\sigma^{2}) }} {\sigma\sqrt{2\pi}}\]

Нормальний розподіл
Z-стандартизація - перетворення нормального розподілу, що дозволяє змістити математичне очікування в 0, а дисперсію зробити рівний 1. Таке перетворення корисно, коли ми хочемо з’ясувати який відсоток спостережень лежить вище або нижче певного значення. В такому випадку можна користуватися стандартними таблицями Z-стандартизації.
\[z_i = \frac{x_i - \overline{x}}{\sigma_x}\]
\(z_i\) - стандартизоване значення.
\(x_i\) - спостереження.
\(\sigma_x\) - вибіркове середнє.
Правило:
У діапазоні \(M_x \pm \sigma\) знаходиться приблизно 68% спостережень
У діапазоні \(M_x \pm 2\sigma\) знаходиться приблизно 95% спостережень
У діапазоні \(M_x \pm 3\sigma\) знаходиться приблизно 100% спостережень
Нормальний розподіл
Q-Q plot (графік квантиль-квантиль) - показує наскільки вибіркове значення відповідає нормальному розподілу, лінія - ідеальне нормальне.
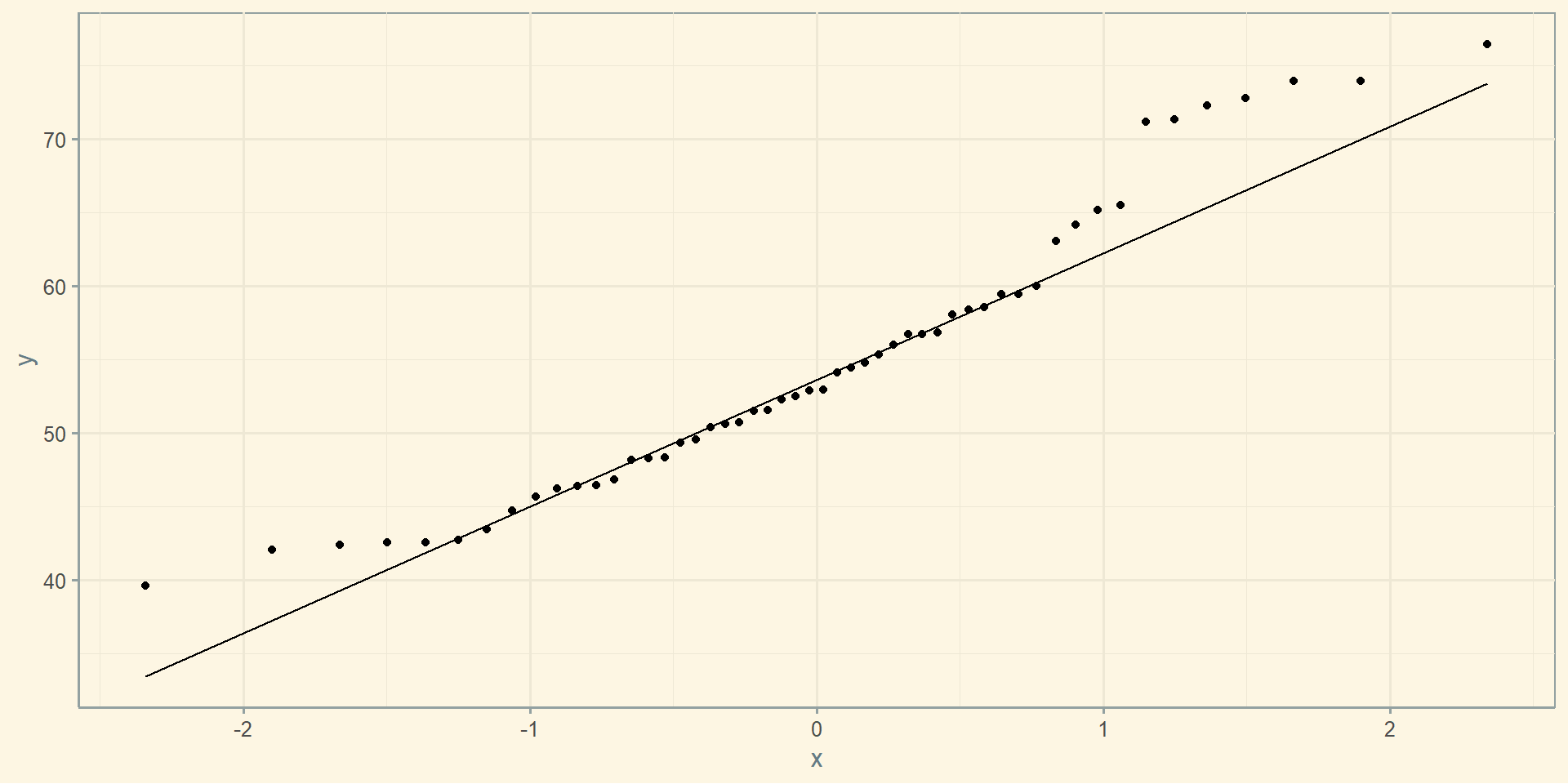
Розподіли в R
В R є свій набір з трьох основних функцій для кожного розподілу і ще одна функція: генератор випадкових чисел з обраного розподілу.
Ось ці функції:
d*()- функція ймовірності (probability mass function) для дискретних розподілів і функція щільності ймовірності для безперервних розподілів.p*()- функція накопиченої щільності розподілу (cumulative distribution function; cdf)q*()- квантільная функція (quantile function), або зворотна функція накопиченої щільності розподілу (inverse cumulative distribution function)r*()- для створення випадкових вибірок з обраного розподілу.
Розподіли в R
| Вибадкова вибірка | Функція щільності | Кумулятивна щільніть | Квантиль функція | |
|---|---|---|---|---|
| Нормальний розподіл | rnrom |
dnorm |
pnorm |
qnorm |
| Пуассонівський розподіл | rpois |
dpois |
ppois |
qpois |
| Біноміальний розподіл | rbinom |
dbinom |
pbinom |
qbinom |
| Рівномірний розподіл | runif |
dunif |
punif |
qunif |
Нормальний розподіл
Функція dnorm () має наступні основні параметри: x = - вектор прийнятих значень, середнє і стандартне відхилення ( mean = і sd =).
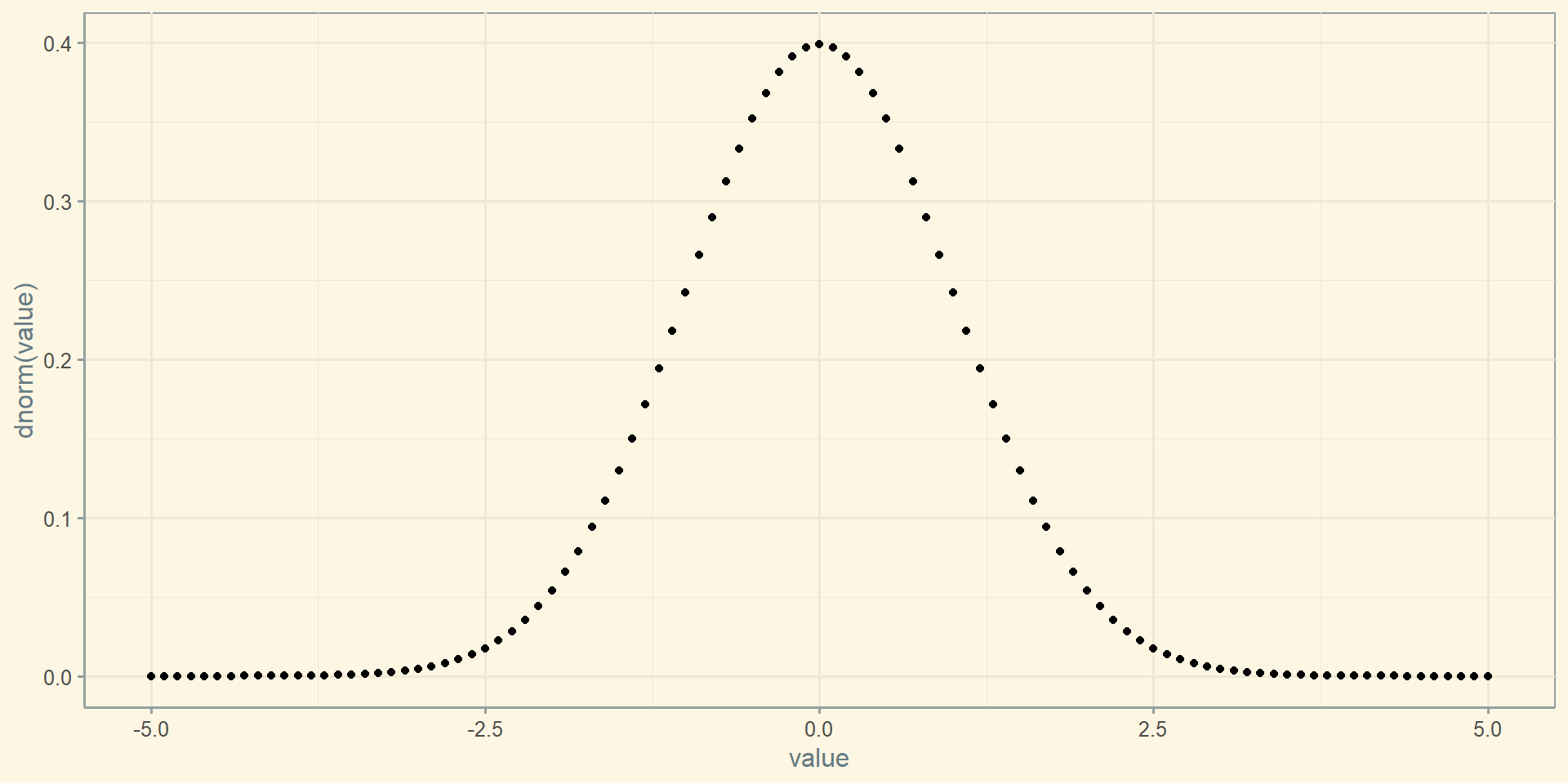
Нормальний розподіл
Середнє - 100, стандартне відхилення - 25.
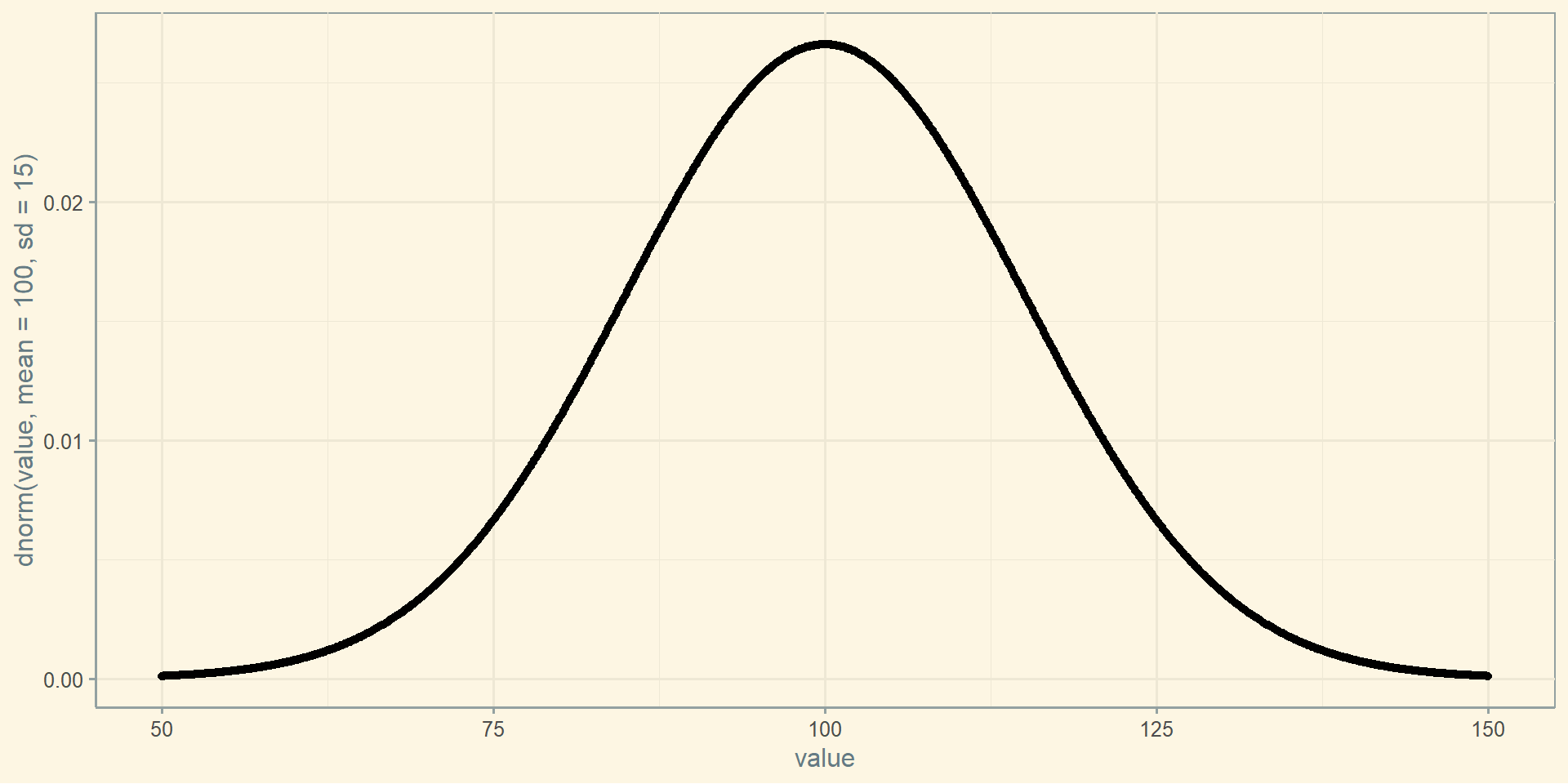
Функція кумулятивної щільності розподілу
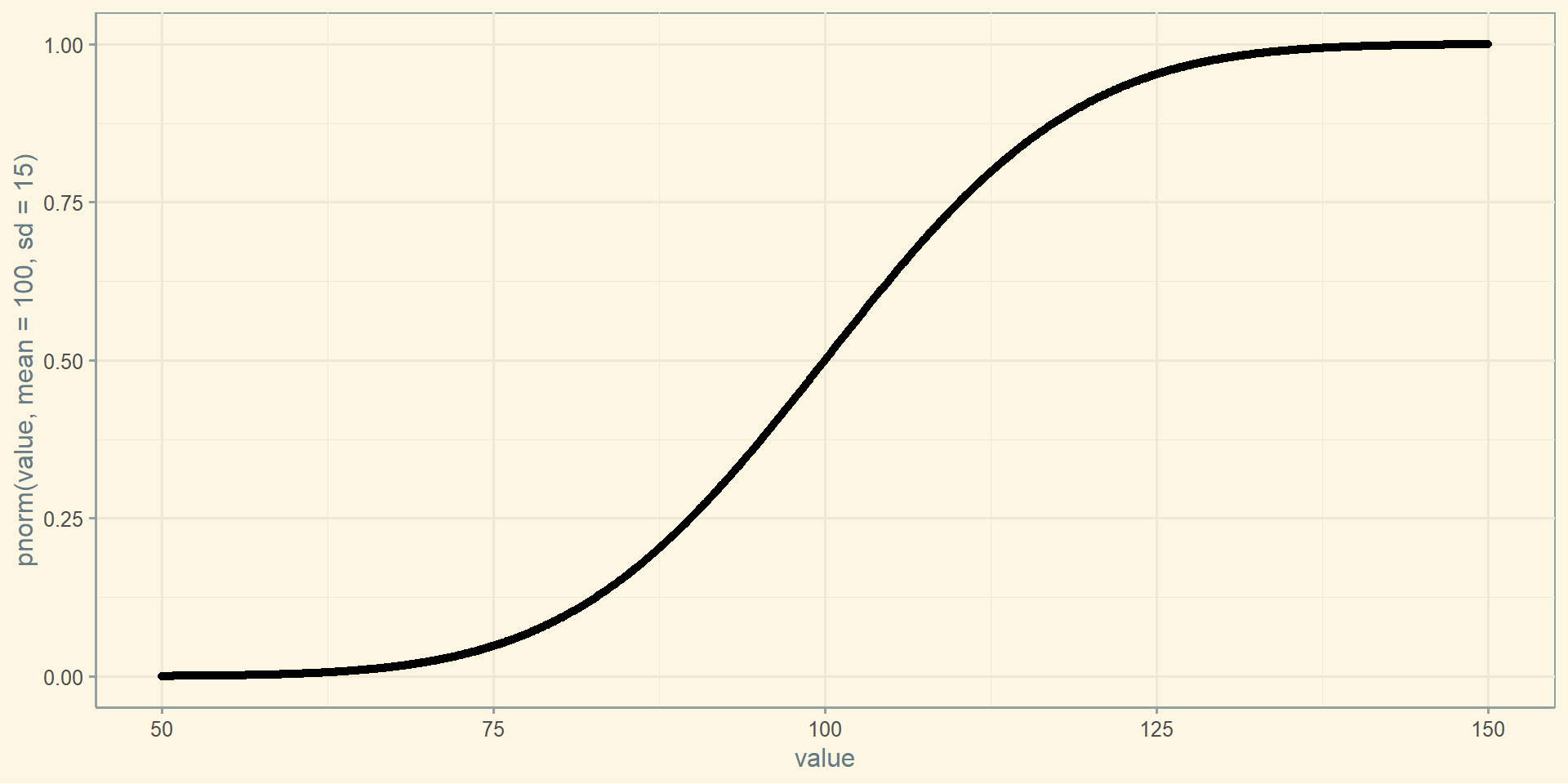
Функція кумулятивної щільності розподілу
Яка ймовірність того, що отримане випадкове значення IQ буде менше або дорівнює 100?
Менше або дорівнює 130:
Квантильна функція
Квантильна функція повертає значення, яке по заданій ймовірності випадкова змінна не буде перевищувати. Оскільки квантильна функція - це функція від імовірності, квантильна функція визначена на відрізку від 0 до 1.
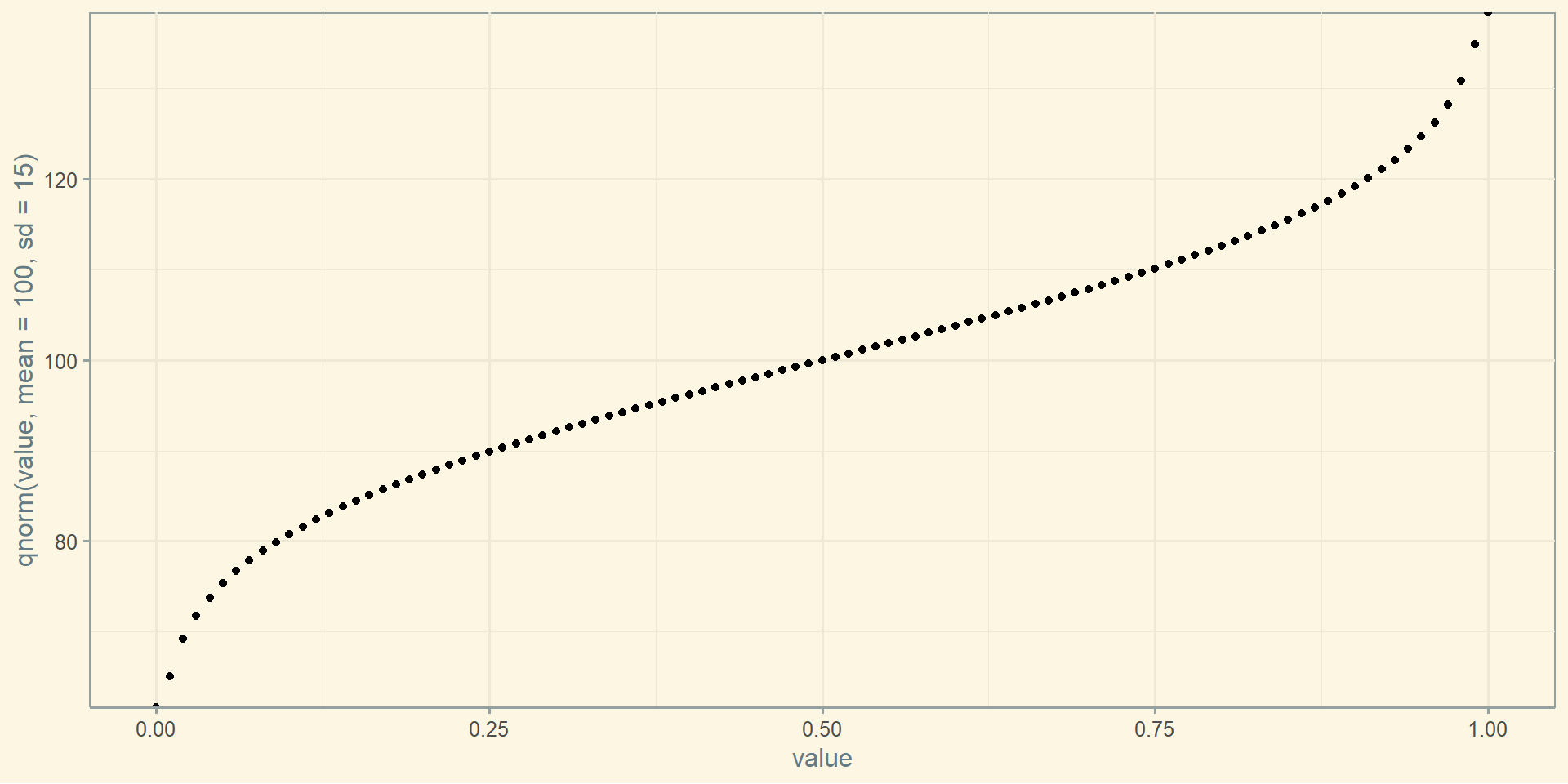
Випадкова вибірка
rnorm () - генерує вибірку значень з даного розподілу заданої довжини n =:
[1] 113.50213 82.39981 86.53772 78.33248 95.03480 56.49057
Центральна гранична теорема
Розподіл даних vs. розподіл вибірки
Розподіл вибіркової статистики, такої як середнє, ймовірно, буде більш регулярним і дзвоноподібним, ніж розподіл самих даних. Чим більше вибірка, на якій ґрунтується статистика, тим більш правдоподібною вона є.
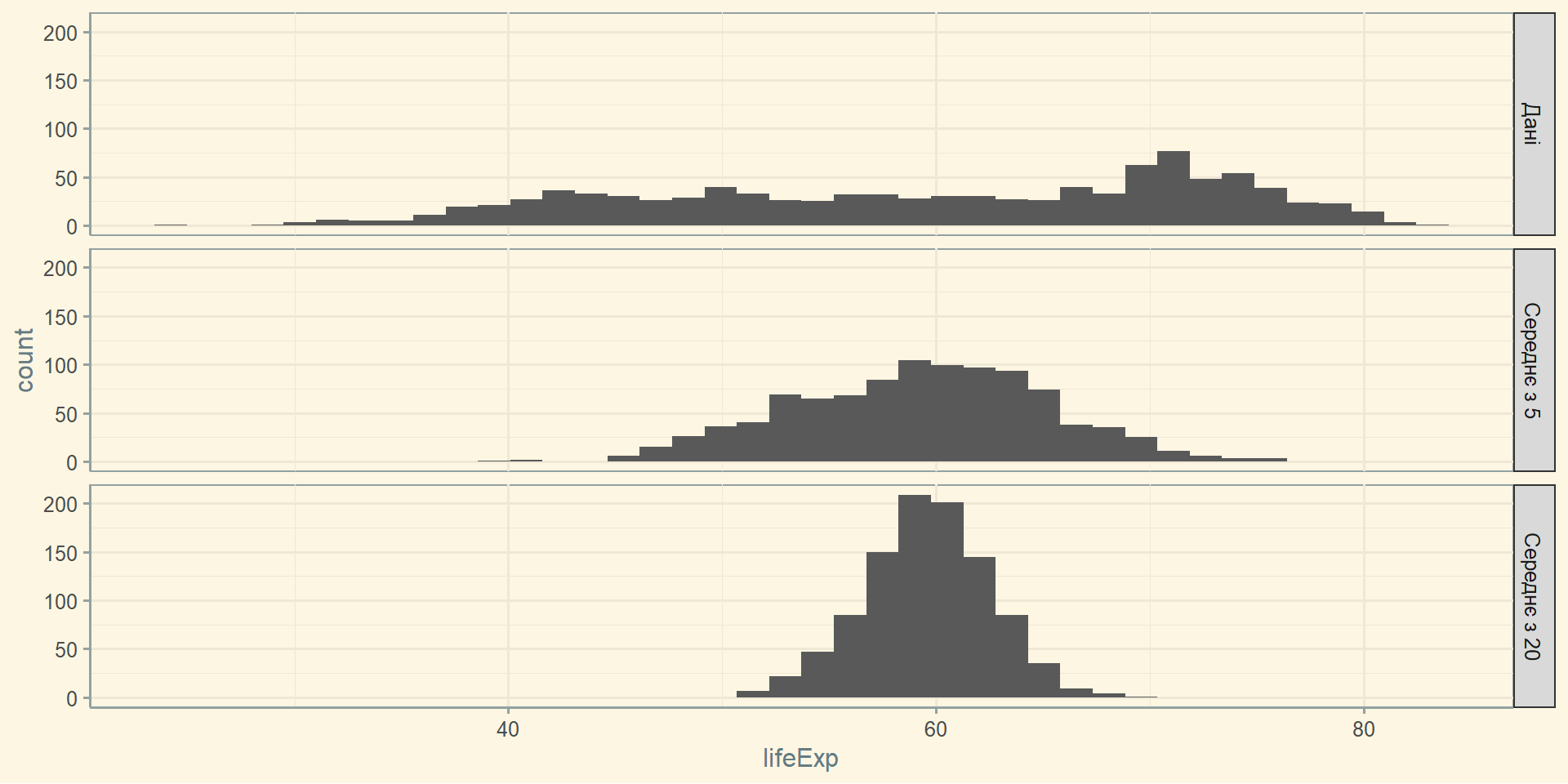
Обидві гістограми середніх з 5 і 20 значень більш компактні і більш дзвоноподібні.
Центральна гранична теорема (central limit theorem)
ЦГТ - припустимо у нас є деякий розподіл у ГС із середнім \(\mu\) і стандартним відхиленням \(\sigma\). Тоді розподіл вибіркових середніх (sampling distribution) буде прямувати до нормального із середнім рівним середньому в ГС і стандартним відхиленням рівним \(\frac{\sigma}{\sqrt{n}}\), де \(n\) - це розмір вибірки (за умови достатнього розміру вибірки).
Стандартна похибка середнього
\[SE_x = \frac{\sigma}{\sqrt{n}}\]
Алгоритм: 1. Отримати кілька абсолютно нових вибірок з ГС. 2. Для кожної нової вибірки обчислити статистику (наприклад, середнє). 3. Розрахувати стандартне відхилення статистики, обчисленої на кроці 2; використовувати її в якості оцінки стандартної помилки.
Стандартне відхилення vs. Стандартна похибка
Не плутайте стандартне відхилення (яке показує розсіювання окремих точок даних) зі стандартною помилкою (яка показує розсіювання вибіркового метричного показника).
Shiny App: Central Limit Theorem for Means
Бутсрап (bootstrap)
Виймаємо додаткові вибірки з поверненням із самої вибірки і повторно обчислювати статистику або модель для кожної повторної вибірки.

Бутсрап (bootstrap)
Алгоритм: 1. Вийняти вибіркове значення, записати його і повернути назад.
Повторити \(n\) разів.
Записати середнє для \(n\) повторно випробуваних значень.
Повторити кроки 1-3 \(R\) раз.
Використовувати \(R\) результатів, щоб:
- обчислити їх стандартне відхилення (воно оцінює стандартну помилку вибіркового середнього);
- побудувати гістограму або boxplot;
- знайти довірчий інтервал.
Бутсрап (bootstrap)
Бутстрап не компенсує малий розмір вибірки; він не створює нові дані і при цьому не заповнює дірки в існуючому наборі даних. Він просто повідомляє про те, як поведуть себе численні додаткові вибірки, коли вони будуть вийматися з популяції, такий як наша вихідна вибірка.
Довірчі інтервали
Довірчі інтервали
Довірчі інтервали - типовий спосіб представити оцінки у вигляді інтервального діапазону.
Довірчий інтервал середнього, 95%:
\[[\mu - 1.96\sigma, \mu + 1.96\sigma]\]
Довірчий інтервал середнього, 99%:
\[[\mu - 2.58\sigma, \mu + 2.58\sigma]\]
Довірчі інтервали
Проведено симуляцію довірчих інтервалів
Ми хочемо відловити симетрично 95% від площі під кривою. Для цього нам потрібно відкинути по 2.5% з обох сторін. Ці 2.5% становлять майже два стандартних відхилень від середнього. Якщо бути точніше, то 1.96. Якщо бути ще точніше:
Це кількість стандартних відхилень від середнього в нормальному розподілі, яке включає в себе рівно 95% площі нормального розподілу. Тепер давайте порахуємо стандартну помилку. Тут ми знаємо стандартне відхилення в генеральній сукупності (це 15), його поділимо на корінь з розміру вибірки:
Проведено симуляцію довірчих інтервалів
Щоб порахувати нижню і верхню границю довірчого інтервалу, нам потрібно відняти і додати відповідно потрібну кількість стандартних помилок:
Проведено симуляцію довірчих інтервалів
library(tidyverse)
sample_size <- 100
set.seed(2021)
ci_simulations <- tibble(
m = replicate(sample_size, mean(rnorm(sample_size, mean = 100, sd = 15))),
se = 15/sqrt(sample_size),
lower = m - se*zcr,
higher = m + se*zcr,
parameter_inside = lower<100 & higher>100
)
ci_simulations# A tibble: 100 x 5
m se lower higher parameter_inside
<dbl> <dbl> <dbl> <dbl> <lgl>
1 97.4 1.5 94.4 100. TRUE
2 100. 1.5 97.0 103. TRUE
3 100. 1.5 97.1 103. TRUE
4 98.4 1.5 95.5 101. TRUE
5 104. 1.5 102. 107. FALSE
6 97.7 1.5 94.8 101. TRUE
7 101. 1.5 98.4 104. TRUE
8 103. 1.5 100. 106. FALSE
9 100. 1.5 97.2 103. TRUE
10 99.3 1.5 96.4 102. TRUE
# ... with 90 more rowsПроведено симуляцію довірчих інтервалів
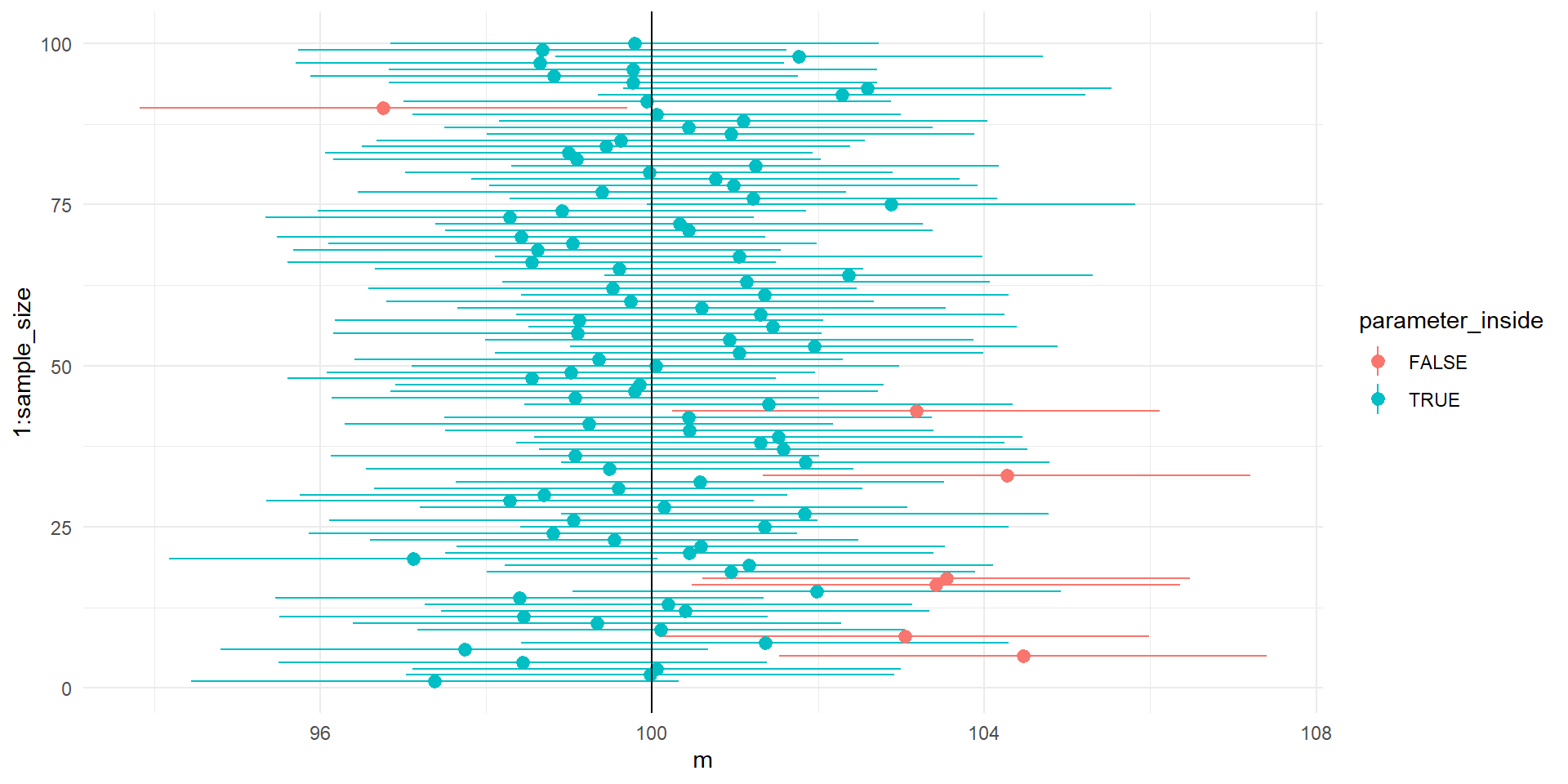
Дякую за увагу!
ihor.miroshnychenko@kneu.ua
