| p | odds | log_odds |
|---|---|---|
| 0.01 | 0.01 | -4.60 |
| 0.02 | 0.02 | -3.89 |
| 0.03 | 0.03 | -3.48 |
| 0.04 | 0.04 | -3.18 |
| 0.05 | 0.05 | -2.94 |
| 0.06 | 0.06 | -2.75 |
| 0.07 | 0.08 | -2.59 |
| 0.08 | 0.09 | -2.44 |
| 0.09 | 0.10 | -2.31 |
| 0.10 | 0.11 | -2.20 |
| 0.11 | 0.12 | -2.09 |
| 0.12 | 0.14 | -1.99 |
| 0.13 | 0.15 | -1.90 |
| 0.14 | 0.16 | -1.82 |
| 0.15 | 0.18 | -1.73 |
| 0.16 | 0.19 | -1.66 |
| 0.17 | 0.20 | -1.59 |
| 0.18 | 0.22 | -1.52 |
| 0.19 | 0.23 | -1.45 |
| 0.20 | 0.25 | -1.39 |
| 0.21 | 0.27 | -1.32 |
| 0.22 | 0.28 | -1.27 |
| 0.23 | 0.30 | -1.21 |
| 0.24 | 0.32 | -1.15 |
| 0.25 | 0.33 | -1.10 |
| 0.26 | 0.35 | -1.05 |
| 0.27 | 0.37 | -0.99 |
| 0.28 | 0.39 | -0.94 |
| 0.29 | 0.41 | -0.90 |
| 0.30 | 0.43 | -0.85 |
| 0.31 | 0.45 | -0.80 |
| 0.32 | 0.47 | -0.75 |
| 0.33 | 0.49 | -0.71 |
| 0.34 | 0.52 | -0.66 |
| 0.35 | 0.54 | -0.62 |
| 0.36 | 0.56 | -0.58 |
| 0.37 | 0.59 | -0.53 |
| 0.38 | 0.61 | -0.49 |
| 0.39 | 0.64 | -0.45 |
| 0.40 | 0.67 | -0.41 |
| 0.41 | 0.69 | -0.36 |
| 0.42 | 0.72 | -0.32 |
| 0.43 | 0.75 | -0.28 |
| 0.44 | 0.79 | -0.24 |
| 0.45 | 0.82 | -0.20 |
| 0.46 | 0.85 | -0.16 |
| 0.47 | 0.89 | -0.12 |
| 0.48 | 0.92 | -0.08 |
| 0.49 | 0.96 | -0.04 |
| 0.50 | 1.00 | 0.00 |
| 0.51 | 1.04 | 0.04 |
| 0.52 | 1.08 | 0.08 |
| 0.53 | 1.13 | 0.12 |
| 0.54 | 1.17 | 0.16 |
| 0.55 | 1.22 | 0.20 |
| 0.56 | 1.27 | 0.24 |
| 0.57 | 1.33 | 0.28 |
| 0.58 | 1.38 | 0.32 |
| 0.59 | 1.44 | 0.36 |
| 0.60 | 1.50 | 0.41 |
| 0.61 | 1.56 | 0.45 |
| 0.62 | 1.63 | 0.49 |
| 0.63 | 1.70 | 0.53 |
| 0.64 | 1.78 | 0.58 |
| 0.65 | 1.86 | 0.62 |
| 0.66 | 1.94 | 0.66 |
| 0.67 | 2.03 | 0.71 |
| 0.68 | 2.13 | 0.75 |
| 0.69 | 2.23 | 0.80 |
| 0.70 | 2.33 | 0.85 |
| 0.71 | 2.45 | 0.90 |
| 0.72 | 2.57 | 0.94 |
| 0.73 | 2.70 | 0.99 |
| 0.74 | 2.85 | 1.05 |
| 0.75 | 3.00 | 1.10 |
| 0.76 | 3.17 | 1.15 |
| 0.77 | 3.35 | 1.21 |
| 0.78 | 3.55 | 1.27 |
| 0.79 | 3.76 | 1.32 |
| 0.80 | 4.00 | 1.39 |
| 0.81 | 4.26 | 1.45 |
| 0.82 | 4.56 | 1.52 |
| 0.83 | 4.88 | 1.59 |
| 0.84 | 5.25 | 1.66 |
| 0.85 | 5.67 | 1.73 |
| 0.86 | 6.14 | 1.82 |
| 0.87 | 6.69 | 1.90 |
| 0.88 | 7.33 | 1.99 |
| 0.89 | 8.09 | 2.09 |
| 0.90 | 9.00 | 2.20 |
| 0.91 | 10.11 | 2.31 |
| 0.92 | 11.50 | 2.44 |
| 0.93 | 13.29 | 2.59 |
| 0.94 | 15.67 | 2.75 |
| 0.95 | 19.00 | 2.94 |
| 0.96 | 24.00 | 3.18 |
| 0.97 | 32.33 | 3.48 |
| 0.98 | 49.00 | 3.89 |
| 0.99 | 99.00 | 4.60 |
Логістична регресія
Кількісні методи в економіці
КНЕУ імені Вадима Гетьмана, ІІТЕ
Основні поняття
Логістична регресія
Залежна змінна - номінативна змінна з двома рівнями: 0 та 1
Незалежні змінні - кількісні та якісні.
Основна суть: розглянути задачу класифікації, як на задачу передбачення ймовірностей.
Ймовірність та шанси
Проблема: ймовірність має бути у діапазоні від 0 до 1, а простого способу навчити лінійну модель відповідала таким умовам - не має.
Вихід: навчити лінійну модель правильно передбачати якийсь об’єкт пов’язаний з ймовірністю, але в діапазоні \((-\infty, +\infty)\) та перетворити відповіді у ймовірності.
Таким об’єктом є logit або log odds - логарифм відношень шансів позитивної події до негативної \(log(\frac{p}{1-p})\)
Приклад: маємо випадкову величину з двома рівнями, тоді шанси (odds) - це відношення ймовірності позитивних подій до негативних.
Орел (+) випав 2 рази, Решка (-): 8.
Ймовірність орла: \(p = \frac{2}{2+8} = 0.2\)
Шанс орла: \(odds = \frac{p}{1-p} = \frac{0.2}{1-0.2} = \frac{2}{8} = 0.25\)
Ймовірності -> Шанси -> Логарифм шансів
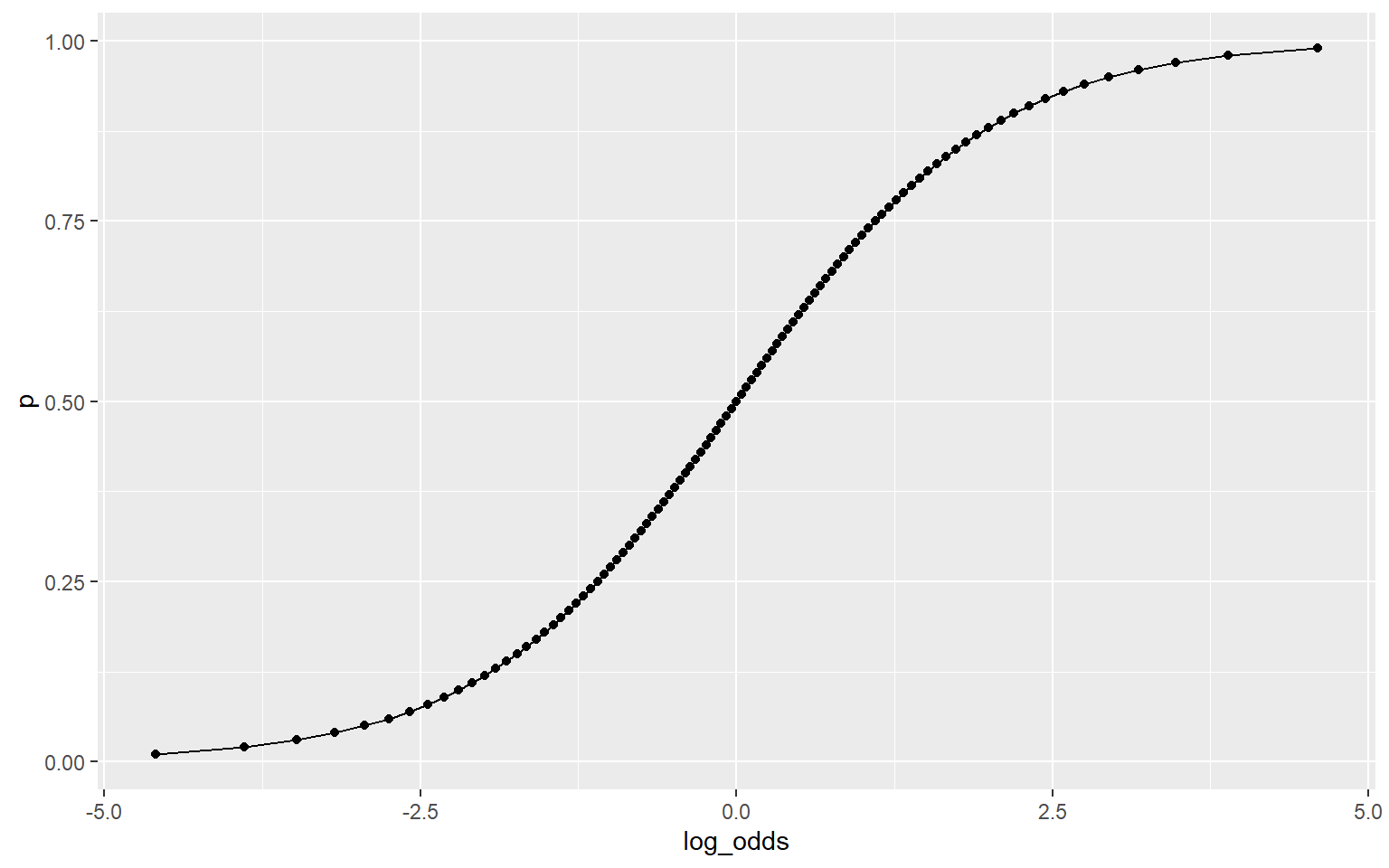
\(logit(p) = log(\frac{p}{1-p}) = \beta_0 + \beta_1*x_1\) \(p = \frac{exp(\beta_0 + \beta_1*x_1)}{(1 + exp(\beta_0 + \beta_1*x_1)}\)
Модель без предикторів
Модель без предикторів
Модель без предикторів
Модель без предикторів
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | -0.4732877 | 0.0688874 | -6.870457 | 0 |
- \(H_0\): шанс = 1 (або шанс вижити 1:1, або ймовірність вижити 0.5)
- За умови \(H_0\) ми отримуємо нормальний розподіл, оскільки не має різниці між виходами.
- Тоді стандартне похибка \(se = \sqrt{\frac{1}{n_0}+\frac{1}{n_1}} = 0.06888737\)
- \(z_{value}\) - кількість стандартних відхилень
- \(z_{value} = \frac{log(odds)}{sd} = \frac{b_0}{se} = -6.870457\)
- \(p_{value} = 2 * \Phi(\frac{-|\beta|}{SE(\beta)})\), де \(\Phi\) - кумулятивна функція нормального стандартного розподілу
Модель з одним номінативним предиктором
Модель з одним номінативним предиктором
Модель з одним номінативним предиктором
Survived ~ Sex
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 1.056589 | 0.1289864 | 8.191477 | 0 |
| SexMale | -2.513710 | 0.1671782 | -15.036107 | 0 |
| Female | Male | |
|---|---|---|
| No | 81 | 468 |
| Yes | 233 | 109 |
Інтерпретація:
Дивимось на градації факторів для інтерпретації
InterceptIntercept- натуральний логарифм шансів позитивного результату для жінокКоефіцієнт біля
SexMale- логарифм відношення шансів позитивного результату для чоловіків і шансів для жінок.
Модель з одним номінативним предиктором
Рівняння регресії: \[ln(odds) = Intercept + \beta_1 * SexMale\]
Значення
Intercept- це логарифм шансів вижити для жінок: \[Intercept = ln(\frac{p_{surv}}{1-p_{surv}}) = ln(odds_{female})\]Значення коефіцієнта при
SexMale- це логарифм відношення шансів вижити для чоловіків і шансів вижити для жінок, але за властивістю логарифмів ми можемо уявити логарифм відношення як різниця логарифмів: \[\beta_1 = ln(\frac{odds_{male}}{odds_{female}})=ln(odds_{male}) - ln(odds_{female})\]
Таким чином, коефіцієнт при SexMale – це різниця логарифмів шансів. Іншими словами, це ціна переходу з однієї градації нашої ознаки на іншу!
Модель з одним номінативним предиктором
- Розглянемо завдання передбачення. Якщо новий пасажир - жінка, тоді значення змінної
SexMale= 0 і ми отримаємо логарифм шансів для жінок:
\[ln(odds_{female}) = ln(odds_{female}) + 0 * (ln(odds_{male})-ln(odds_{female}))\]
- Тепер, зробимо прогноз для пасажира чоловіка, у цьому випадку SexMale = 1, шанси для жінок скоротяться, і ми отримаємо шанси для чоловіків: \[ln(odds_{male}) = ln(odds_{female}) + 1 * (ln(odds_{male})-ln(odds_{female}))= \\ ln(odds_{female}) + ln(odds_{male})-ln(odds_{female})\]
Модель з двома номінативними предикторами
Модель з двома номінативними предикторами
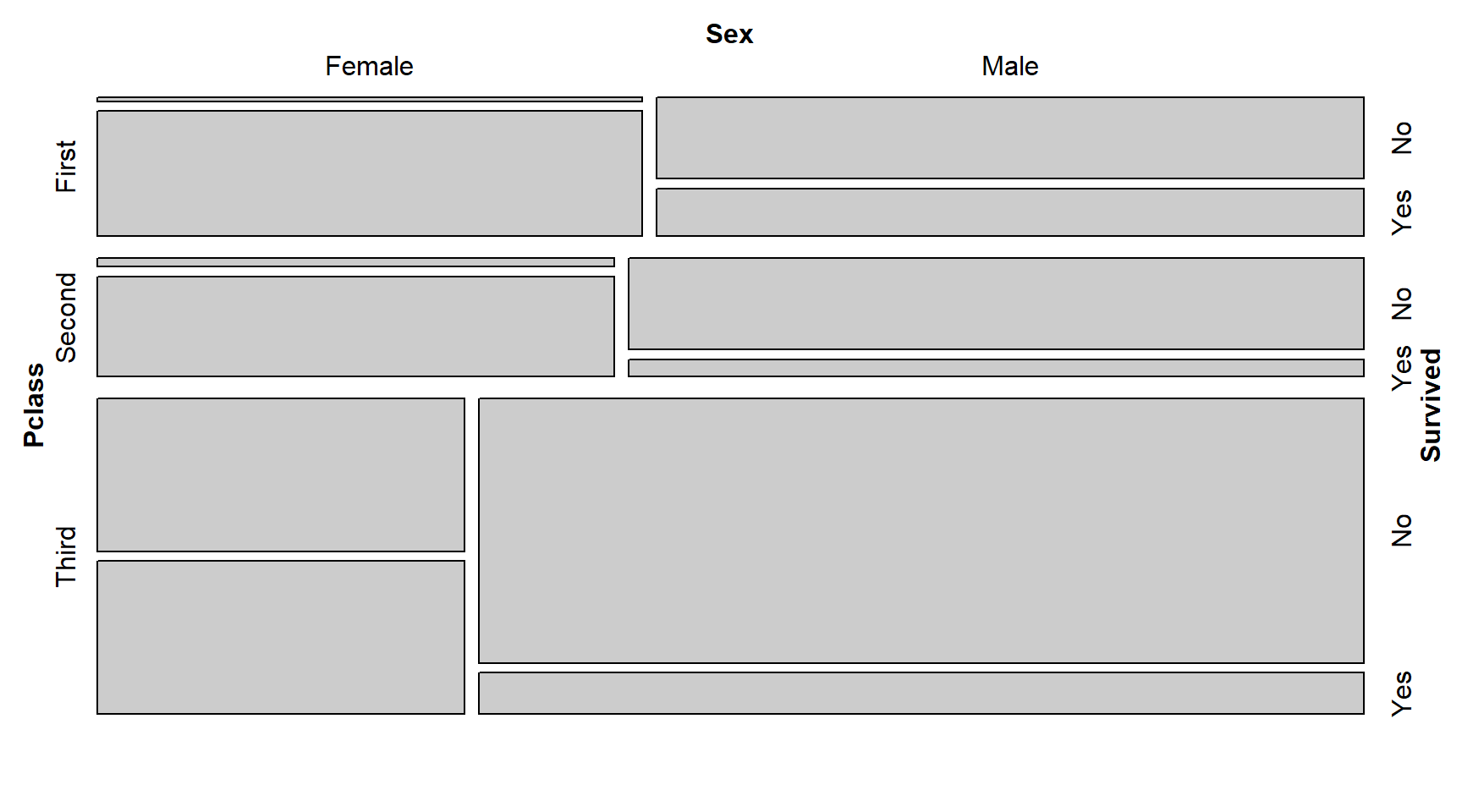
Модель з двома номінативними предикторами
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.4122472 0.5867893 5.815115 6.059214e-09
SexMale -3.9493901 0.6160608 -6.410715 1.448386e-10
PclassSecond -0.9555114 0.7247579 -1.318387 1.873741e-01
PclassThird -3.4122472 0.6099995 -5.593852 2.220860e-08
SexMale:PclassSecond -0.1849918 0.7939117 -0.233013 8.157513e-01
SexMale:PclassThird 2.0957553 0.6572051 3.188891 1.428199e-03Модель з двома номінативними предикторами
Модель з двома номінативними предикторами
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 3.4122472 | 0.5867893 | 5.815115 | 0.0000000 |
| SexMale | -3.9493901 | 0.6160608 | -6.410715 | 0.0000000 |
| PclassSecond | -0.9555114 | 0.7247579 | -1.318387 | 0.1873741 |
| PclassThird | -3.4122472 | 0.6099995 | -5.593852 | 0.0000000 |
| SexMale:PclassSecond | -0.1849918 | 0.7939117 | -0.233013 | 0.8157513 |
| SexMale:PclassThird | 2.0957553 | 0.6572051 | 3.188891 | 0.0014282 |
\(ln(\frac{odds_{male}}{odds_{female}}) = ln(odds_{male}) - ln(odds_{female})\)
SexMale - логарифм відношення шансів для чоловіків і жінок у першому класі.
Модель з двома номінативними предикторами
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 3.4122472 | 0.5867893 | 5.815115 | 0.0000000 |
| SexMale | -3.9493901 | 0.6160608 | -6.410715 | 0.0000000 |
| PclassSecond | -0.9555114 | 0.7247579 | -1.318387 | 0.1873741 |
| PclassThird | -3.4122472 | 0.6099995 | -5.593852 | 0.0000000 |
| SexMale:PclassSecond | -0.1849918 | 0.7939117 | -0.233013 | 0.8157513 |
| SexMale:PclassThird | 2.0957553 | 0.6572051 | 3.188891 | 0.0014282 |
\(ln(\frac{odds_{f_2}}{odds_{f_1}}) = ln(odds_{f_2}) - ln(odds_{f_1})\)
PclassSecond - логарифм відношення шансів для жінок у другому класі і жінок у першому класі.
Модель з двома номінативними предикторами
Модель зі взаємодією номінативних предикторів
Модель зі взаємодією номінативних предикторів
Модель зі взаємодією номінативних предикторів
SexMale:PclassSecond - різниція логарифмів відношення шансів для чоловіків і жінок другого та першого класу.
\[ln(\frac{odds_{male-2}}{odds_{female-2}}) - ln(\frac{odds_{male-1}}{odds_{female-1}}) = ln(\frac{odds_{male-2} * odds_{female-1}}{odds_{female-2} * odds_{male-1}})\]
Взаємодія двох факторів говорить нам про те, що взаємодія між статтю пасажира і його статусом виявляється різною в залежності від від класу кают пасажирів.
Модель зі взаємодією номінативних предикторів
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 3.4122472 | 0.5867893 | 5.815115 | 0.0000000 |
| SexMale | -3.9493901 | 0.6160608 | -6.410715 | 0.0000000 |
| PclassSecond | -0.9555114 | 0.7247579 | -1.318387 | 0.1873741 |
| PclassThird | -3.4122472 | 0.6099995 | -5.593852 | 0.0000000 |
| SexMale:PclassSecond | -0.1849918 | 0.7939117 | -0.233013 | 0.8157513 |
| SexMale:PclassThird | 2.0957553 | 0.6572051 | 3.188891 | 0.0014282 |
Intercept - натуральний логарифм шансів позитивного виходу для жінок
SexMale - логарифм відношення шансів позитивного виходу для чоловіків і шансів для жінок.
PclassSecond - логарифм відношення шансів для жінок у другому класі і жінок у першому класі.
PclassThird - логарифм відношення шансів для жінок у третьому класі і жінок у першому класі.
SexMale:PclassSecond - різниція логарифмів відношення шансів для чоловіків і жінок другого та першого класу.
SexMale:PclassThird - різниція логарифмів відношення шансів для чоловіків і жінок третього та першого класу.
Модель зі взаємодією номінативних предикторів
Формула для розрахунку ймовірності: \[p = \frac{x}{1+x}\] де, \(x\) - значення шансів.
Модель зі взаємодією номінативних предикторів
Call:
glm(formula = Survived ~ Sex + Pclass + Age, family = "binomial",
data = titanic)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.777013 0.401123 9.416 < 2e-16 ***
SexMale -2.522781 0.207391 -12.164 < 2e-16 ***
PclassSecond -1.309799 0.278066 -4.710 2.47e-06 ***
PclassThird -2.580625 0.281442 -9.169 < 2e-16 ***
Age -0.036985 0.007656 -4.831 1.36e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 647.28 on 709 degrees of freedom
(177 observations deleted due to missingness)
AIC: 657.28
Number of Fisher Scoring iterations: 5Дякую за увагу!
