07 - Ансамблі 🌲🌲🌲🎄🌲

Machine Learning

Ігор Мірошниченко

КНЕУ::ІІТЕ

2023-05-16

Ансамблеві методи

Основи

Замість того, щоб зосереджуватися на навчанні високоточної однієї моделі, ансамблеві методи поєднують багато моделей низької точності в мета-модель.

Три поширені методи для комбінування окремих дерев

  1. Bagging
  2. Random forests
  3. Boosting

Чому? Хоча окремі дерева можуть бути дуже різними та неточними, Комбінація дерев часто досить стабільна і точна.

Bagging

Bagging

Bagging створює додаткові зразки через бутсрап.

Q Як допомагає бутсрап?

A Окремі дерева рішень страждають від варіативності (non-robust).

Ця неробастість означає, що дерева можуть сильно змінюватись в залежності ві того, які спостереження включені/виключені.

По суті, ми використовуємо багато «симуляцій» замість одного набору даних1

Bagging

Bootstrap aggregation (bagging) зменшує цей тип мінливості.

  1. Створіть \(B\) зразків початкові вибірки з поверненням.
  2. Навчіть оцінювач (дерево) \(\color{#6A5ACD}{\mathop{\hat{f^b}}(x)}\) на кожній із вибірок \(B\)
  3. Об’єднайте ваші бустрап моделі \(B\):

\[ \begin{align} \color{#e64173}{\mathop{\hat{f}_{\text{bag}}}(x)} = \dfrac{1}{B}\sum_{b=1}^{B}\color{#6A5ACD}{\mathop{\hat{f^b}}(x)} \end{align} \]

Ця сукупна модель \(\color{#e64173}{\mathop{\hat{f}_{\text{bag}}}(x)}\) є вашою остаточною моделлю.

Bagging

Коли ми застосовуємо баггінг до дерев рішень,

  • ми зазвичай нарощуємо глибину дерева і не обрізаємо

  • для регресії ми усереднюємо по регіонах дерев \(B\)

  • для класифікація ми маємо більше варіантів, але часто беремо більшість

Окремі (необрізані) дерева будуть дуже гнучкими і зашумленими,
але їх узагальнення буде досить стабільним.

Кількість дерев \(B\), як правило, не є критичною для бєггінгу
\(B=100\) в більшості випадків є достатнім.

Out-of-bag error estimation

Бєггінг також пропонує зручний метод оцінки ефективності.

Для будь-якої початкової вибірки ми пропускаємо ~n/3 спостережень.

Out-of-bag (OOB) error estimation оцінює частоту помилок тесту, використовуючи спостереження випадково пропущених з кожного початкового зразка.

Для кожного спостереження \(i\):

  1. Знайти всі зразки \(S_i\), в яких \(i\) було пропущено у навчальній вибірці
  2. Узагальнюєте прогнози \(|S_i|\) \(\color{#6A5ACD}{\mathop{\hat{f^b}}(x_i)}\), наприклад, використовуючи їхнє середнє або моду
  3. Обчисліть похибку, наприклад, \(y_i - \mathop{\hat{f}_{i,\text{OOB},i}}(x_i)\)

Out-of-bag error estimation

Коли \(B\) достатньо великий, частота помилок OOB буде дуже близькою до LOOCV (Leave-One-Out Cross-Validation).

Q Навіщо використовувати коефіцієнт помилок OOB?

A Коли \(B\) і \(n\) великі, перехресна перевірка — з будь-якою кількістю згорток — може стати досить затратною для обчислень.





Ось інструмент для пошуку моделей parsnip:

https://www.tidymodels.org/find/parsnip/

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
  • tree_depth: макс. глибина дерева
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
  • tree_depth: макс. глибина дерева
  • min_n: мін. к-ть спостереж. для поділу
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
  • tree_depth: макс. глибина дерева
  • min_n: мін. к-ть спостереж. для поділу
  • class_cost: збільшення вартості мінорного класу
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
  • tree_depth: макс. глибина дерева
  • min_n: мін. к-ть спостереж. для поділу
  • class_cost: збільшення вартості мінорного класу
  • rpart є движком за замовчуванням
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
) %>% set_engine(
  engine = "rpart",
  times = 100
)

Bagging в R

Ми можемо використовувати tidymodels плюс пакет baguette для бєггінгу дерев.

Функція: bag_tree()

  • “Визначає” модель для parsnip.
  • mode: ‘class.’, ‘reg.’, або unknown
  • cost_complexity: штраф за складність моделі (Cp)
  • tree_depth: макс. глибина дерева
  • min_n: мін. к-ть спостереж. для поділу
  • class_cost: збільшення вартості мінорного класу
  • rpart є движком за замовчуванням
  • times: кількість дерев
# Train a bagged tree model
bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
) %>% set_engine(
  engine = "rpart",
  times = 100
)

Приклад: Bagging в R


OOB-based error

# Set the seed
set.seed(12345)
# Train the bagged trees
heart_bag = train(
  heart_disease ~ .,
  data = heart_df,
  method = "treebag",
  nbagg = 100,
  keepX = T,
  trControl = trainControl(
    method = "oob"
  )
)


CV-based error

# Set the seed
set.seed(12345)
# Train the bagged trees
heart_bag_cv = train(
  heart_disease ~ .,
  data = heart_df,
  method = "treebag",
  nbagg = 100,
  keepX = T,
  trControl = trainControl(
    method = "cv",
    number = 5
  )
)
# Set the seed
set.seed(12345)

plan(multisession)
# Train the bagged trees
bag_oob = future_map_dfr(
  .x = 2:300,
  .f = function(n) {
    train(
      heart_disease ~ .,
      data = heart_df,
      method = "treebag",
      nbagg = n,
      keepX = T,
      trControl = trainControl(
        method = "oob"
      )
    )$results$Accuracy %>%
    data.frame(accuracy = ., n_trees = n)
  }
)
# Train the bagged trees
bag_cv <- future_map_dfr(
  .x = 2:300,
  .f = function(n) {
    train(
      heart_disease ~ .,
      data = heart_df,
      method = "treebag",
      nbagg = n,
      keepX = T,
      trControl = trainControl(
        method = "cv",
        number = 5
      )
    )$results$Accuracy %>%
    data.frame(accuracy = ., n_trees = n)
  }
)

Bagging та кількість дерев






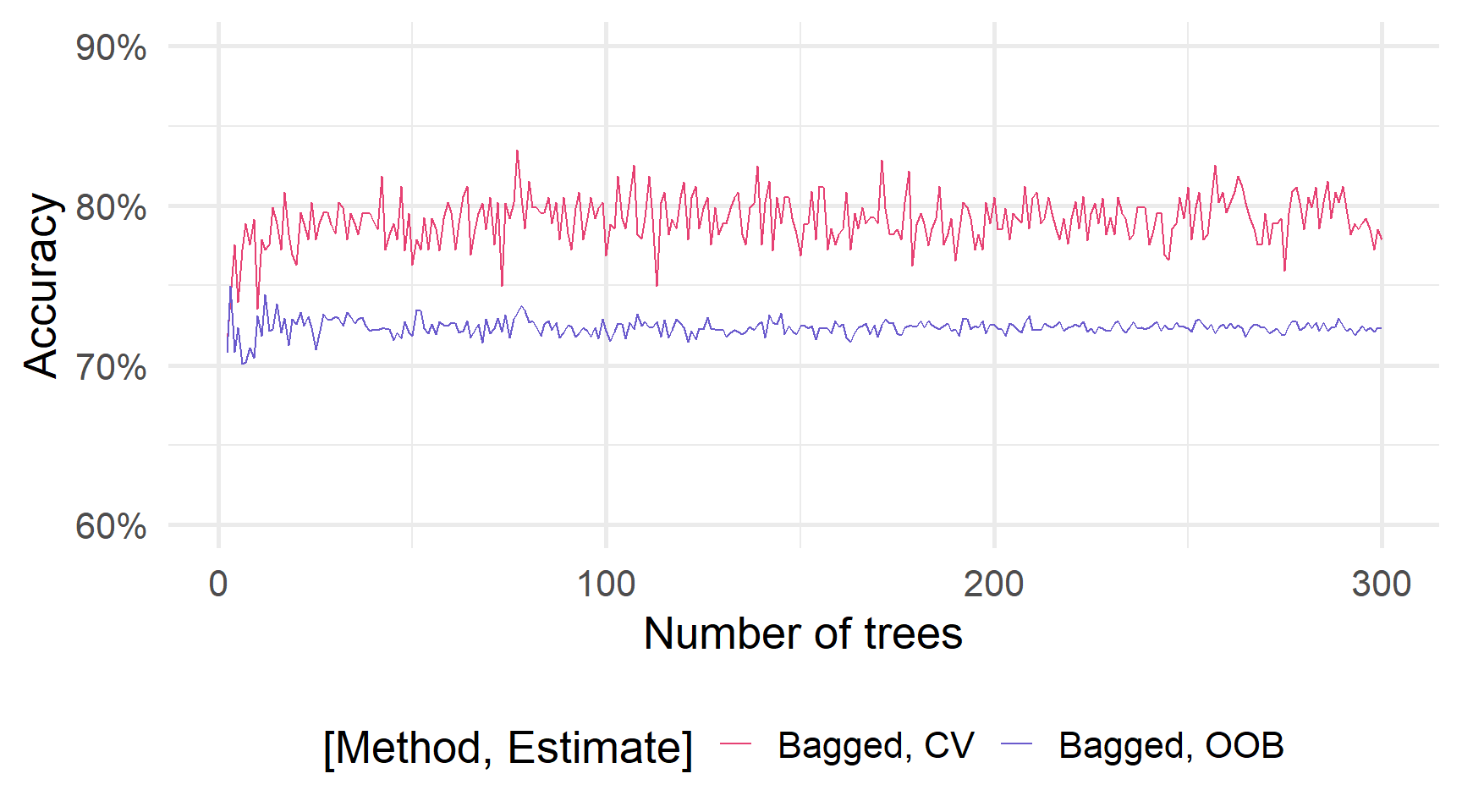
На жаль, ця комбінація rpart/baguette/parsnip/yardstick не пропонує (наразі) показники на основі OOB . 😞






Ми можемо “обдурити” випадкові ліси (ranger) у виконанні OOB для Bagging дерев.

Але спочатку нам потрібно дізнатися про випадкові ліси…





… і перед цим, давайте коротко поговоримо про впливовість змінних.

Впливовість змінних

Впливовість змінних

У той час як ансамблеві методи, як правило, покращують ефективність прогнозування, вони також мають тенденцію знижувати інтерпретованість.

Ми можемо проілюструвати важливість змінних, враховуючи зменшення показників ефективності моделі (RSS, Gini, ентропія тощо)1

У випадку "rpart" bagged дерев…

# Recipe to clean data (impute NAs)
heart_recipe = recipe(heart_disease ~ ., data = heart_df) %>% 
  step_impute_median(all_predictors() & all_numeric()) %>% 
  step_impute_mode(all_predictors() & all_nominal())
# Define the bagged tree model
heart_bag = bag_tree(
  mode = "classification",
  cost_complexity = 0,
  tree_depth = NULL,
  min_n = 2,
  class_cost = NULL
) %>% set_engine(
  engine = "rpart",
  times = 100
)
# Define workflow
heart_bag_wf = workflow() %>% 
  add_model(heart_bag) %>% 
  add_recipe(heart_recipe)
# Fit/assess with CV
heart_bag_fit = heart_bag_wf %>% fit(heart_df)

… оцінений об’єкт автоматично включає змінну важливість.

Bagged CART (classification with 100 members)

Variable importance scores include:

# A tibble: 13 × 4
   term       value std.error  used
   <chr>      <dbl>     <dbl> <int>
 1 max_hr     41.1      0.839   100
 2 chest_pain 36.9      1.18    100
 3 oldpeak    36.8      0.806   100
 4 thal       35.7      1.35    100
 5 age        32.2      0.702   100
 6 ca         26.8      1.18    100
 7 chol       23.2      0.685   100
 8 rest_bp    22.1      0.589   100
 9 ex_ang     20.6      0.818    99
10 slope      16.3      0.772   100
11 sex        11.8      0.678   100
12 rest_ecg    4.92     0.311    95
13 fbs         3.02     0.210    93

Важливість змінних з нашої bagged tree model.

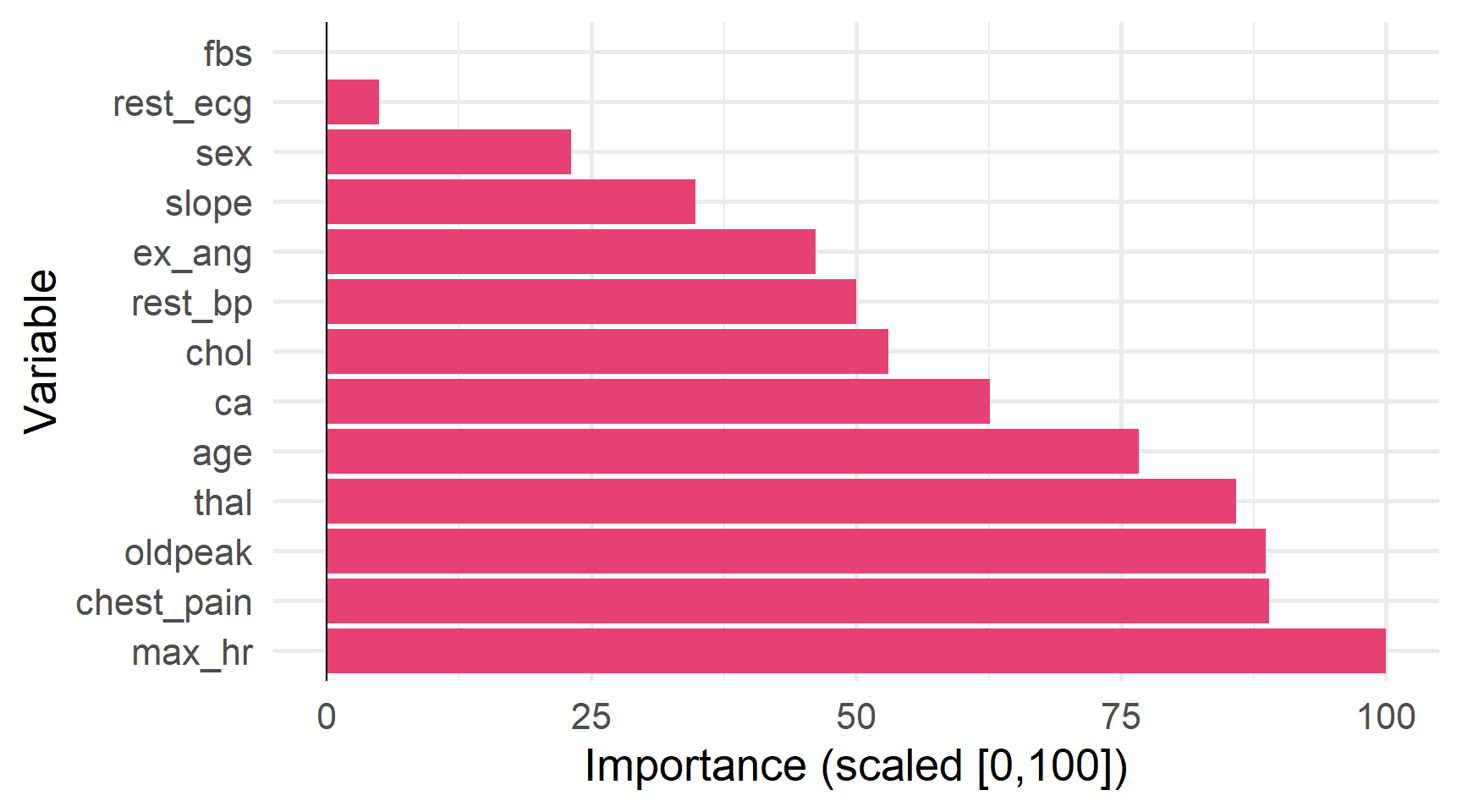
Bagging

У Bagging є ще один недолік…

Якщо одна змінна домінує над іншими змінними, дерева будуть дуже корельованими.

Якщо дерева дуже корельовані, то bagging втрачає свою перевагу.

Рішення Ми повинні зробити дерева менш корельованими.

Random forests

Random forests

Випадкові ліси покращують bagged trees шляхом декореляції дерев.

Щоб декорелювати дерева, випадковий ліс розглядає лише випадкову підмножину \(\color{#e64173}{m\enspace (\approx\sqrt{p})}\) предикторів при виконанні кожного розбиття (для кожного дерева).

Обмеження змінних, які наше дерево бачить при заданому розділенні:

  • не дозволяє деревам постійно використовувати одні і ті ж змінні,
  • збільшує різноманітність дерев у нашому лісі,
  • потенційно зменшує дисперсію наших оцінок.

Якщо наші прогнози дуже корельовані, ми можемо захотіти зменшити \(m\).

Random forests

Таким чином, випадкові ліси вводять два виміри випадкової варіації

  1. бутсрап вибірка

  2. \(m\) випадково вибрані предиктори (для розбиття)

Все інше про випадкові ліси працює так само, як і з bagging

Random forests в R

У вас є кілька варіантів для навчання випадкових лісів за допомогою tidymodels.
Наприклад, ranger, randomForest, spark.

rand_forest() отримує доступ до кожного з цих пакетів через їх двигуни.

  • Механізм за замовчуванням — «ranger» (пакет ranger).
  • Аргумент mtry дає \(m\), кількість предикторів при кожному розділенні.

Ви вже бачили інші гіперпараметри для ranger:

  • trees кількість дерев у випадковому лісі
  • min_n мін. к-ть спостережень

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
  • Три змінні на поділ
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
  • Три змінні на поділ
  • 100 дерев у лісі
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
  • Три змінні на поділ
  • 100 дерев у лісі
  • Принаймні 2 спостереж. на поділ
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
  • Три змінні на поділ
  • 100 дерев у лісі
  • Принаймні 2 спостереж. на поділ
  • Движок ranger
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Random forests в R

Навчання випадкового лісу в R за допомогою tidymodels…

… і ranger

  • Тип: Класифікація
  • Три змінні на поділ
  • 100 дерев у лісі
  • Принаймні 2 спостереж. на поділ
  • Движок ranger
  • Встановлення правило поділу
# Define the random forest
heart_rf = rand_forest(
  mode = "classification",
  mtry = 3,
  trees = 100,
  min_n = 2
) %>% set_engine(
  engine = "ranger",
  splitrule = "gini"
)

Крок 1: Визначте нашу сітку параметрів

# Define the parameter grid
rf_grid = expand_grid(
  mtry = 1:13,
  min_n = 1:15
)

Крок 2: Напишіть функцію, яка оцінює RF, використовуючи задані гіперпараметри.

# Function: One set of hyperparam
rf_i = function(i) {
  # Define the random forest
  heart_rf_i = rand_forest(
    mode = "classification", 
    mtry = rf_grid[i, 1],
    trees = 100,
    min_n = rf_grid[i, 2]
  ) %>% set_engine(engine = "ranger", splitrule = "gini")
  # Define workflow
  heart_rf_wf_i = 
    workflow() %>% add_model(heart_rf_i) %>% add_recipe(heart_recipe)
  # Fit
  heart_rf_fit_i = heart_rf_wf_i %>% fit(heart_df)
  # Return DF w/ OOB error and the hyperparameters
  return(tibble(
    mtry = rf_grid$mtry[i],
    min_n = rf_grid$min_n[i],
    # Note: OOB error is buried
    error_oob = heart_rf_fit_i$fit$fit$fit$prediction.error
  ))
}

Крок 3: Оцініть RF (parallel)!

# Fit the RFs on the grid
rf_tuning = future_map_dfr(
  1:nrow(rf_grid),
  rf_i
)

Точність (OOB) по сітці наших параметрів.

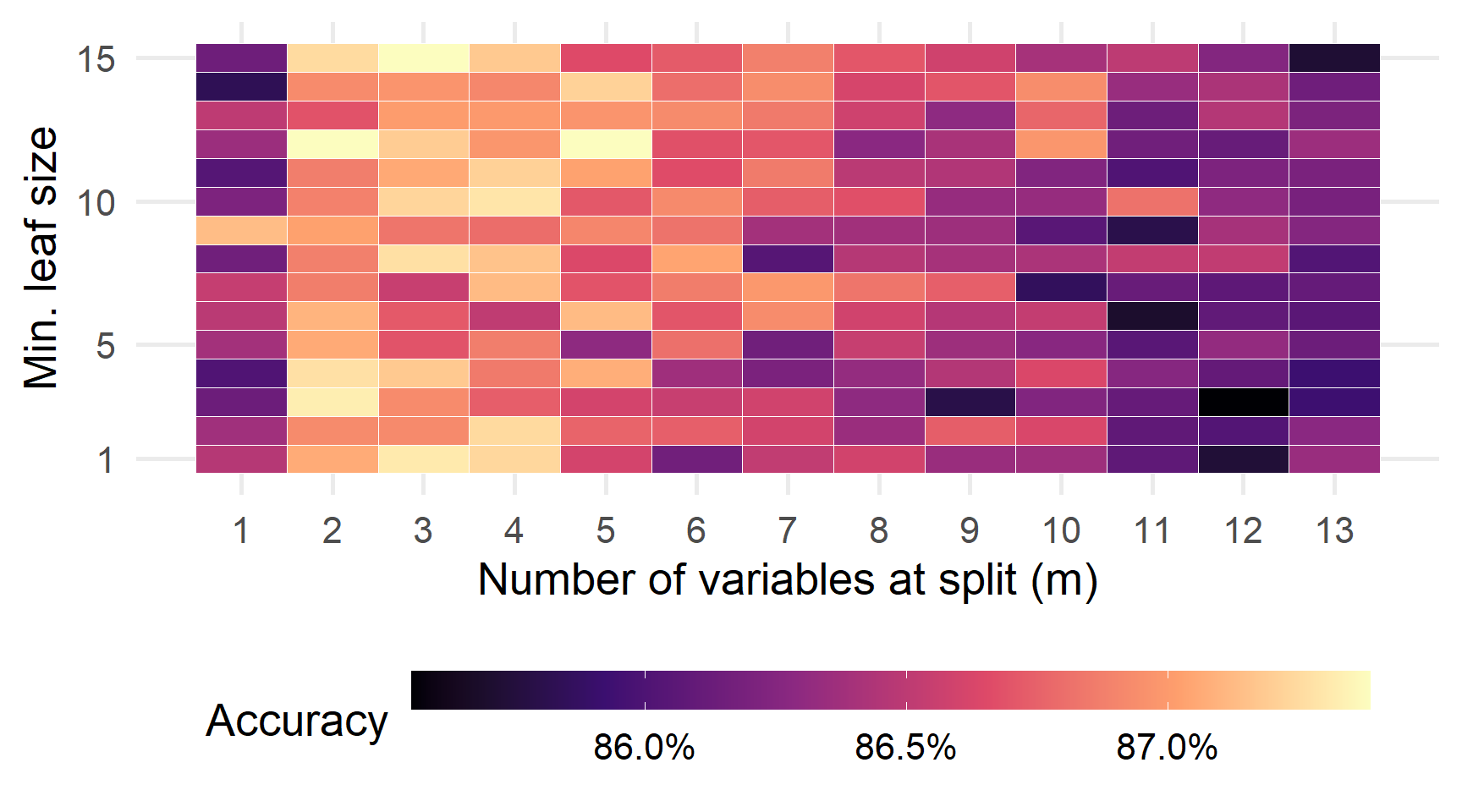
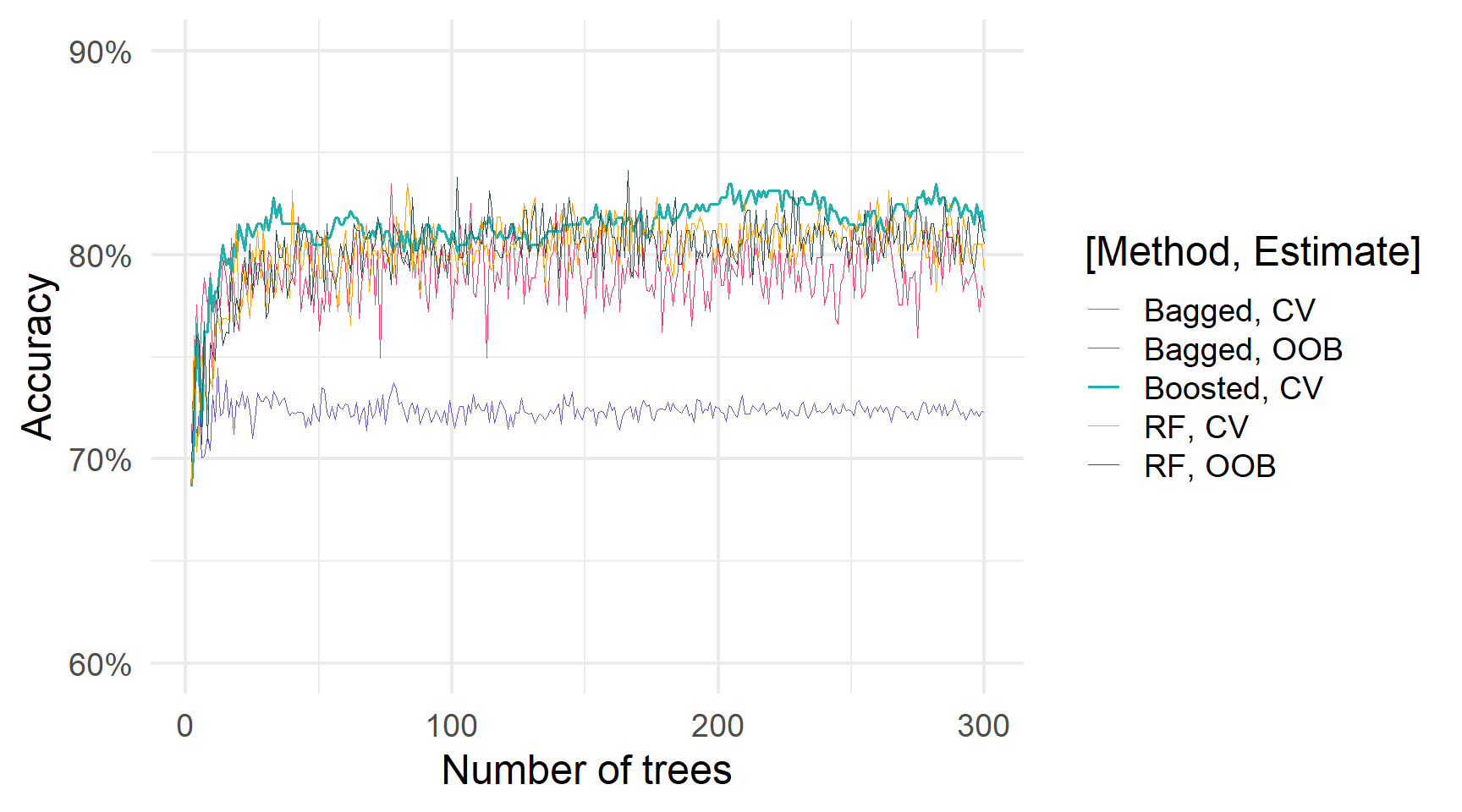
Ансамблі дерев і кількість дерев

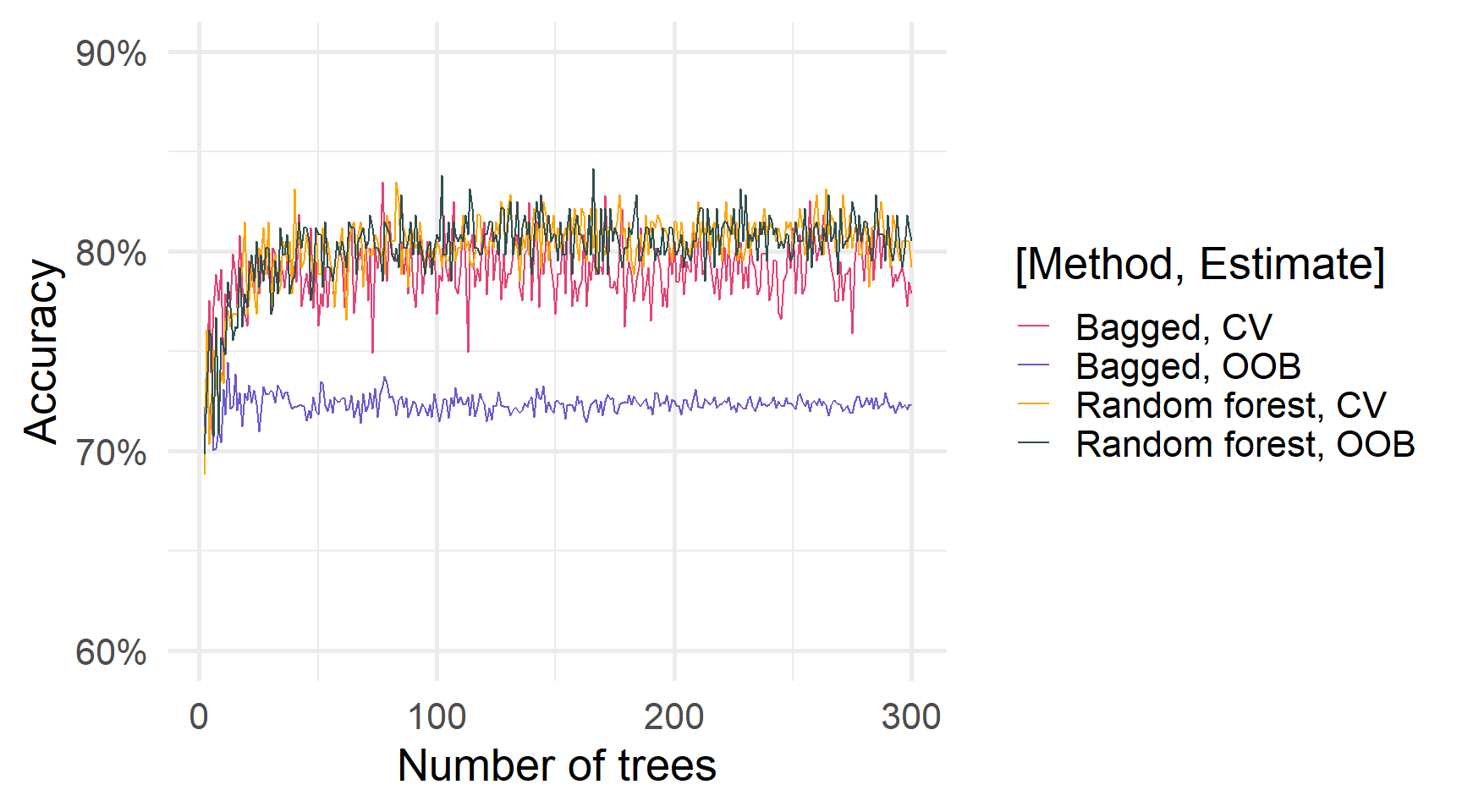
Boosting

Boosting

Поки що елементи наших ансамблів виступають самостійно:
жодне окреме дерево нічого не знає про решту лісу.

Boosting дозволяє деревам передавати інформацію одне одному.

Зокрема, boosting навчає свої дерева послідовно — кожне нове дерево тренується на залишках (помилках) своїх попередників.

  • Ми додаємо кожне нове дерево до нашої моделі \(\hat{f}\) (і оновлюємо наші залишки).

  • Дерева, як правило, невеликі — повільно покращують \(\hat{f}\).

Boosting

Boosting має три tuning параметри.

  1. Кількість дерев \(\color{#e64173}{B}\) може бути важливим для запобігання overfitting

2.Параметр зтиснення \(\color{#e64173}{\lambda}\), який контролює швидкість навчання бустінгу (часто 0,01 або 0,001).

  1. Кількість поділів \(\color{#e64173}{d}\) у кожному дереві (складність дерев).

  • Окремі дерева, як правило, короткі — часто \(d=1\) («пні»).

  • Пам’ятайте Дерева вчаться на помилках попередників,
    тому жодне дерево не має бути ідеальною моделлю.

How to boost

Крок 1: Установіть \(\color{#6A5ACD}{\mathop{\hat{f}}}(x) = 0\), що дає залишки \(r_i = y_i\) для всіх \(i\).

Крок 2: Для \(\color{#e64173}{b} = 1,\,2\,\ldots,\, B\) виконайте:

A. Підберіть дерево \(\color{#e64173}{\hat{f^b}}\) із розділенням \(d\).

B. Оновити модель \(\color{#6A5ACD}{\hat{f}}\) за допомогою «скороченої версії» нового дерева \(\color{#e64173}{\hat{f^b}}\)

\[ \begin{align} \color{#6A5ACD}{\mathop{\hat{f}}}(x) \leftarrow \color{#6A5ACD}{\mathop{\hat{f}}}(x) + \lambda \mathop{\color{#e64173}{\hat{f^b}}}(x) \end{align} \]

C. Оновіть залишки: \(r_i \leftarrow r_i - \lambda \mathop{\color{#e64173}{\hat{f^b}}}(x)\).

Крок 3: Виведіть розширену модель: \(\mathop{\color{#6A5ACD}{\hat{f}}}(x) = \sum_{b} \lambda \mathop{\color{#e64173}{\hat{f^b}}}(x)\).

Boosted residuals: розширення

Нагадування: Boosting trains - послідовні моделі \(\color{#e64173}{\hat{f_{i}}}(y,x)\) - на залишки попередніх моделей, \(\color{#FFA500}{r_{i-1}}\) (стиснуті на \(\color{#6A5ACD}{\lambda}\))

\[ \begin{align} \color{#FFA500}{r_0} &= y \\[1em] \color{#FFA500}{r_1} &= \color{#FFA500}{r_0} - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{1}}}(\color{#FFA500}{r_0}, x) \\[0.35em] &= y - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{1}}}(y, x) \\[1em] \color{#FFA500}{r_2} &= \color{#FFA500}{r_1} - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{2}}}(\color{#FFA500}{r_1}, x) \\[0.35em] &= y - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{1}}}(y, x) - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{2}}}(y - \color{#6A5ACD}{\lambda} \color{#e64173}{\hat{f_{1}}}(y, x), x) \\[1em] &\cdots \end{align} \]

Boosting in R

Ми будемо використовувати boost_tree() з parsnips для тренування boosting дерев1.

boost_tree() приймає кілька параметрів, які ви бачили, плюс ще один:

  1. mtry кількість предикторів для кожного розбиття
  2. дерева, кількість дерев \((B)\)
  3. min_n, мінімум спостережень для розділення
  4. tree_depth, макс. глибина дерева
  5. learn_rate, швидкість навчання \((\lambda)\)

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001),
    "n.minobsinnode" = 5
  )
)
  • boosted за допомогою пакету gbm

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001),
    "n.minobsinnode" = 5
  )
)
  • boosted за допомогою пакету gbm
  • перехресна перевірка (без OOB)

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001),
    "n.minobsinnode" = 5
  )
)
  • boosted за допомогою пакету gbm
  • перехресна перевірка (без OOB)
  • CV-пошук пошук по сітці
    • кількість дерев

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001),
    "n.minobsinnode" = 5
  )
)
  • boosted за допомогою пакету gbm
  • перехресна перевірка (без OOB)
  • CV-пошук пошук по сітці
    • кількість дерев
    • глибина дерева

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001), #<<
    "n.minobsinnode" = 5
  )
)
  • boosted за допомогою пакету gbm
  • перехресна перевірка (без OOB)
  • CV-пошук пошук по сітці
    • кількість дерев
    • глибина дерева
    • швидкість навчання

Boosting in R

# Set the seed
set.seed(12345)
# Train the random forest
heart_boost = train(
  heart_disease ~ .,
  data = heart_df,
  method = "gbm",
  trControl = trainControl(
    method = "cv",
    number = 5
  ),
  tuneGrid = expand.grid(
    "n.trees" = seq(25, 200, by = 25),
    "interaction.depth" = 1:3,
    "shrinkage" = c(0.1, 0.01, 0.001),
    "n.minobsinnode" = 5 #<<
  )
)
  • boosted за допомогою пакету gbm
  • перехресна перевірка (без OOB)
  • CV-пошук пошук по сітці
    • кількість дерев
    • глибина дерева
    • швидкість навчання
    • мінімальний розмір листка

Порівняння boosting параметрів — зверніть увагу на швидкість навчання

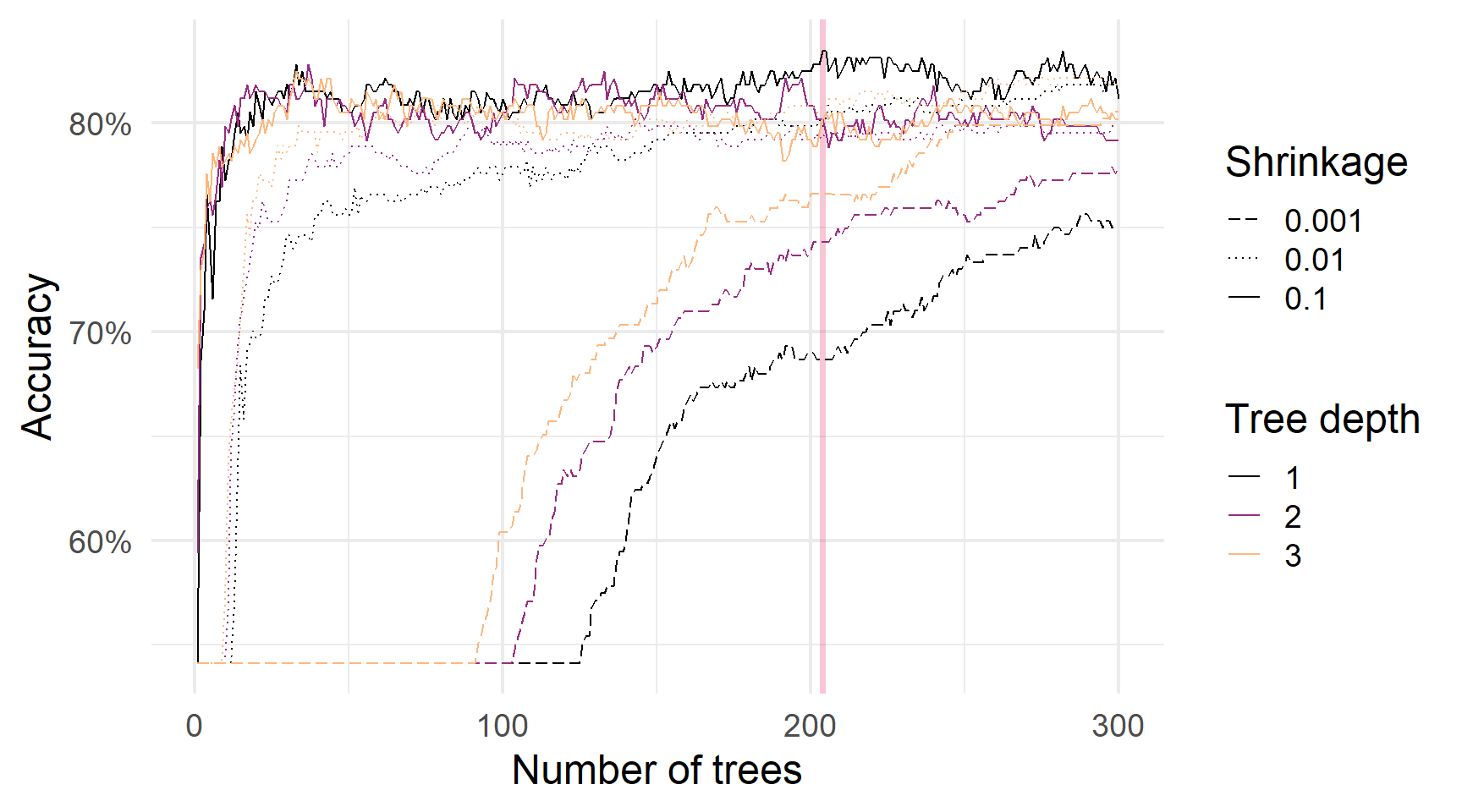
Порівняння boosting параметрів — більше дерев

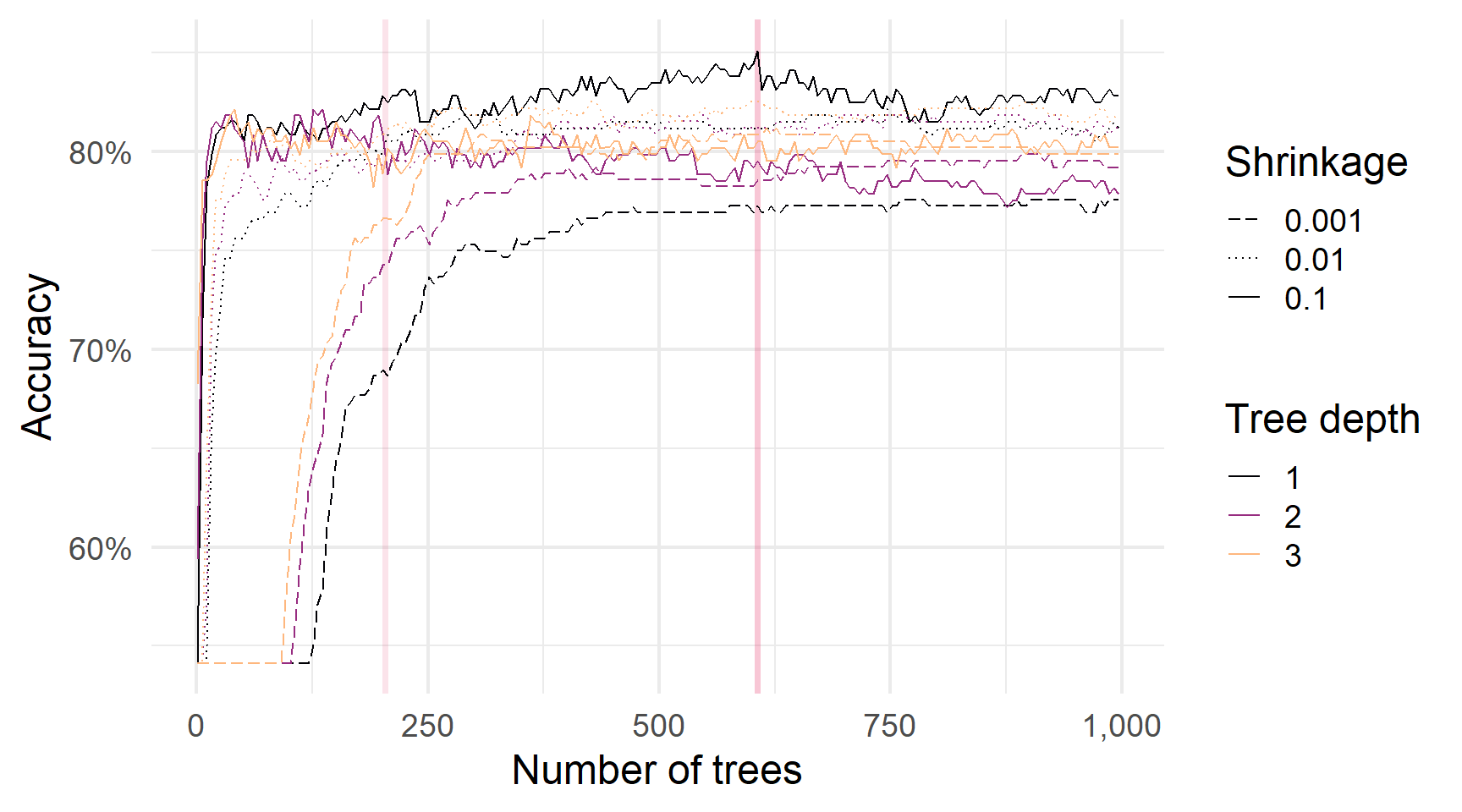
Порівняння boosting параметрів — ще більше дерев

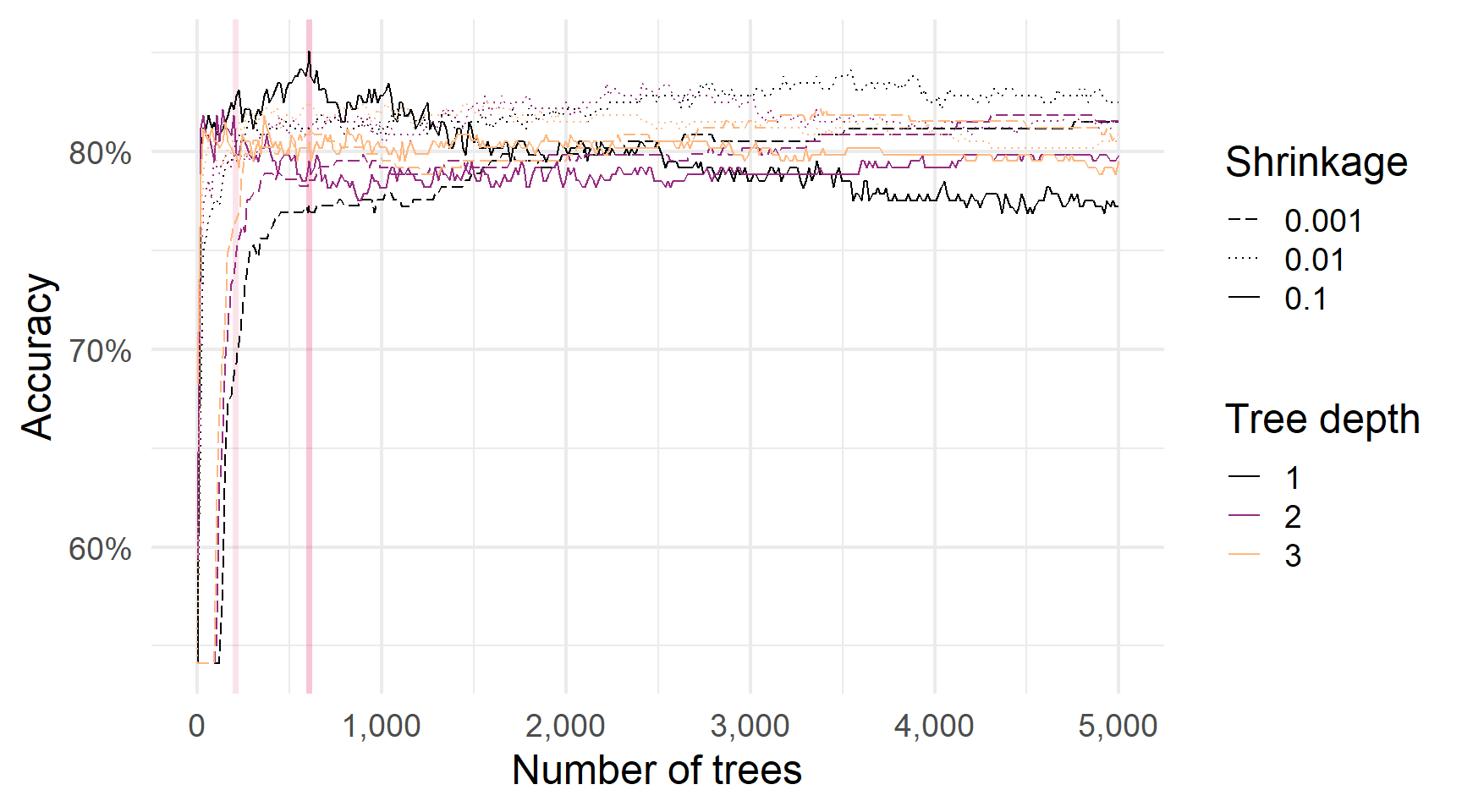
Порівняння boosting параметрів — і ще більше дерев

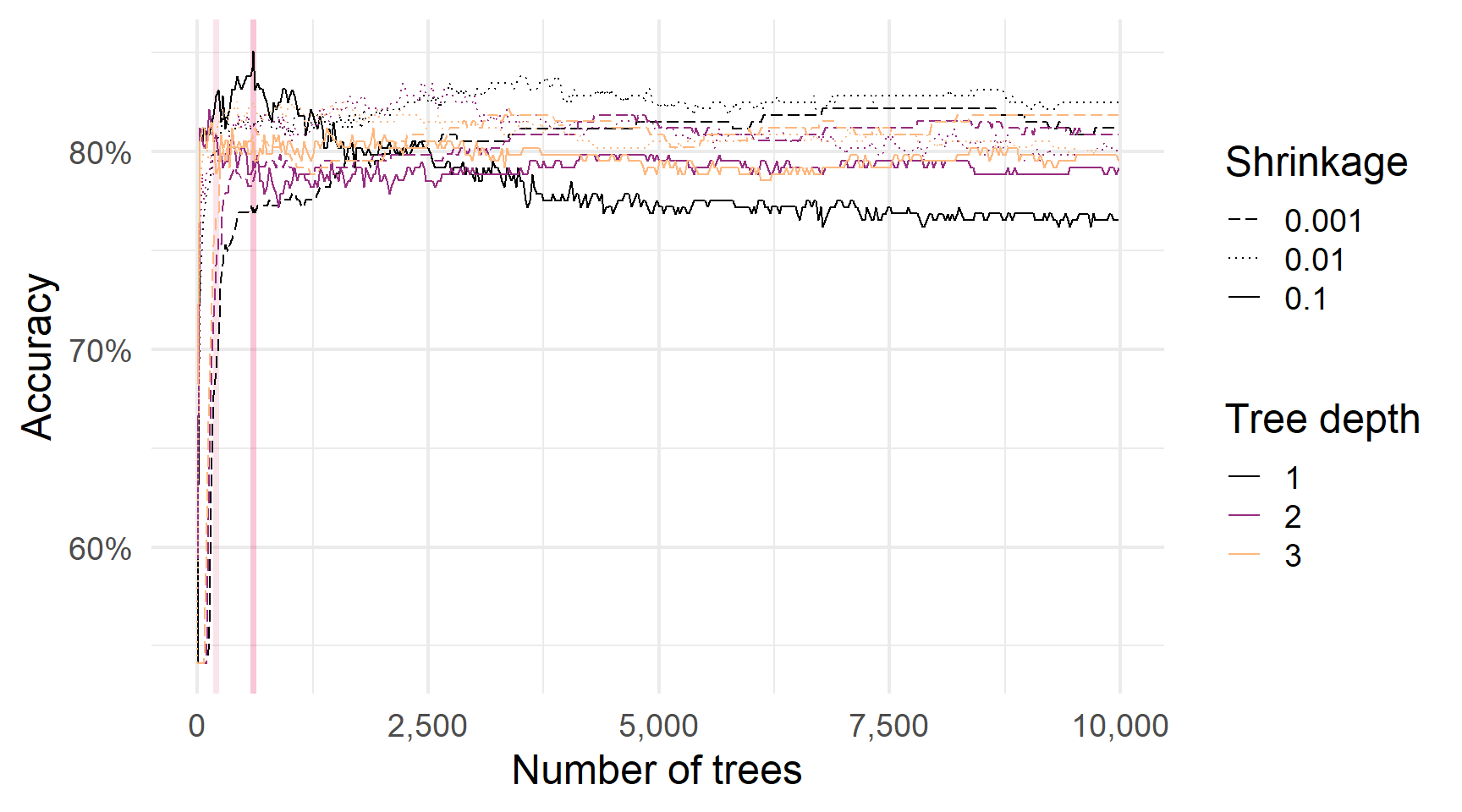
Ансамблі дерев та кількість дерев






Звичайно, є багато інших варіантів навчання на основі дерев:

Дякую за увагу!



Data Mirosh

@aranaur

ihor.miroshnychenko@kneu.ua

@ihormiroshnychenko

aranaur.rbind.io