04 - Відбір та регуляризація лінійних моделей

Machine Learning

Ігор Мірошниченко

КНЕУ::ІІТЕ

2023-03-20

Лінійна регресія

Лінійна регресія

Лінійна регресія «підбирає» коефіцієнти \(\color{#e64173}{\beta}_0,\, \ldots,\, \color{#e64173}{\beta}_p\) для моделі

\[ \begin{align} \color{#FFA500}{y}_i = \color{#e64173}{\beta}_0 + \color{#e64173}{\beta}_1 x_{1,i} + \color{#e64173}{\beta}_2 x_{2,i} + \cdots + \color{#e64173}{\beta}_p x_{p,i} + \varepsilon_i \end{align} \]

і часто застосовується в двох різних ситуаціях із досить різними цілями:

  1. Причинний висновок оцінює та інтерпретує коефіцієнти.

  2. Прогнозування фокусується на точному оцінюванні результатів.

Незалежно від мети, спосіб «підгонки» (оцінки) моделі однаковий.

Підгонка лінії регресії

Як і у випадку з багатьма методами навчання, регресія зосереджена на мінімізації певної міри втрати/помилки.

\[ \begin{align} e_i = \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \end{align} \]

У лінійній регресії використовується функція втрат L2, яка також називається сума квадратів помилок (SSE) або залишкова сума квадратів (RSS)

\[ \begin{align} \text{RSS} = e_1^2 + e_2^2 + \cdots + e_n^2 = \sum_{i=1}^n e_i^2 \end{align} \]

Зокрема: OLS вибирає \(\color{#e64173}{\hat{\beta}_j}\), який мінімізує RSS.

Ефективність

Існує велика різноманітність способів оцінки моделей лінійної регресії.

Residual standard error (RSE) \[ \begin{align} \text{RSE}=\sqrt{\dfrac{1}{n-p-1}\text{RSS}}=\sqrt{\dfrac{1}{n-p-1}\sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2} \end{align} \]

R-квадрат \[ \begin{align} R^2 = \dfrac{\text{TSS} - \text{RSS}}{\text{TSS}} = 1 - \dfrac{\text{RSS}}{\text{TSS}} \quad \text{де} \quad \text{TSS} = \sum_{i=1}^{n} \left( y_i - \overline{y} \right)^2 \end{align} \]

Ефективність і перенавчання

R2 не забезпечує захисту від перенавчання, а насправді тільки сприяє йому. \[ \begin{align} R^2 = 1 - \dfrac{\text{RSS}}{\text{TSS}} \end{align} \] Додавання нових змінних: RSS \(\downarrow\) і TSS не змінено. Таким чином, R2 збільшується.

RSE трохи штрафує додаткові змінні: \[ \begin{align} \text{RSE}=\sqrt{\dfrac{1}{n-p-1}\text{RSS}} \end{align} \] Додавання нових змінних: RSS \(\downarrow\), але \(p\) збільшується.

Приклад
Давайте подивимося, як працюють R2 і RSE з 500 дуже слабкими предикторами.

R2 на навчальній вибірці постійно збільшується, коли ми додаємо предиктори.
R2 на тестовій вибірці - ні.

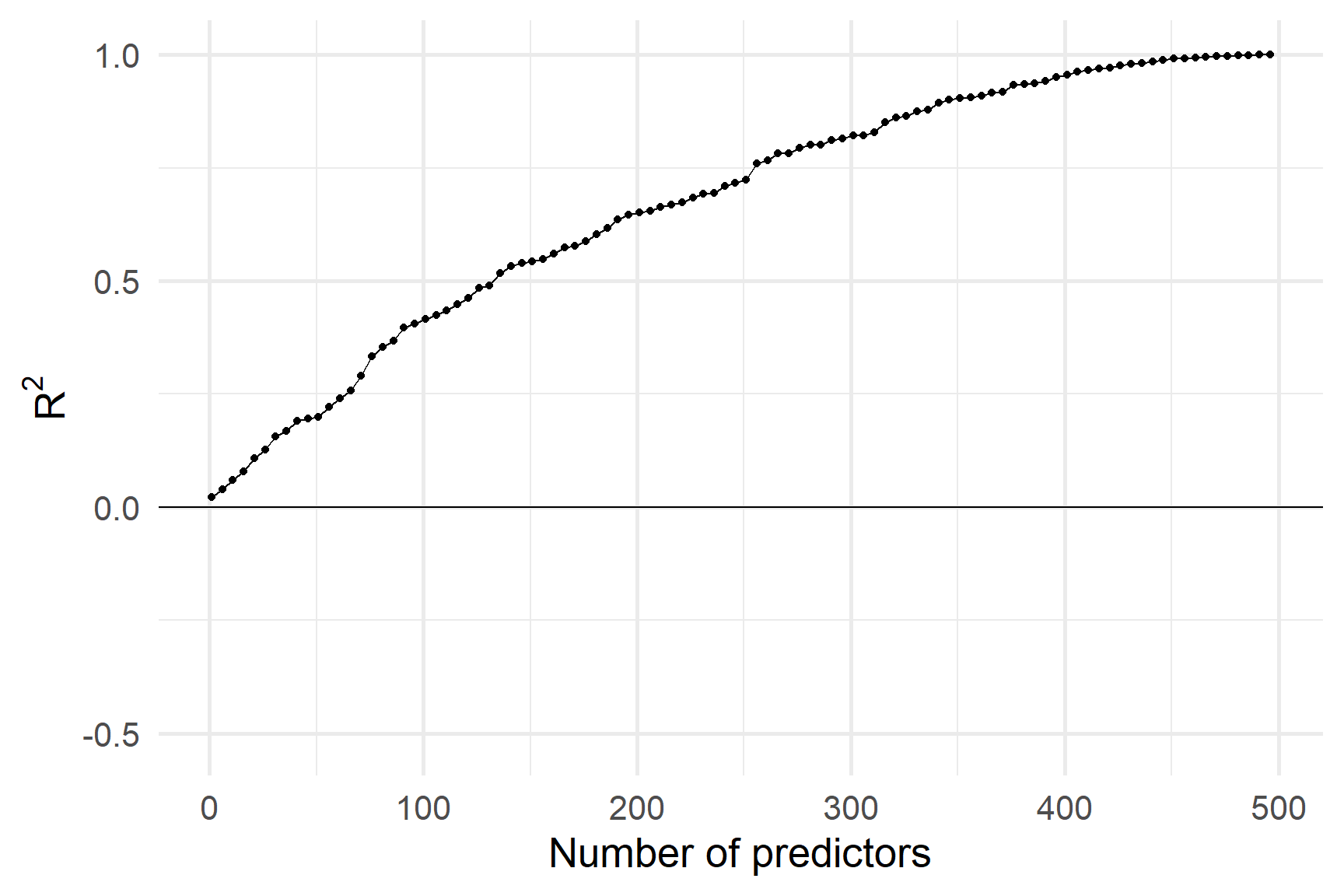
R2 на навчальній вибірці постійно збільшується, коли ми додаємо предиктори.
R2 на тестовій вибірці - ні.

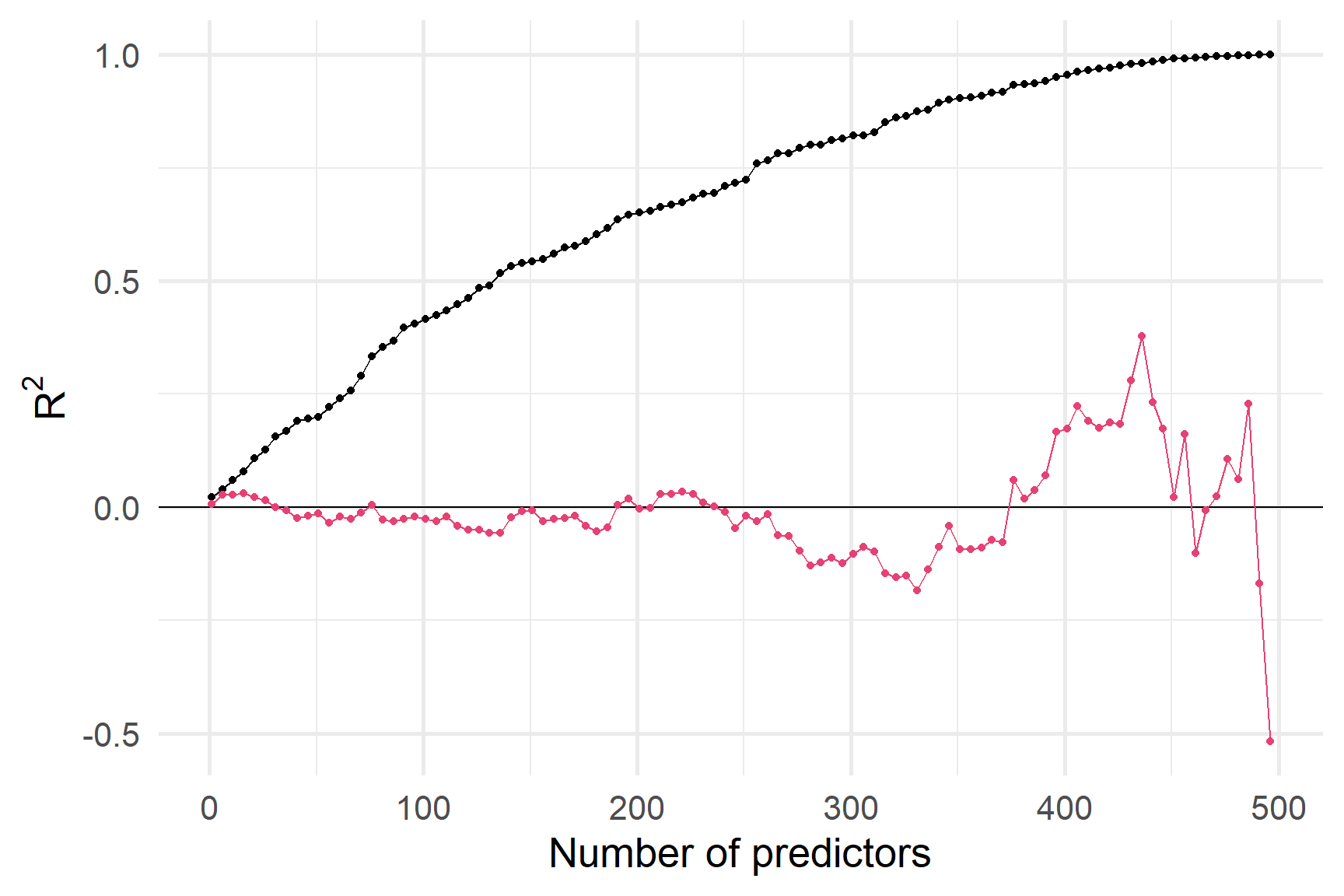
А як щодо RSE? Чи допомагає його штраф?

Незважаючи на штраф за додавання змінних, RSE на навчальній вибірці все ще може бути надмірним,
про що свідчить RSE на тестовій вибірці

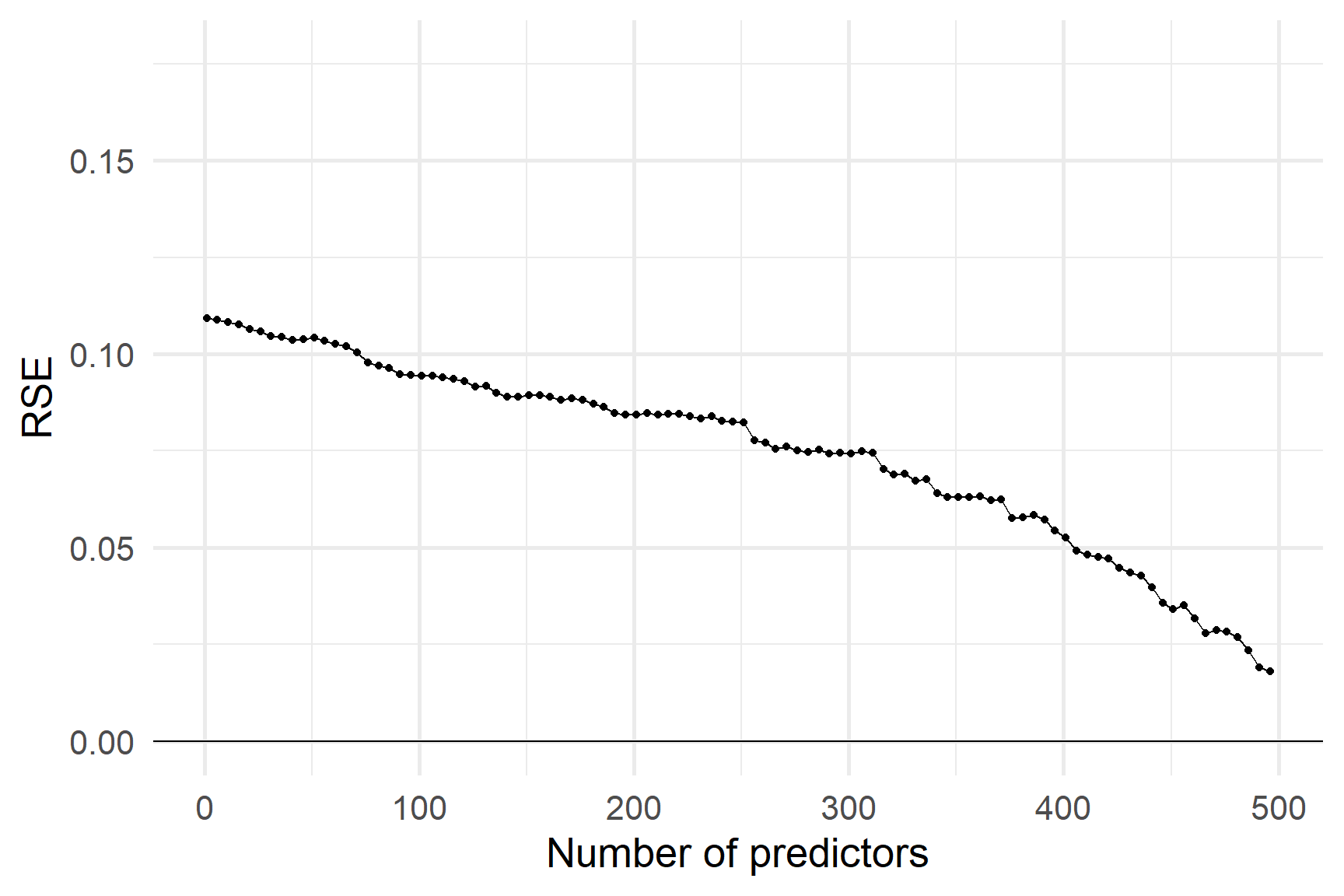
Незважаючи на штраф за додавання змінних, RSE на навчальній вибірці все ще може бути надмірним,
про що свідчить RSE на тестовій вибірці

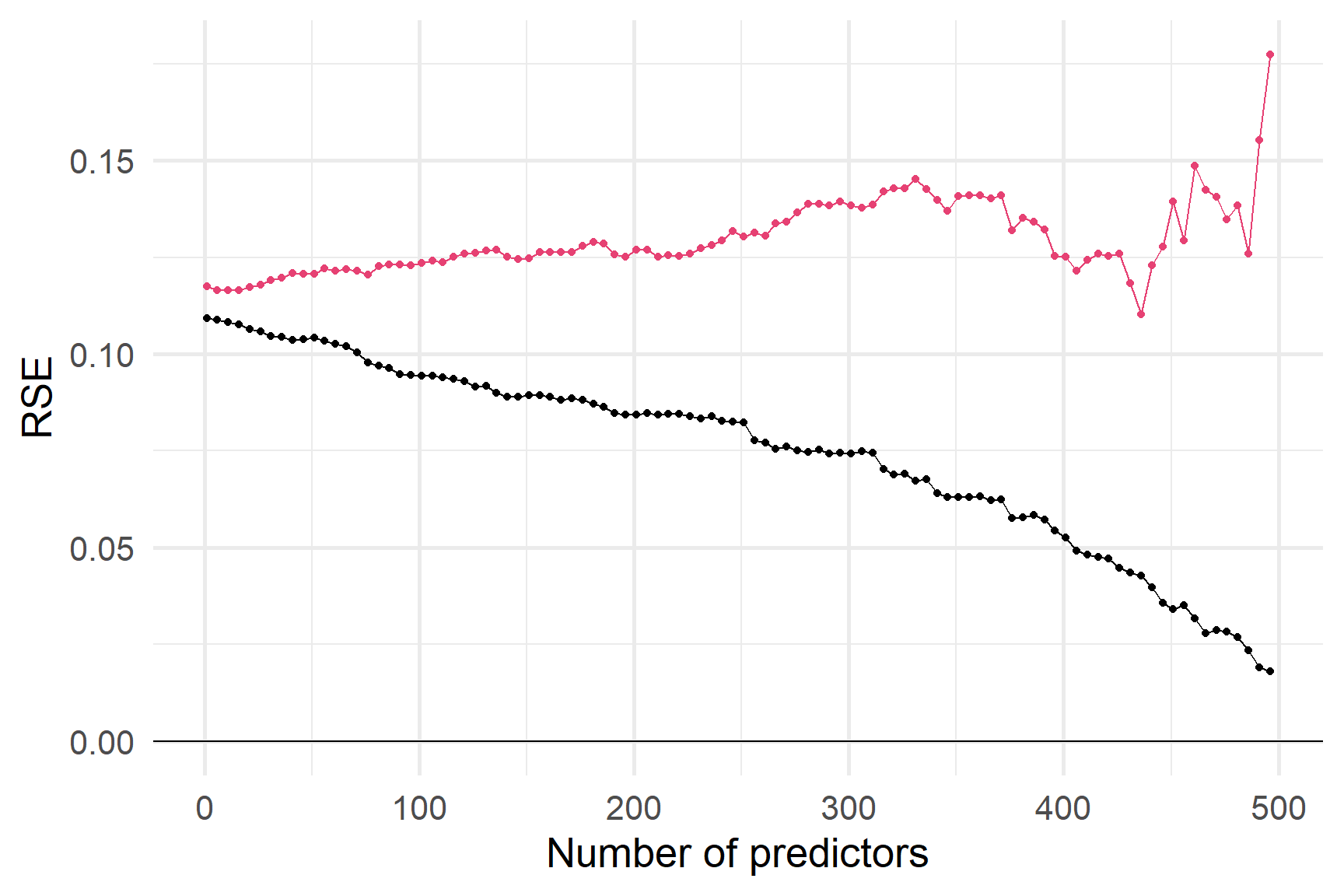
Пенальті

RSE — не єдиний спосіб штрафувати за додавання змінних.

Adjusted R2 — ще одне класичне рішення.

\[ \begin{align} \text{Adjusted }R^2 = 1 - \dfrac{\text{RSS}\color{#6A5ACD}{/(n - p - 1)}}{\text{TSS}\color{#6A5ACD}{/(n-1)}} \end{align} \]

Adj. R2 намагається “виправити” R2 за допомогою додавання штрафу за кількість змінних.

  • \(\text{RSS}\) завжди зменшується, коли додається нова змінна.
  • \(\color{#6A5ACD}{\text{RSS}/(n-p-1)}\) може збільшуватися або зменшуватися з новою змінною.

Однак in-sample adjusted R2 все ще може бути перенавчаним.
Ілюстровано out-of-sample R2

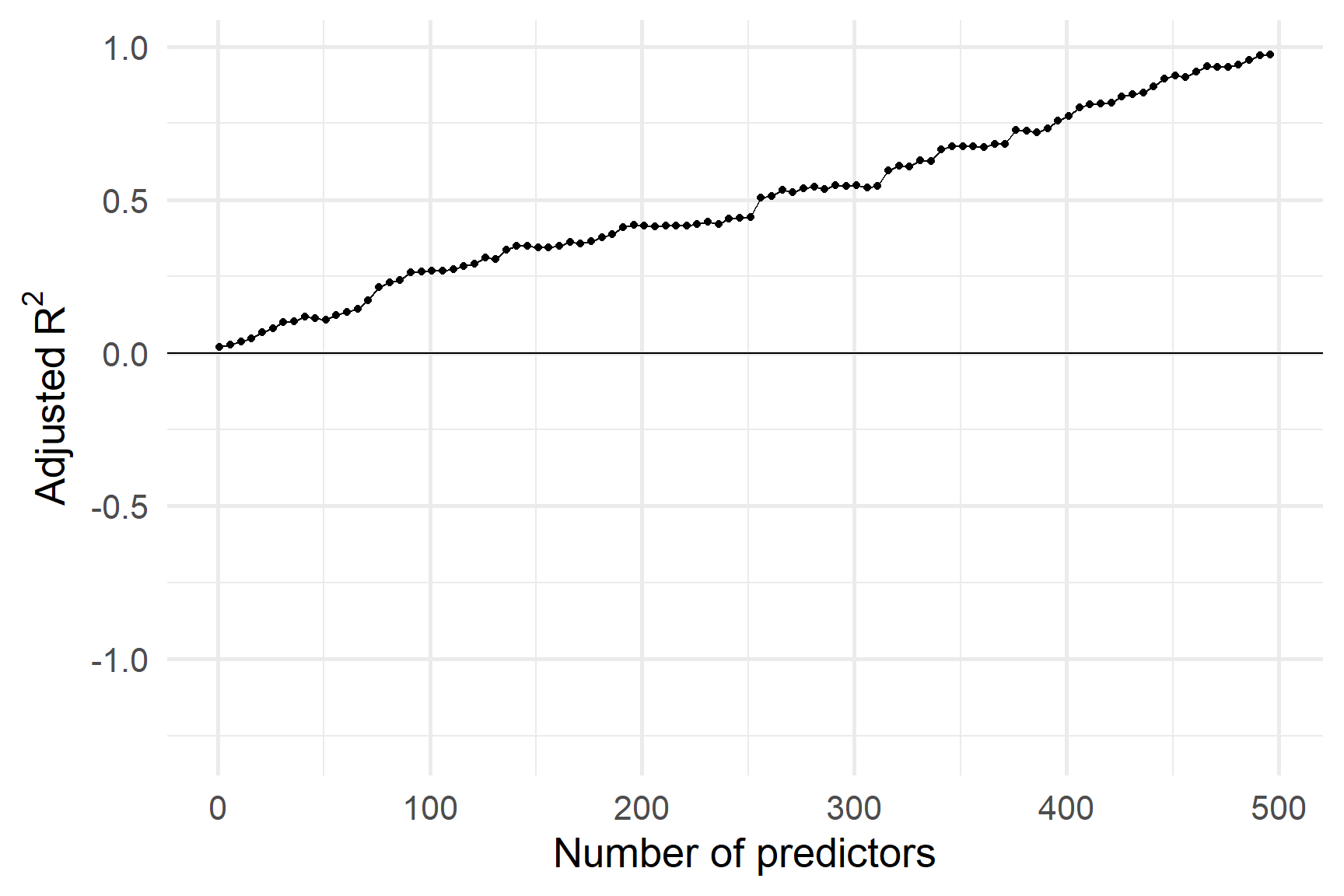
Однак in-sample adjusted R2 все ще може бути перенавчаним.
Ілюстровано out-of-sample R2

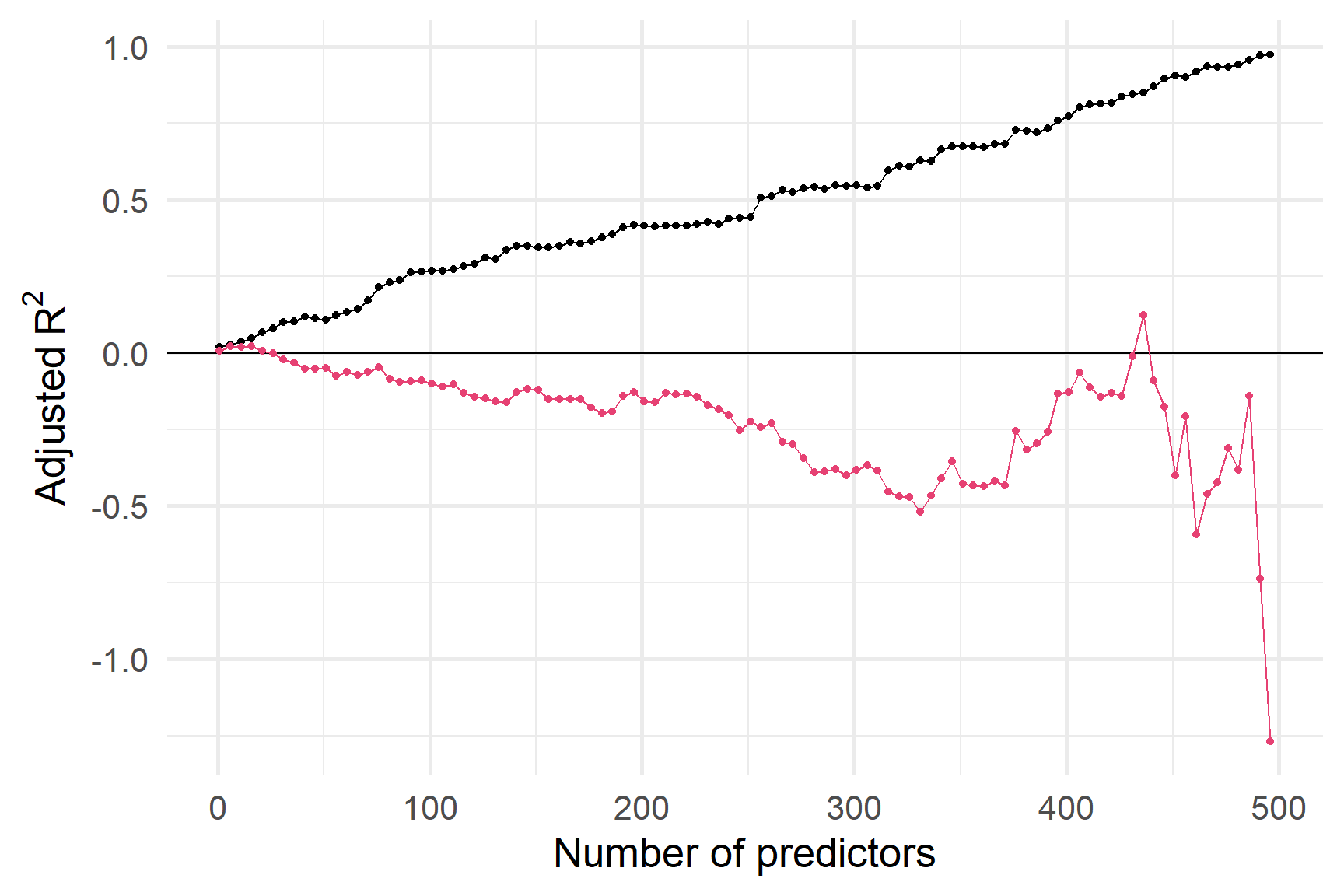
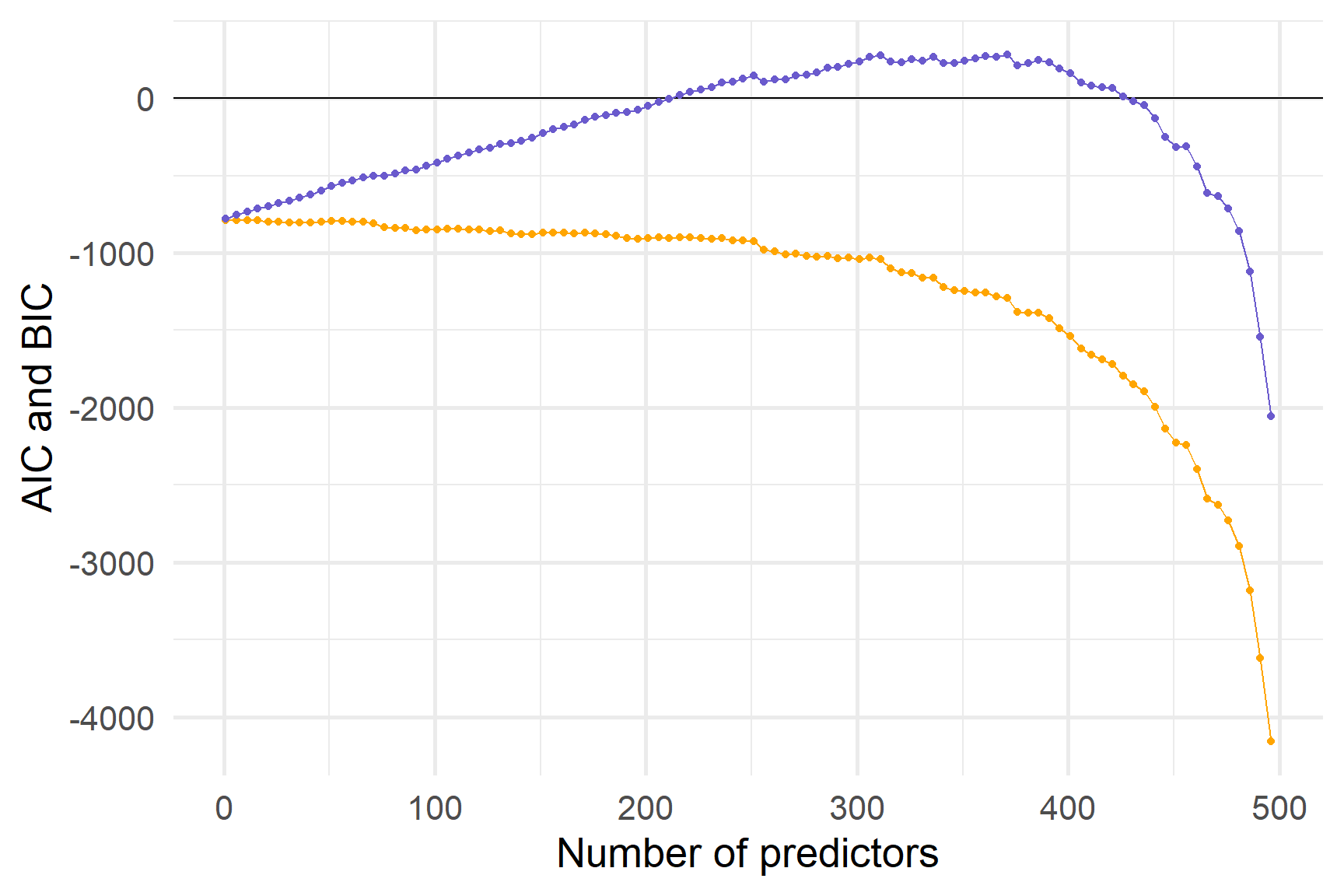
Ось in-sample AIC і BIC.
Здається, жодна метрика у вибірці не захищає повністю від перенавчання.

Кращий спосіб?

R2, скоригований R2 і RSE кожен пропонує певний відтінок підгонки моделі, але вони здаються обмеженими у своїх можливостях запобігати перенавчанню.

Ми хочемо, щоб був метод оптимального вибору (лінійної) моделі — збалансування дисперсії та зміщення та уникнення перенавчання

Сьогодні ми обговоримо два (пов’язані) методи:

  1. Вибір підмножини вибирає (під)множину наших \(p\) предикторів

  2. Використання всіх \(p\) предикторів для оцінки моделі.

Вибір підмножини

Вибір підмножини

При виборі підмножини ми:

  1. Скоротити потенційні предиктори \(p\) (за допомогою магії/алгоритму)
  2. Оцінити обрану лінійну модель за допомогою МНК

Як ми можемо скоротити кількість предикторів?

  • Вибір найкращої підмножини: оцінити моделі для кожної можливої підмножини.
  • Forward stepwise selection починається лише з intercept та намагається створити найкращу модель (використовуючи певний критерій відповідності).
  • Backward stepwise selection починається з усіх змінних \(p\) і намагається відкинути змінні, поки не досягне найкращої моделі (використовуючи певний критерій відповідності).
  • Гібридні підходи

Вибір найкращої підмножини

Вибір найкращої підмножини базується на простій ідеї: оцінити модель для кожної можливої підмножини змінних; потім порівняйте їхні результати.

Але…

«Модель для кожної можливої підмножини» може означати багато \(\left( 2^p \right)\) моделей.

Дуже багато моделей…

  • 10 предикторів \(\rightarrow\) 1024 моделі для підгонки
  • 25 предикторів \(\rightarrow\) >33,5 мільйонів моделей для підгонки
  • 100 предикторів \(\rightarrow\) ~1,5 трильйона моделей для підгонки

Навіть маючи велику кількість дешевої обчислювальної потужності, ми можемо зіткнутися з проблемами.

Вибір найкращої підмножини

Алгоритм:

  1. Визначте \(\mathcal{M}_0\) як модель без предикторів.

  2. Для \(k\) від 1 до \(p\):

    • Підбирайте всі можливі моделі за допомогою \(k\) предикторів.

    • Визначте \(\mathcal{M}_k\) як “найкращу” модель з \(k\) предикторами.

  3. Виберіть “найкращу” модель із \(\mathcal{M}_0,\,\ldots,\,\mathcal{M}_p\).

Як ми бачили, RSS знижується (а R2 збільшується) з \(p\), тому ми повинні використовувати крос-валідацію.

Притклад dataset: Credit

Ми будемо використовувати набір даних Credit з пакета R ISLR.

Набір даних Credit містить 400 спостережень щодо 12 змінних.

Притклад dataset: Credit

Нам потрібно попередньо обробити набір даних, перш ніж ми зможемо вибрати модель…

Тепер набір даних містить 400 спостереження щодо 12 змінних (2048 підмножин).

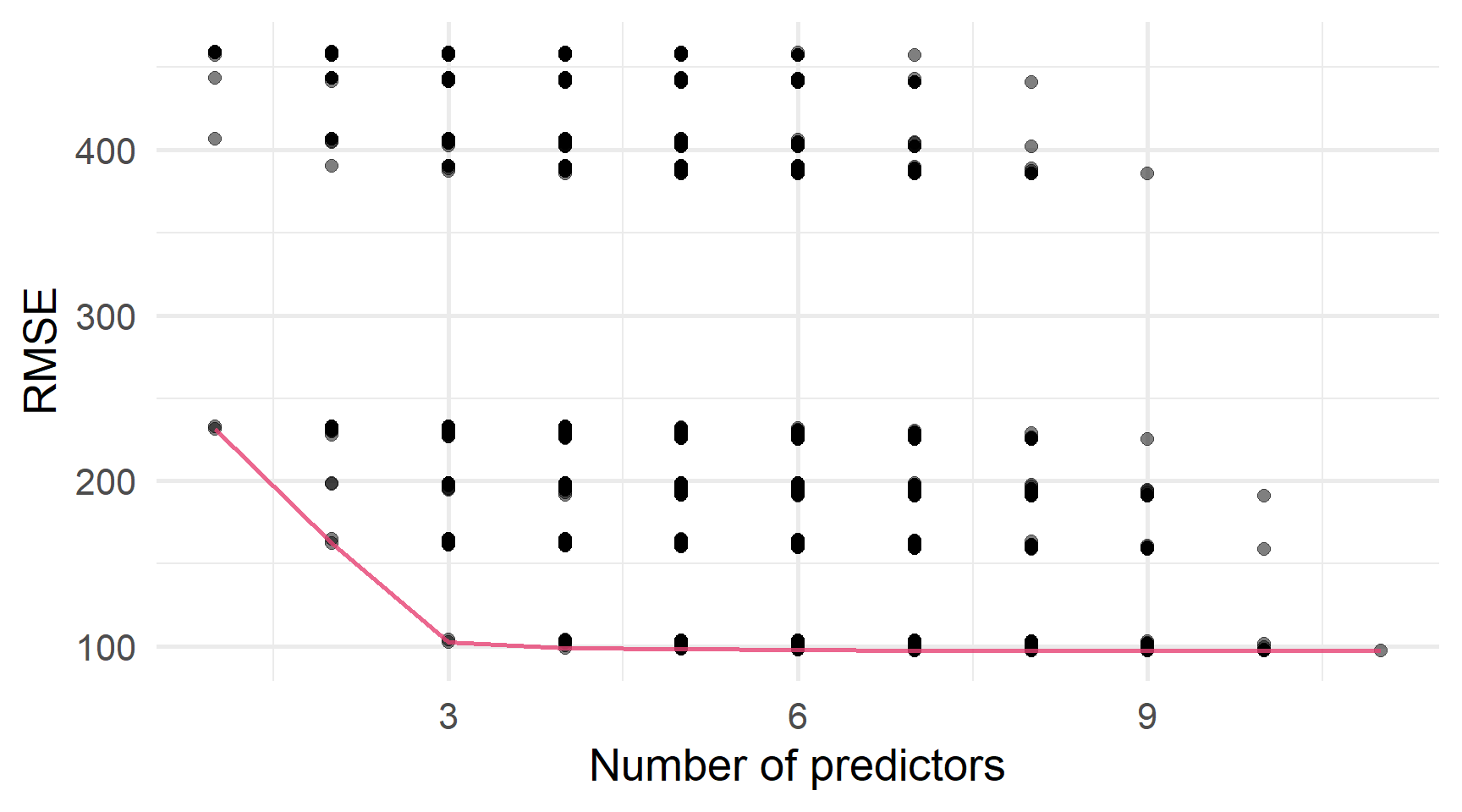
Вибір найкращої підмножини

Звідси:

  1. Оцініть помилку крос-валідації для кожного \(\mathcal{M}_k\).

  2. Виберіть \(\mathcal{M}_k\), які мінімізують помилку CV.

  3. Навчіть обрану модель на повному наборі даних.

Вибір найкращої підмножини

Попередження

  • Обчислювально інтенсивний
  • Вибрані моделі можуть бути «неправильними»
  • Вам потрібно захиститися від перенавчання під час вибору \(\mathcal{M}_k\)
  • Також слід хвилюватися про перенавчання, коли \(p\) “великий”
  • Залежність від змінних.

Переваги

  • Комплексний пошук за наданими змінними
  • Результуюча модель — якщо її оцінити за допомогою OLS — має властивості OLS
  • Можна застосовувати до інших (не OLS) оцінювачів

Stepwise selection

Stepwise selection надає менш обчислювальну альтернативу вибору найкращої підмножини.

Основна ідея:

  1. Почніть з довільної моделі.
  2. Спробуйте знайти «кращу» модель, додаючи/вилучаючи змінні.
  3. Повторіть.
  4. Зупиніться, коли у вас буде найкраща модель. (Або виберіть найкращу модель.)

Два найпоширеніших різновиди ступінчастого відбору: - Forward починається лише з intercept \(\left( \mathcal{M}_0 \right)\) і додає змінні - Backward починається з усіх змінних \(\left( \mathcal{M}_p \right)\) і видаляє змінні

Forward stepwise

  1. Почніть з моделі лише з intercept (без предикторів), \(\mathcal{M}_0\).

  2. Для \(k=0,\,\ldots,\,p\):

    • Оцініть модель для кожного з решти предикторів \(p-k\), окремо додавши предиктори до моделі \(\mathcal{M}_k\).

    • Визначте \(\mathcal{M}_{k+1}\) як «найкращу» модель з моделей \(p-k\).

  3. Виберіть «найкращу» модель із \(\mathcal{M}_0,\,\ldots,\, \mathcal{M}_p\).

Forward stepwise з caret в R

train_forward = train(
  y = credit_dt[["balance"]],
  x = credit_dt %>% dplyr::select(-balance),
  trControl = trainControl(method = "cv", number = 5),
  method = "leapForward",
  tuneGrid = expand.grid(nvmax = 1:11)
)

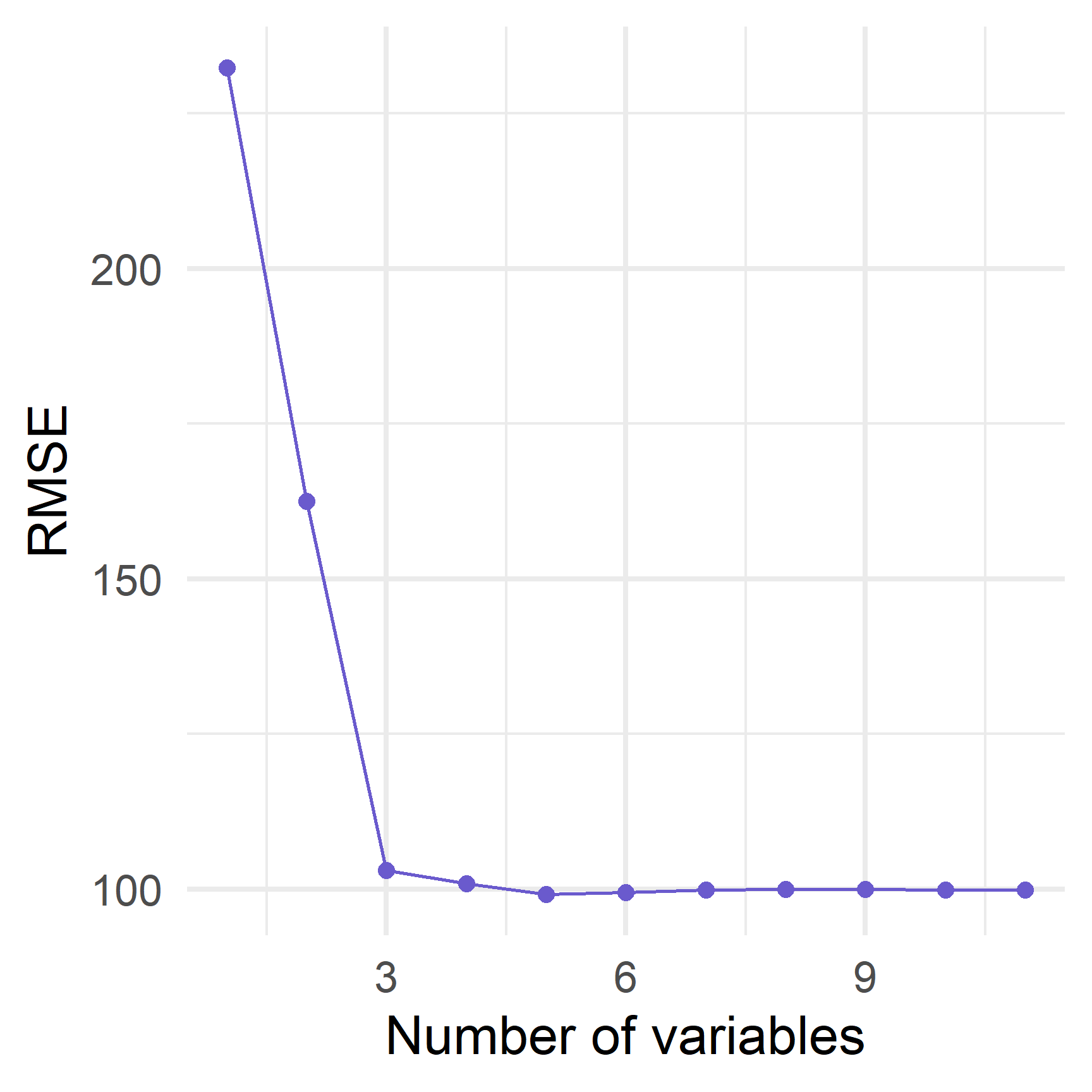
Backward stepwise

Алгоритм:

  1. Почніть з моделі, яка включає всі \(p\) предиктори: \(\mathcal{M}_p\).

  2. Для \(k=p,\, p-1,\, \ldots,\,1\):

    • Оцінка \(k\) моделей, де кожна модель вилучає один із \(k\) предикторів з \(\mathcal{M}_k\).

    • Визначте \(\mathcal{M}_{k-1}\) як “найкращу” з моделей \(k\).

  3. Виберіть «найкращу» модель із \(\mathcal{M}_0,\,\ldots,\, \mathcal{M}_p\).

Backward stepwise з caret в R

train_backward = train(
  y = credit_dt[["balance"]],
  x = credit_dt %>% dplyr::select(-balance),
  trControl = trainControl(method = "cv", number = 5),
  method = "leapBackward",
  tuneGrid = expand.grid(nvmax = 1:11)
)

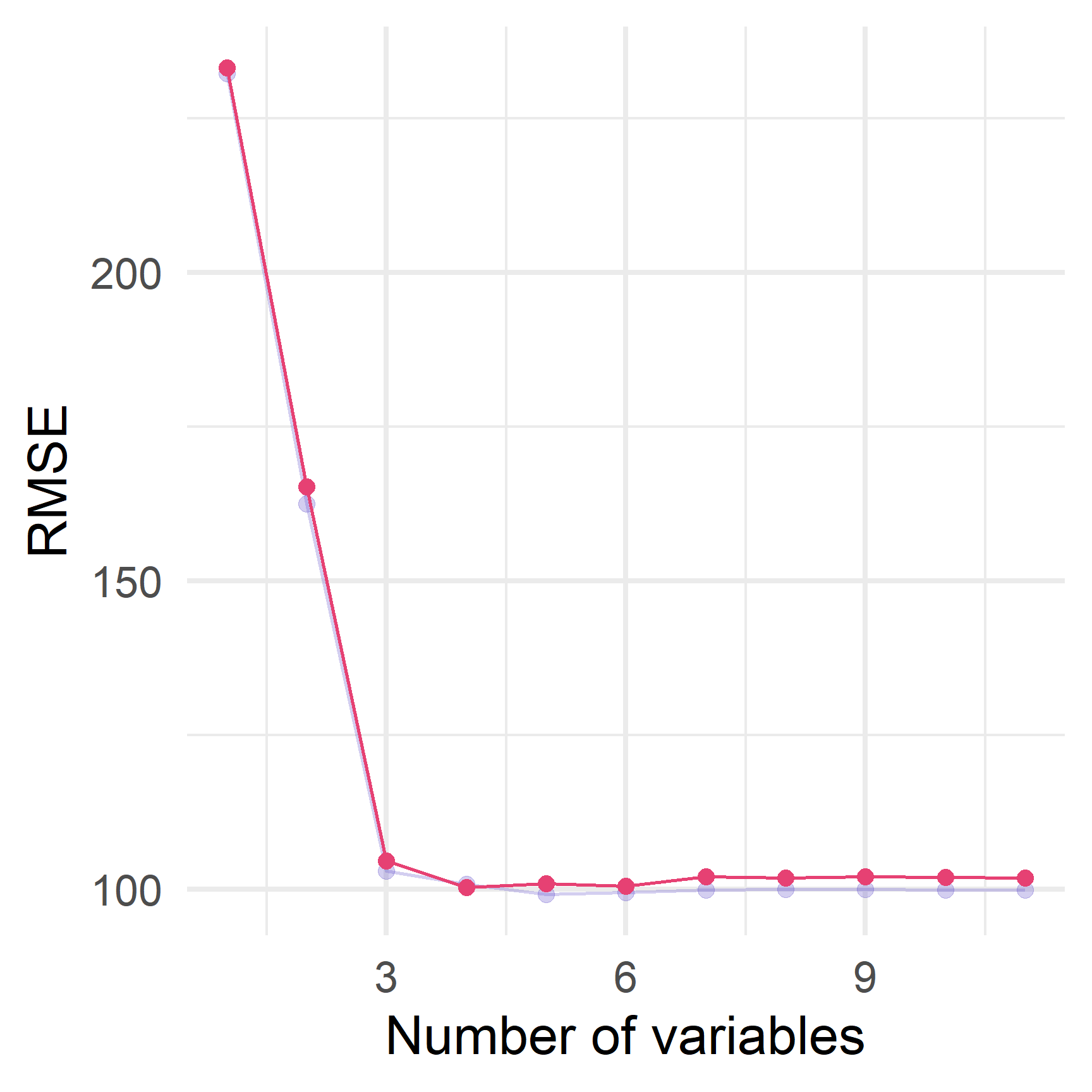
Forward and Backward step. selection можуть вибрати різні моделі.

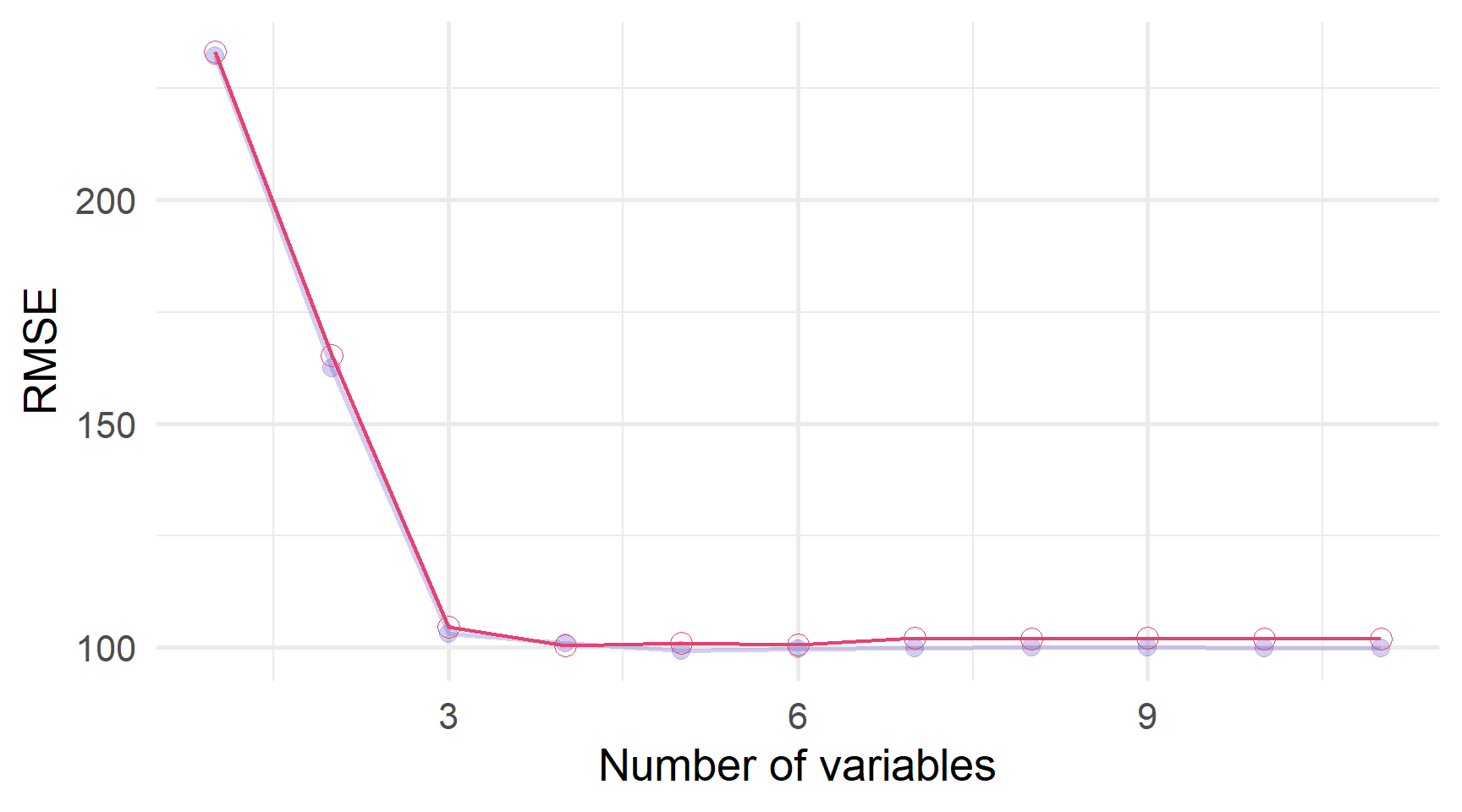
Критерії

Яку модель ви виберете, залежить від того, як ви визначаєте “найкращу модель”.

І у нас є багато варіантів…

Ми бачили RSS, (R)MSE, RSE, R2, Adj. R2.

Звичайно, є так звані інформаційні критерії, які сильніше штрафують модель за \(d\) предикторів.

\[ \begin{align} C_p &= \frac{1}{n} \left( \text{RSS} + \color{#6A5ACD}{2 d \hat{\sigma}^2 }\right) \\[1ex] \text{AIC} &= \frac{1}{n\hat{\sigma}^2} \left( \text{RSS} + \color{#6A5ACD}{2 d \hat{\sigma}^2 }\right) \\[1ex] \text{BIC} &= \frac{1}{n\hat{\sigma}^2} \left( \text{RSS} + \color{#6A5ACD}{\log(n) d \hat{\sigma}^2 }\right) \end{align} \]

Регуляризація

Регуляризація

Це потужна альтернатива “підвибірки”.

  • оцінює модель, яка містить всі \(\color{#e64173}{p}\) предиктори.
  • одночасно: стискає (штрафує) коефіцієнти до нуля

Регуляризація

  • Зменшення наших коефіцієнтів до нуля зменшує дисперсію моделі
  • Штрафує нашу модель за великів коефіцієнти та стискає їх до нуля.
  • Оптимальний штраф збалансує дисперсію та зміщення.

Тепер ви розумієте методи регуляризації:

  • Ridge regression
  • Lasso
  • Elasticnet

Ridge regression

Ridge regression

Назад до МНК (знову)

Регресія найменших квадратів отримує \(\hat{\beta}_j\) шляхом мінімізації RSS, тобто, \[ \begin{align} \min_{\hat{\beta}} \text{RSS} = \min_{\hat{\beta}} \sum_{i=1}^{n} e_i^2 = \min_{\hat{\beta}} \sum_{i=1}^{n} \bigg( \color{#FFA500}{y_i} - \color{#6A5ACD}{\underbrace{\left[ \hat{\beta}_0 + \hat{\beta}_1 x_{i,1} + \cdots + \hat{\beta}_p x_{i,p} \right]}_{=\hat{y}_i}} \bigg)^2 \end{align} \]

Ридж регресія вносить невеликі зміни:

  • додає штраф = сума квадратів коефіцієнтів \(\left( \color{#e64173}{\lambda\sum_{j}\beta_j^2} \right)\)
  • мінімізує (зважену) суму RSS і штрафу

\[ \begin{align} \min_{\hat{\beta}^R} \sum_{i=1}^{n} \bigg( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \bigg)^2 + \color{#e64173}{\lambda \sum_{j=1}^{p} \beta_j^2} \end{align} \]

Ridge regression

Ridge regression \[ \begin{align} \min_{\hat{\beta}^R} \sum_{i=1}^{n} \bigg( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \bigg)^2 + \color{#e64173}{\lambda \sum_{j=1}^{p} \beta_j^2} \end{align} \]

Least squares \[ \begin{align} \min_{\hat{\beta}} \sum_{i=1}^{n} \bigg( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \bigg)^2 \end{align} \]

\(\color{#e64173}{\lambda}\enspace (\geq0)\) — це параметр налаштування сили штрафу.
\(\color{#e64173}{\lambda} = 0\) не передбачає штрафу: ми повернулися до методу найменших квадратів.

Кожне значення \(\color{#e64173}{\lambda}\) створює новий набір коефіцієнтів.

Ridge regression до компромісу зміщення та дисперсії: баланс

  • зменшення RSS, тобто, \(\sum_i\left( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \right)^2\)
  • зменшення коефіцієнтів (ігноруємо intecept)

Ridge regression

\(\lambda\) і штраф

Ключовим є вибір значення для \(\lambda\).

  • Якщо \(\lambda\) занадто мала, то наша модель повертається до OLS.
  • Якщо \(\lambda\) занадто велика, ми скорочуємо всі наші коефіцієнти занадто близько до нуля.

Що робити?

Викорисовувати крос-валідацію.

Штраф

Оскільки ми підсумовуємо квадрат коефіцієнтів, ми штрафуємо більші коефіціенти набагато більше, ніж збільшення малих коефіцієнтів.

Приклад За значення \(\beta\) ми платимо штраф у \(2 \lambda \beta\) за невелике збільшення.

  • При \(\beta = 0\) штраф за невелике збільшення становить \(0\).
  • При \(\beta = 1\) штраф за невелике збільшення становить \(2\lambda\).
  • При \(\beta = 2\) штраф за невелике збільшення становить \(4\lambda\).
  • При \(\beta = 3\) штраф за невелике збільшення становить \(6\lambda\).
  • При \(\beta = 10\) штраф за невелике збільшення становить \(20\lambda\).

Штрафи та стандартизація

Значення предикторів можуть мати суттєвий вплив на результат рідж регресії

Чому?

Тому що значення \(\mathbf{x}_j\) впливають на \(\beta_j\), а ridge дуже чутливий до \(\beta_j\).

Приклад Нехай \(x_1\) це відстань.

МНК
Якщо \(x_1\) вимірюється метрами і \(\beta_1 = 3\), то коли \(x_1\) дорівнює км, \(\beta_1 = 3000\).
Шкала/одиниці предикторів не впливають на оцінки методом найменших квадратів.

Ridge regression сплачує набагато більший штраф за \(\beta_1=3000\), ніж \(\beta_1=3\).
Ви не отримаєте однакові (масштабовані) оцінки, змінюючи одиниці вимірювання.

Рішення Стандартизуйте свої змінні, тобто,
x_stnd = (x - середнє (x))/sd(x).

Штрафи та стандартизація

Значення предикторів можуть мати суттєвий вплив на результат рідж регресії

Чому?

Тому що значення \(\mathbf{x}_j\) впливають на \(\beta_j\), а ridge дуже чутливий до \(\beta_j\).

Приклад Нехай \(x_1\) це відстань.

МНК
Якщо \(x_1\) вимірюється метрами і \(\beta_1 = 3\), то коли \(x_1\) дорівнює км, \(\beta_1 = 3000\).
Шкала/одиниці предикторів не впливають на оцінки методом найменших квадратів.

Ridge regression сплачує набагато більший штраф за \(\beta_1=3000\), ніж \(\beta_1=3\).
Ви не отримаєте однакові (масштабовані) оцінки, змінюючи одиниці вимірювання.

Рішення Стандартизуйте свої змінні, тобто,
recipes::step_normalize().

Приклад

Повернемося до набору кредитних даних і попередньої обробки за допомогою tidymodels.

У нас є 11 предикторів і числовий результат “баланс”.

Ми можемо стандартизувати наші предиктори за допомогою step_normalize() з recipes:

# Load the credit dataset
credit_df = ISLR::Credit %>% clean_names()
# Processing recipe: Define ID, standardize, create dummies, rename (lowercase)
credit_recipe = credit_df %>% recipe(balance ~ .) %>% 
  update_role(id, new_role = "id variable") %>% 
  step_normalize(all_predictors() & all_numeric()) %>% 
  step_dummy(all_predictors() & all_nominal()) %>% 
  step_rename_at(everything(), fn = str_to_lower)
# Time to juice
credit_clean = credit_recipe %>% prep() %>% juice()

Приклад

Для ridge regression в R ми будемо використовувати glmnet() з пакета glmnet.

Основними аргументами glmnet() є

  • x матриця предикторів
  • y змінна результату як вектор
  • standardize (T або F)
  • параметр alpha elasticnet
    • alpha=0 дає ridge
    • alpha=1 дає lasso
  • параметр lambda гіперпараметр
  • nlambda альтернативно, R вибирає послідовність значень для λ

Приклад

Нам просто потрібно визначити спадаючу послідовність для \(\lambda\).

# Define our range of lambdas (glmnet wants decreasing range)
lambdas = 10^seq(from = 5, to = -2, length = 100)
# Fit ridge regression
est_ridge = glmnet(
  x = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix(),
  y = credit_clean$balance,
  standardize = F,
  alpha = 0,
  lambda = lambdas
)

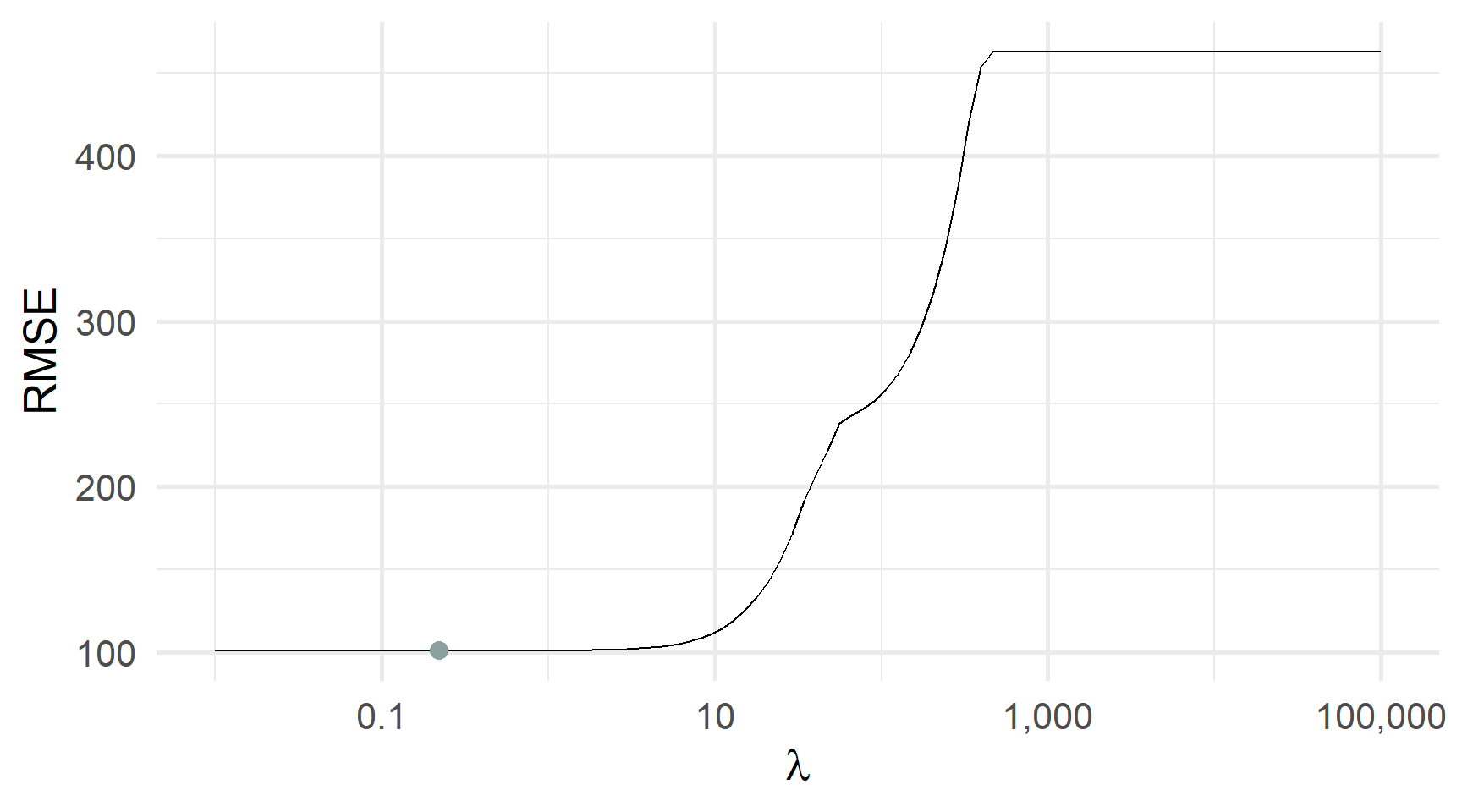
Вихід glmnet (тут est_ridge) містить оцінені коефіцієнти для \(\lambda\). Ви можете використовувати predict(), щоб отримати коефіцієнти для додаткових значень \(\lambda\).

Коефіцієнти Ridge регресії для λ від 0,01 до 100 000

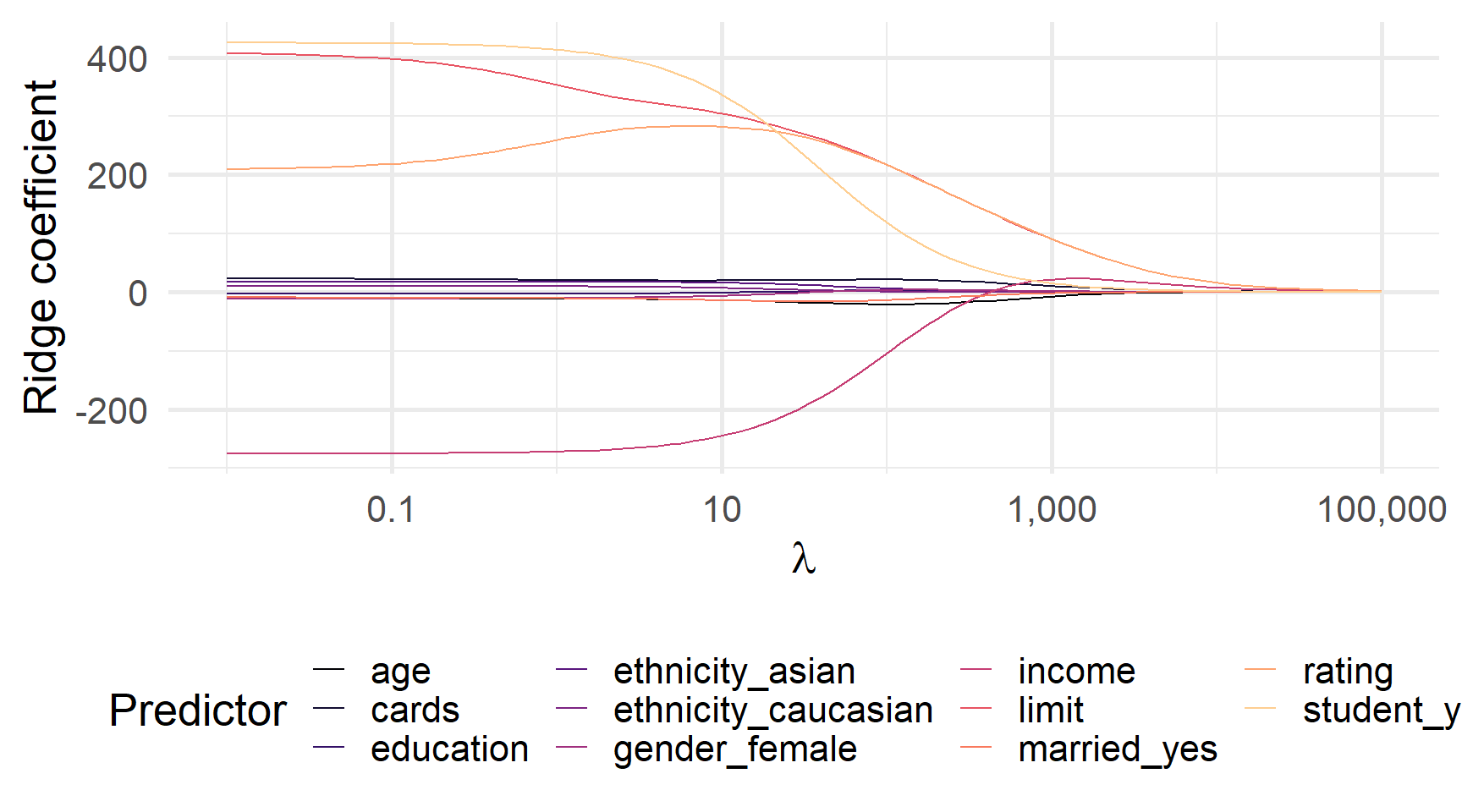
Приклад

glmnet також надає зручну функцію перехресної перевірки: cv.glmnet().

# Define our lambdas
lambdas = 10^seq(from = 5, to = -2, length = 100)
# Cross validation
ridge_cv = cv.glmnet(
  x = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix(),
  y = credit_clean$balance,
  alpha = 0,
  standardize = F,
  lambda = lambdas,
  # New: How we make decisions and number of folds
  type.measure = "mse",
  nfolds = 5
)

Перехресна перевірка RMSE і λ: Яка λ мінімізує CV RMSE?

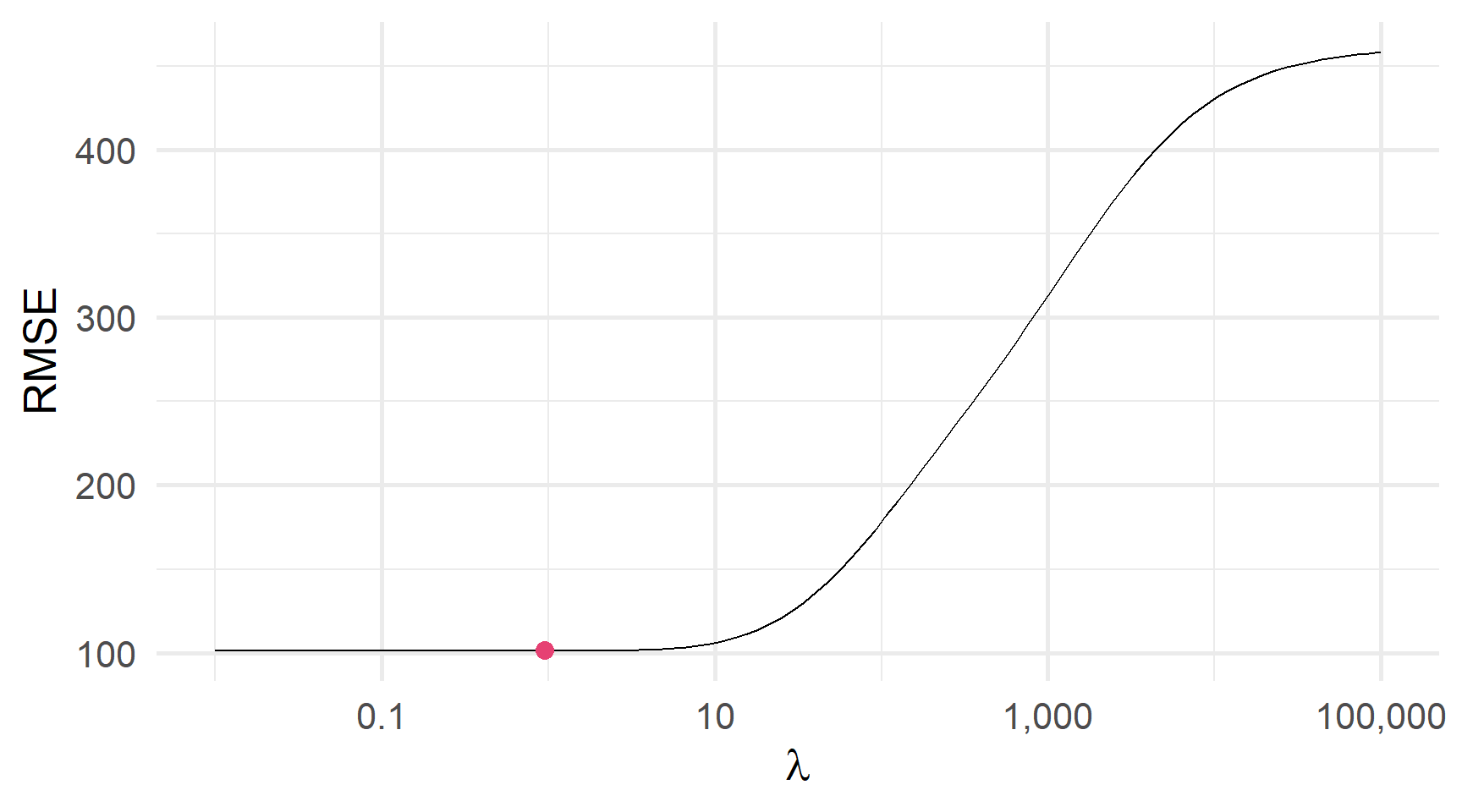
Але інколи мінімум буде більш явний

Перехресна перевірка RMSE і λ: Яка λ мінімізує CV RMSE?

У tidymodels

tidymodels також може провести перехресну перевірку (і підібрати) ridge регресію.

  • Повернемося до нашої «специфікації» моделі linear_reg().

  • Пенальті \(\lambda\) (те, що ми хочемо налаштувати) є penalty замість lambda.

  • Встановіть mixture = 0 всередині linear_reg() (те саме, що alpha = 0 вище).

  • Використовуйте двигун glmnet.

# Define the model
model_ridge = linear_reg(penalty = tune(), mixture = 0) %>% set_engine("glmnet")

Приклад ridge регресії з tidymodels

# Our range of lambdas
lambdas = 10^seq(from = 5, to = -2, length = 1e3)
# Define the 5-fold split
set.seed(12345)
credit_cv = credit_df %>% vfold_cv(v = 5)
# Define the model
model_ridge = linear_reg(penalty = tune(), mixture = 0) %>% set_engine("glmnet")
# Define our ridge workflow
workflow_ridge = workflow() %>%
  add_model(model_ridge) %>% add_recipe(credit_recipe)
# CV with our range of lambdas
cv_ridge = 
  workflow_ridge %>%
  tune_grid(
    credit_cv,
    grid = data.frame(penalty = lambdas),
    metrics = metric_set(rmse)
  )
# Show the best models
cv_ridge %>% show_best()

З tidymodels…
Завершіть робочий процес і оцініть свою останню модель.
finalize_workflow(), last_fit() та collect_predictions()

Прогнози в R

Коли ви знайдете \(\lambda\) через перехресну перевірку,

1. Fit свою модель до повного набору даних за допомогою оптимального \(\lambda\)

# Fit final model
final_ridge =  glmnet(
  x = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix(),
  y = credit_clean$balance,
  standardize = T,
  alpha = 0,
  lambda = ridge_cv$lambda.min
)

Прогнози в R

Коли ви знайдете \(\lambda\) через перехресну перевірку,

1. Fit свою модель до повного набору даних за допомогою оптимального \(\lambda\)
2. Робіть прогнози

predict(
  final_ridge,
  type = "response",
  # Our chosen lambda
  s = ridge_cv$lambda.min,
  # Our data
  newx = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix()
)

Стиснення

Хоча ridge регресія штрафує коефіцієнти, і наближає їх до нуля, вона ніколи зводить їх до абсолютного нуля.

Недоліки

  1. Ми не можемо використовувати ridge регресію для вибору підмножини/фічей
  2. Ми часто отримуємо купу малих коефіцієнтів.

Чи можемо ми просто обнулити коефіцієнти?

Так. Тільки не з ridge (через \(\sum_j \hat{\beta}_j^2\)).

Lasso

Lasso

Lasso просто замінює квадрат коефіцієнтів ridge регресії на абсолютні значення.

Ridge regression \[ \begin{align} \min_{\hat{\beta}^R} \sum_{i=1}^{n} \big( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \big)^2 + \color{#e64173}{\lambda \sum_{j=1}^{p} \beta_j^2} \end{align} \] Lasso \[ \begin{align} \min_{\hat{\beta}^L} \sum_{i=1}^{n} \big( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \big)^2 + \color{#8AA19E}{\lambda \sum_{j=1}^{p} \big|\beta_j\big|} \end{align} \]

Все інше буде таким же, крім одного аспекту…

Стиснення

На відміну від Ridge, штраф Lasso не збільшується з розміром \(\beta_j\)

Ця функція має дві переваги

  1. Деякі коефіцієнти будуть дорівнювати нулю — ми отримуємо «розріджені» моделі.
  2. Ласо можна використовувати для вибору підмножини/фічей.

Нам все одно треба уважно вибрати \(\color{#8AA19E}{\lambda}\).

Приклад

Ми також можемо використовувати glmnet() для лассо.

Ключові аргументи для glmnet() є

  • x матриця предикторів
  • y вихід моделі як вектор
  • standardize (T або F)
  • параметр elasticnet alpha
    • alpha=0 дає ridge
    • alpha=1 дає lasso
  • lambda: гіперпараметр
  • nlambda альтернативно, R вибирає послідовність значень для \(\lambda\)

Приклад

Знову ж таки, ми визначаємо спадаючу послідовність для \(\lambda\)…

# Define our range of lambdas (glmnet wants decreasing range)
lambdas = 10^seq(from = 5, to = -2, length = 100)
# Fit lasso regression
est_lasso = glmnet(
  x = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix(),
  y = credit_clean$balance,
  standardize = F,
  `alpha = 1`,
  lambda = lambdas
)

Вихід glmnet (тут est_lasso) містить оцінені коефіцієнти для \(\lambda\). Ви можете використовувати predict(), щоб отримати коефіцієнти для додаткових значень \(\lambda\).

Коефіцієнти ласо для \(\lambda\) від 0,01 до 100 000

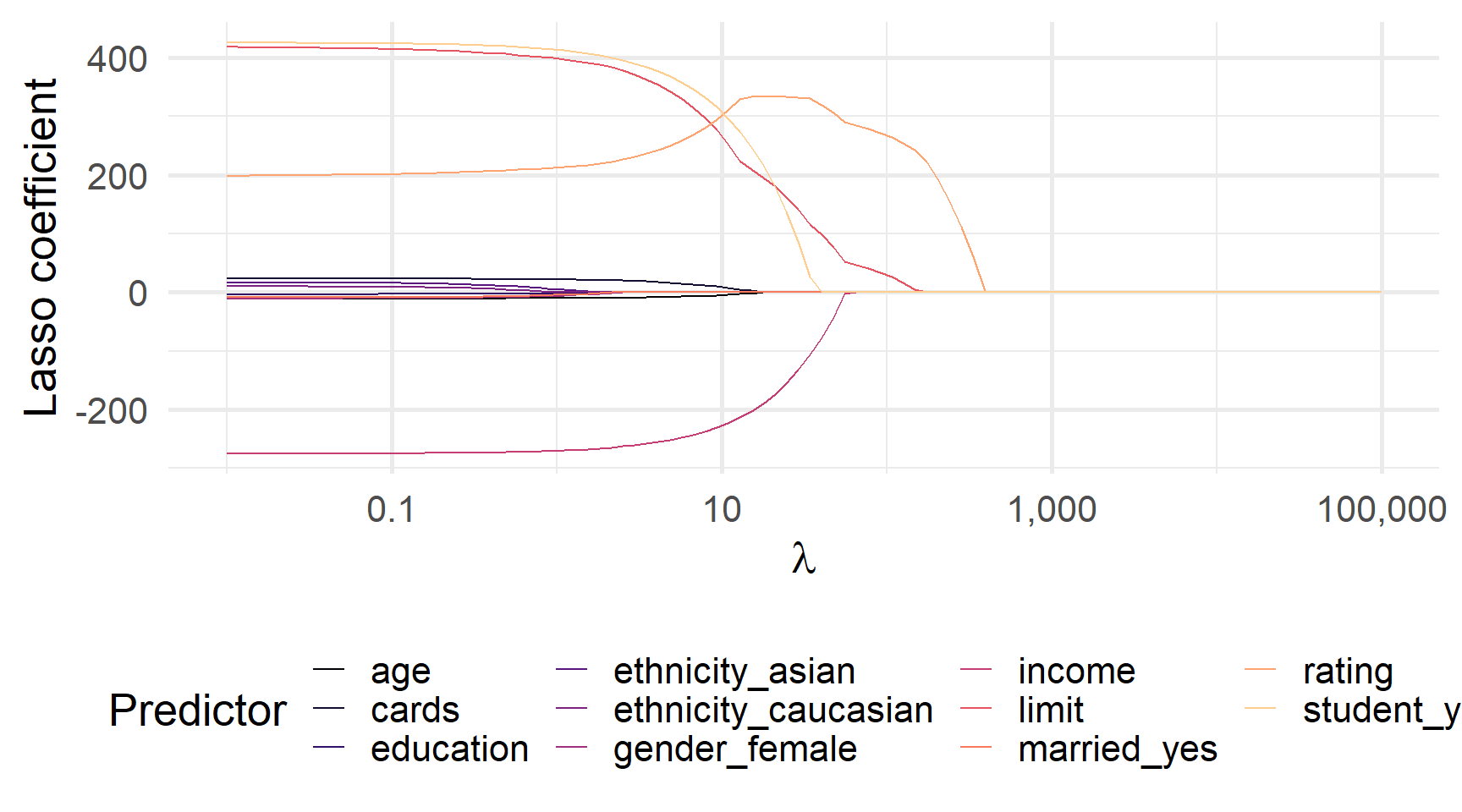
Приклад

Ми також можемо перехресно перевірити \(\lambda\) за допомогою cv.glmnet().

# Define our lambdas
lambdas = 10^seq(from = 5, to = -2, length = 100)
# Cross validation
lasso_cv = cv.glmnet(
  x = credit_clean %>% dplyr::select(-balance, -id) %>% as.matrix(),
  y = credit_clean$balance,
  alpha = 1,
  standardize = F,
  lambda = lambdas,
  # New: How we make decisions and number of folds
  type.measure = "mse",
  nfolds = 5
)

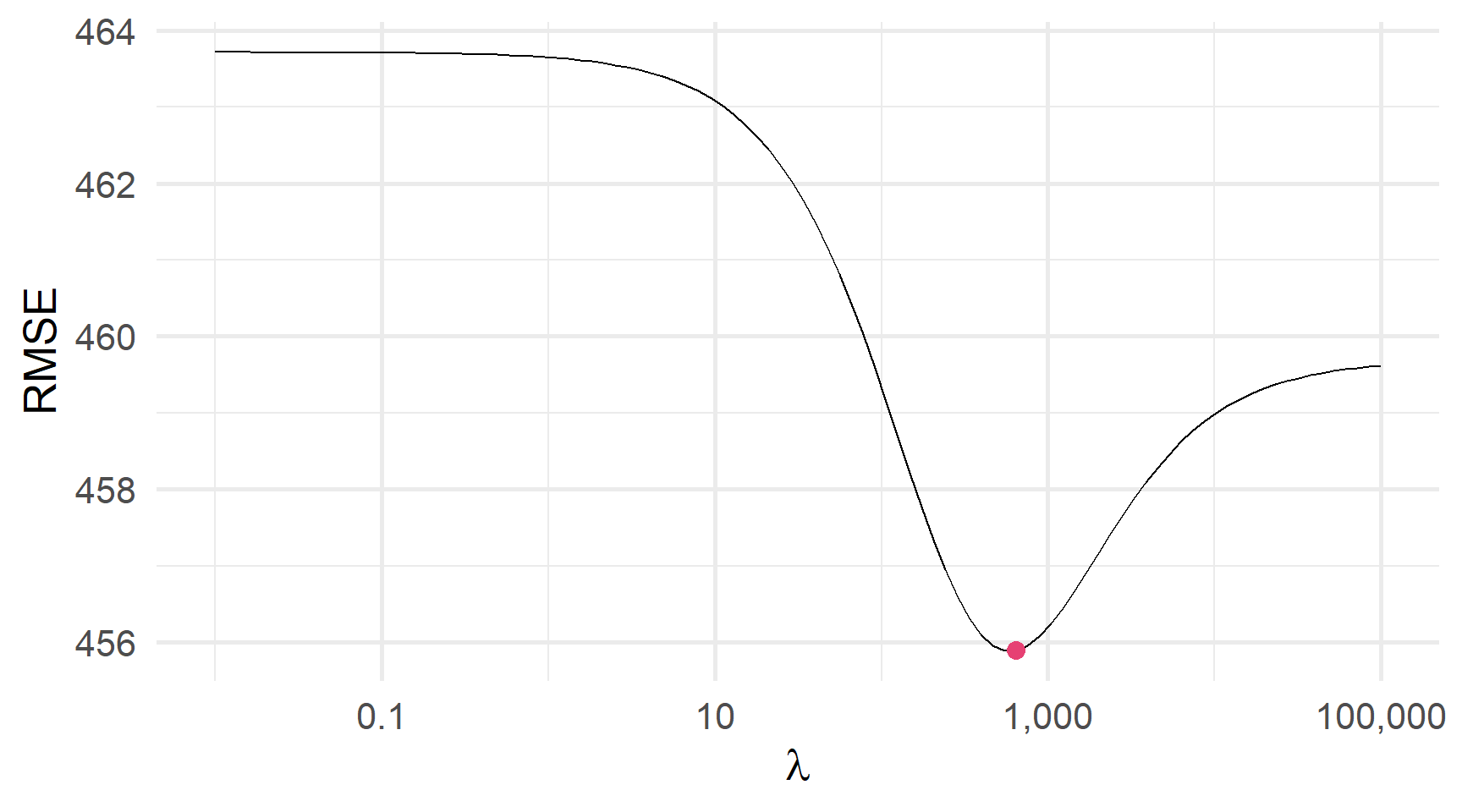
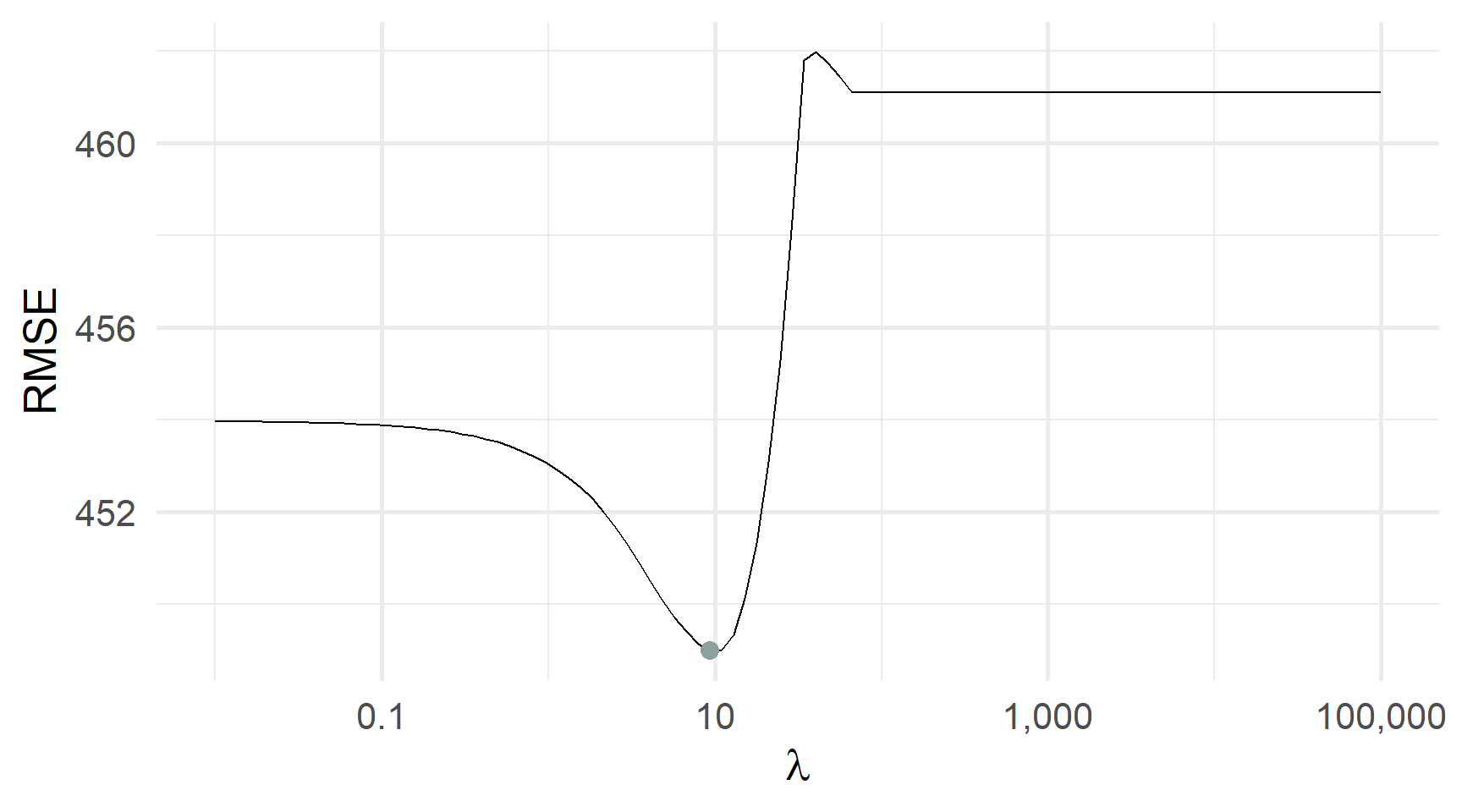
Перехресна перевірка RMSE та λ: який λ мінімізує CV RMSE?

І знову мінімум може бути більш явний

Перехресна перевірка RMSE та λ: який λ мінімізує CV RMSE?

Який метод використовувати?

Ridge чи lasso?

Ridge regression
[+] зменшує \(\hat{\beta}_j\) близько до 0
[-] багато маленьких \(\hat\beta_j\)
[-] не працює для формування підвибірки
[-] важко інтерпретувати вихід моделі
[+] краще, коли всі \(\beta_j\neq\) 0

Best: \(p\) великий & \(\beta_j\approx\beta_k\)

Lasso


[+] зменшує \(\hat{\beta}_j\) до 0
[+] багато \(\hat\beta_j=\) 0
[+] підходить для підвибірки
[+] розріджені моделі легше інтерпретувати
[-] неявно передбачає деяке \(\beta=\) 0

Best: \(p\) великий і багато \(\beta_j\approx\) 0

Ні ridge… а ні lasso не домінують над іншими моделями.

Ridge та lasso?
Elasticnet поєднує Ridge та lasso.

Elasticnet

Elasticnet

Elasticnet** поєднує Ridge та lasso.

\[ \begin{align} \min_{\beta^E} \sum_{i=1}^{n} \big( \color{#FFA500}{y_i} - \color{#6A5ACD}{\hat{y}_i} \big)^2 + \color{#181485}{(1-\alpha)} \color{#e64173}{\lambda \sum_{j=1}^{p} \beta_j^2} + \color{#181485}{\alpha} \color{#8AA19E}{\lambda \sum_{j=1}^{p} \big|\beta_j\big|} \end{align} \]

Тепер у нас є два параметри налаштування: \(\lambda\) (penalty) і \(\color{#181485}{\alpha}\) (mixture).

Пам’ятаєте аргумент alpha в glmnet()?

  • \(\color{#e64173}{\alpha = 0}\) визначає Ridge
  • \(\color{#8AA19E}{\alpha=1}\) визначає lasso.

Ridge та lasso?

Ми можемо використовувати tune() з tidymodel для перехресної перевірки як \(\alpha\), так і \(\lambda\).

Потрібно враховувати всі комбінації двох параметрів.
Ця комбінація може створити багато моделей для оцінки.

Наприклад, - 1000 значень \(\lambda\) - 1000 значень \(\alpha\)

залишає вам 1 000 000 моделей для оцінки

Cross validating elasticnet у tidymodels

# Our range of λ and α
lambdas = 10^seq(from = 5, to = -2, length = 1e2)
alphas = seq(from = 0, to = 1, by = 0.1)
# Define the 5-fold split
set.seed(12345)
credit_cv = credit_df %>% vfold_cv(v = 5)
# Define the elasticnet model
model_net = linear_reg(
  penalty = tune(), mixture = tune()
) %>% set_engine("glmnet")
# Define our workflow
workflow_net = workflow() %>%
  add_model(model_net) %>% add_recipe(credit_recipe)
# CV elasticnet with our range of lambdas
cv_net = 
  workflow_net %>%
  tune_grid(
    credit_cv,
    grid = expand_grid(mixture = alphas, penalty = lambdas),
    metrics = metric_set(rmse)
  )

Cross validating elasticnet у tidymodels з grid_regular()

# Our range of λ and α
lambdas = 10^seq(from = 5, to = -2, length = 1e2)
alphas = seq(from = 0, to = 1, by = 0.1)
# Define the 5-fold split
set.seed(12345)
credit_cv = credit_df %>% vfold_cv(v = 5)
# Define the elasticnet model
model_net = linear_reg(
  penalty = tune(), mixture = tune()
) %>% set_engine("glmnet")
# Define our workflow
workflow_net = workflow() %>%
  add_model(model_net) %>% add_recipe(credit_recipe)
# CV elasticnet with our range of lambdas
cv_net = 
  workflow_net %>%
  tune_grid(
    credit_cv,
    grid = grid_regular(mixture(), penalty(), levels = 100:100),
    metrics = metric_set(rmse)
  )

Краща модель мала \(\lambda\approx\) 0,628 і \(\alpha\approx\) 0,737.
CV з elasticnet зменшив RMSE з 118 до 101.

Дякую за увагу!



Data Mirosh

@aranaur

ihor.miroshnychenko@kneu.ua

@ihormiroshnychenko

aranaur.rbind.io